Уровень в I резервуаре считаем постоянным. Свяжем уравнением Бернулли сечения 1-1 и К-К, располагая их на уровнях свободной поверхности в I и II резервуаре соответственно, проведя линию сравнения по уровню свободной поверхности в первом резервуаре и считая равной 0 скорость в первом сечении.
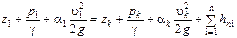 , (2)
, (2)
где 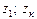 – ординаты, определяющие высоту положения центра выбранного сечения над горизонтальной плоскостью сравнения 0–0;
– ординаты, определяющие высоту положения центра выбранного сечения над горизонтальной плоскостью сравнения 0–0;
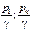 – пьезометрический напор в сечениях 1–1 и К–К;
– пьезометрический напор в сечениях 1–1 и К–К;
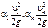 – скоростной напор в сечениях 1–1 и К–К;
– скоростной напор в сечениях 1–1 и К–К;
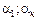 – коэффициенты Кориолиса, учитывающие неравномерность распределения скоростей в соответствующих живых сечениях потока;
– коэффициенты Кориолиса, учитывающие неравномерность распределения скоростей в соответствующих живых сечениях потока;
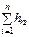 – сумма потерь напора.
– сумма потерь напора.
После решения уравнения, получим
hдейств.= hм + h l , (3)
где 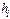 – потери напора по длине;
– потери напора по длине;
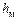 – местные потери.
– местные потери.
Потери напора по длине рассчитываются по формуле Дарси-Вейсбаха:
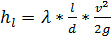 , (4)
, (4)
где λ – коэффициент гидравлического трения;
l – длина трубопровода;
d – внутренний диаметр трубопровода;
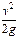 – скоростной напор в рассматриваемом участке трубопровода,
– скоростной напор в рассматриваемом участке трубопровода,
g – ускорение свободного падения, g = 9,81 м/с2.
Коэффициент гидравлического трения λ зависит от числа Рейнольдса Re и относительной шероховатости Δэ/d, где Δэ – эквивалентная
шероховатость. По таблице А3 (ПРИЛОЖЕНИЕ А) для заданного материала трубопровода выбираем Δэ, мм.
Число Рейнольдса определяется по формуле
R_е=(V_ф∙d_ф)/ν , (5)
где ν – кинематический коэффициент вязкости. Для воды при t = 20 ºC ν=0,0101 〖см〗^2/с=0,101·〖10〗^(-5) м^2/с. ( таблица А1, ПРИЛОЖЕНИЕ А)
Местные потери напора определяются по формуле Вейсбаха
h_м=ζ*〖v/2g〗^2=(〖 ζ〗_фильтра+ζ_(〖90〗^о )+ζ_(〖90〗^о )+〖 ζ〗_выхода ) 〖v/2g〗^2, (6)
Где 〖 ζ〗_фильтра,ζ_(〖90〗^о ),ζ_(〖90〗^о ),〖 ζ〗_выхода – коэффициенты местных сопротивлений, соответственно на входе трубы, повороте трубопровода на 90֯ и выходе трубы.
Расчет перепада уровней в I и II резервуаре дает возможность установить действительный перепад уровней hдейств., который отличен от заданного h1 и соответствует выбранному диаметру сифона
При заданном расходе Q= 63 л/с и гидравлическом уклоне iср= 0.021 по справочнику [1] определяем фактический диаметр, который равен dф=0.25м.
Зная диаметр можем рассчитать скорость в трубопроводе:
V_ф= 4Q/(π∙〖d_ф〗^2 ) , (7)
V_ф= (4*63*〖10〗^(-3))/(π∙〖0,25〗^2 )=1,284 м/с.
Определим число Рейнольдса по формуле (3):
R_е=(1,284*0,25)/(0,101*〖10〗^(-5) )=3,18*〖10〗^5,
Определим режим движения жидкости по трубопроводу. Полученные значения числа Рейнольдса трубопровода больше критического значения числа Рейнольдса, значит режим движения турбулентный.
лам.<2320<турб.
Для турбулентного режима движения, когда число Рейнольдса Re>105 коэффициент Дарси рассчитывается по формуле Шипринсона[3]:
λ=0,11∙∜(Δэ/d_ф ) , (8)
где Δэ - эквивалентная абсолютная шероховатость, м [1]
λ=0,11∙∜((0,1∙〖10〗^(-3))/0,25)=0,016.
3.Определение потерь напора в трубопроводе
Потери в трубопроводе можно определить уравнением
∑ hw = hм + hl =(λ∙l/d_ф +〖 ζ〗_фильтра+ζ_(〖90〗^о )+ζ_(〖90〗^о )+〖 ζ〗_выхода)∙〖V_ф〗^2/(2∙g) , (9)
∑ hw = hм + hl =(0,016∙20/0,25 +3+0,2+0,2+0,5)∙〖1,284〗^2/(2∙9,81)=1,19м.
Теперь по условию необходимо проверить возможность подъема воды в сифоне на заданную высоту h0. Уровень в I резервуаре считаем постоянным. Свяжем уравнением Бернулли сечения 1-1 и М-М, располагая их на уровнях свободной поверхности в I и на высоте h0 соответственно, проведя линию сравнения по уровню свободной поверхности в первом резервуаре и считая равной 0 скорость в первом сечении. Тогда уравнение (2) примет вид:
р_а/(ρ*g)= h_0+р_вак/(ρ*g)+(α+ζ_фильтра+ζ_(90֯)+λ*l_1/d_ф )*〖V_ф〗^2/(2∙g), (10)
h_0=р_а/(ρ*g)-р_вак/(ρ*g)-(α+ζ_фильтра+ζ_(90֯)+λ*l_1/d_ф )*〖V_ф〗^2/(2∙g),
h_0=〖10〗^5/(1000*9,81)-(0,1*〖10〗^5)/(1000*9,81)-(1+3+0,2+0,016*10/0,25)*〖1,284〗^2/(2∙9,81)=8,76 м.
По условию h_0=4 м, тем самым можно сделать вывод, что поднятие на высоту 4 м метра возможно.
4.Определение диаметра всасывающего трубопровода насосной установки
Диаметр всасывающего трубопровода насоса dвс. по заданию принимаем равным dвс.=0.3 м. Считаем поток воды из прибрежного резервуара I до напорного резервуара III непрерывным, т.е. во всех напорных трубопроводах системы Q = const.
5.Определение высоты установки центра насоса над линией свободной поверхности
Для определения высоты расположения центра насоса над линией свободной поверхности во II резервуаре h2 = hвс. свяжем уравнением Бернулли сечения 1-1 и 2-2, расположенные по линии свободной поверхности в резервуаре и на входе всасывающего трубопровода в насос.
Далее рассмотрим местные сопротивления во всасывающем трубопроводе. К ним можно отнести два поворота трубопровода на 900, сопротивление сетки фильтра.
Решим уравнение относительно искомого значения высоты установки центра насоса над линией свободной поверхности hвс.
h_вс=(p_а-p_вак)/γ-〖V_вс〗^2/(2∙g)-(λ∙l_вс/d_вс +ζ_сетки+ζ_(〖90〗^о )+ζ_(〖90〗^о ))∙〖V_вс〗^2/(2∙g), (11)
где ра=105Па-нормальное атмосферное давление, рвак=0.1*105Па (по заданию).
Скорость во всасывающем трубопроводе определим по формуле:
V_вс= 4Q/(π∙〖d_вс〗^2 )=(4*63*〖10〗^(-3))/(π*〖0,3〗^2 )=0,89м/с.
Теперь определим режим движения по формуле (5):
R_е=(0,89*0,3)/(0,101*〖10〗^(-5) )=2,6*〖10〗^5.
Следовательно, режим турбулентный(лам.<2320<турб).
Для турбулентного режима движения коэффициент Дарси определяется по формуле Шипринсона(8):
λ=0,11∙∜((0,1∙〖10〗^(-3))/0,3)=0,015.
Для отводов круглого сечения с углом поворота δ= 900 и R/d 1 при турбулентном течении можно воспользоваться эмпирической формулой:
ζ_(〖90〗^о )=0,051+(0,19*d)/R, (12)
где R/d это отношение радиуса поворота к диаметру трубы и по условию R/ dвс =6,0.
Тогда
ζ_(〖90〗^о )=0,051+(0,19*1)/6=0,11.
Теперь определим h_вс :
h_вс=(〖0,8*10〗^5-〖0.1*10〗^5)/(1000*9.81)-〖0.89〗^2/(2∙9.81)-(0.015∙47/0.3+3+0.11+0.11)∙〖0.89〗^2/(2∙9.81)=8,91м.
Определение высоты установки центра насоса над линией свободной поверхности позволяет определить геометрический напор, который является расстоянием от уровня свободной поверхности в резервуаре I до уровня свободной поверхности в резервуаре III.
Hг = hвс. + H, (13)
Нг=8,91+19=27.91 м.
6. Определение потерь напора во всасывающем трубопроводе
Потери во всасывающем трубопроводе при турбулентном движении жидкости можно определить уравнением :
∑h_вс=(λ∙l_вс/d_вс +ζ_фильтра+ζ_(〖90〗^о )+ζ_(〖90〗^о ))∙〖V_вс〗^2/(2∙g) , (14)
∑h_вс=(0.017∙47/0.3+3+0.11+0.11)∙〖0.89〗^2/(2∙9.81)=0,61 м.
7.Определение диаметра нагнетательного трубопровода насосной установки
При выборе диаметра нагнетательного трубопровода dн допускается соотношение
dвс.≥dн. (15)
Принимаем dн=0.25 м( по заданию).
8. Определение потерь напора в нагнетательном трубопроводе
Нагнетательный трубопровод – длинный трубопровод. Скорость движения жидкости в нагнетательном трубопроводе
〖 V〗_н= 4Q/(π∙〖d_н〗^2 ) , (16)
V_н= 4Q/(π∙〖d_н〗^2 )=(4*63*〖10〗^(-3))/(π*〖0,25〗^2 )=1,284м/с.
Число Рейнольдса для нагнетательного трубопровода и определим режим движения жидкости в нем
〖 R〗_е=(V_н∙d_н)/ν , (17)
R_е=(1,284*0,25)/(0,101*〖10〗^(-5) )=3,18*〖10〗^5.
Определим режим движения жидкости по трубопроводу. Полученные значения числа Рейнольдса трубопровода больше критического значения числа Рейнольдса, значит режим движения турбулентный.
лам.<2320<турб.
Для турбулентного режима движения коэффициент Дарси определяется по формуле (8):
λ=0,11∙∜((0,1∙〖10〗^(-3))/0,25)=0,016.
Для длинного нагнетательного трубопровода производим расчет потерь по длине для диаметра напорного трубопровода dн и длины lн. Далее рассмотрим местные сопротивления в нагнетательном трубопроводе, которые представляют собой потери по длине и потери на местные сопротивления h_(м.н)., которые составляют около 10% от потерь по длине hl в длинном трубопроводе. Тогда общие потери в напорном трубопроводе определим, согласно уравнению:
∑h_н=(λ∙l_1/d_н +ζ_выхода+ζ_(〖90〗^о ))∙〖V_н〗^2/(2∙g) , (18)
∑h_н=(0.016∙115/0.25+0.2)∙〖1.284〗^2/(2∙9.81)=0,72 м.
9.Определение потребного напора насосной установки
Потребным напором насосной установки называется энергия, необходимая для перемещения единицы веса жидкости от самого нижнего уровня (в месте забора) до самого верхнего (центра тяжести выходного сечения или верхнего уровня в приемном резервуаре). Потребный напор определяется по формуле
Нпотр. = Нст +Н дин. , (19)
где– Нст статический напор, учитывающий затраты энергии для подъема жидкости на высоту Hг (формула 1.23) и потерь на преодоление перепада давлений ра и р0 на линиях поверхности жидкости в I и III резервуарах соответственно (для варианта задания А ра =р0) ;
Нст = Hг + (р0 - ра)/ ρ•g , (20)
где Н дин. – гидравлические потери, учитывающие потери в местных сопротивлениях и потери напора по длине.
Нст =27,91 + (2*〖10〗^5-〖10〗^5)/(1000*9,81)=16,19 м.
Так как диаметры всасывающего и нагнетательного трубопровода не одинаковы, то
Н дин. =(ϑ_вс^2+ϑ_(н )^2)/(2*g) +∑h_вс+∑h_н = (〖1,284〗^2+〖0,89〗^2)/(2*9,81) + 0,61 + 0,72= 3,46 м ; (21)
Нпотр. = 16,19 +3,46=19,64 м.
10.Определение разности горизонтов в резервуарах III и IV
Указанную разность можно вычислить из формулы для определения расхода жидкости:
Q=μω√(2gh_3 ), (22)
где Q-расход жидкости, проходящий из резервуара III в резервуар IV, равный производительности насоса;
μ-коэффициент расхода (для истечения под уровень μ=0,62);
ω-площадь поперечного сечения;
g-ускорение силы тяжести;
h_3-разность уровней в резервуарах.
Из формулы (19) получим:
ω=(π〖d_отв〗^2)/4= (π*〖0,063〗^2)/4=0,0031м2 (23)
h_3=Q^2/((〖μω)〗^2*2g)= 〖〖(63*10〗^(-3))〗^2/(〖(0,62*0,0031)〗^2*2*9,81)=1,26м. (24)
11. Определение мощности насосной установки
Различают полезную мощность Np ,кВт, которая определяется работой насоса, совершаемой им при подъеме жидкости в единицу времени на высоту Н и мощность, необходимая для приведения в действие насосной установки Nуст.
Np=(ρ*g*Q*H_потр)/1000=(1000*9,81*63*〖10〗^(-3)*19,64)/1000=12,14кВт. (25)
Список литературы
1. Киселев П.Г. Справочник по гидравлическим расчетам. Л.: 1961. – 352 с.
2. Шевелев Ф.А., Шевелева А.Ф. Таблицы гидравлического расчета водопроводных труб. М.: Стройиздат, 1984. -112 с.
СПИСОК ЛИТЕРАТУРЫ
1 Киселев П.Г. Справочник по гидравлическим расчетам. Л.: 1961. – 352 с.
2 Шевелев Ф.А., Шевелева А.Ф. Таблицы гидравлического расчета водопроводных труб. М.: Стройиздат, 1984. -112 с.
Приложение А
Таблица А.1 – Зависимость коэффициента кинематической вязкости воды от температуры
| t, ºC | 0 | 5 | 7 | 10 | 12 |
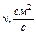
| 0,0179 | 0,0152 | 0,0143 | 0,0131 | 0,0124 |
| t, ºC | 15 | 17 | 20 | 25 | 30 |
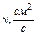
| 0,0114 | 0,0109 | 0,0101 | 0,009 | 0,008 |
Таблица А.2 - Коэффициенты местных сопротивлений
| Наименование вида местного сопротивления | Коэффициент местного сопротивления 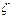
|
| Вентиль с изменением направления движения жидкости на 900 Вентиль с прямоточным движением жидкости Распределительные устройства и обратные клапаны Значительное расширение потока при поступлении жидкости в гидроцилиндры Штампованные или сверленые угольники под 900 Прямоугольные тройники: для отводимого под углом 900 потока для транзитного потока Выход жидкости из цилиндров в трубы Приемный клапан Кран управления (при угле поворота 50) Фильтр Закругление трубы под 900 |
2,5 – 3
0,5 – 1
2 – 3
0,8 – 0,9
2
1 – 1,2
0,1 – 0,2
0,5
10
0,05
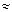 12
0,15 – 0,25 12
0,15 – 0,25
|
Таблица А.3 - Эквивалентная шероховатость для труб из различного материала
| Материал трубопровода | Эквивалентная шероховатость 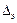 , мм , мм
|
| Стекло | 0 |
| Трубы, тянутые из латуни, свинца, меди | 0…0,002 |
| Высококачественные бесшовные стальные трубы | 0,06…0,2 |
| Стальные трубы | 0,1…0,5 |
| Чугунные асфальтированные трубы | 0,1…0,2 |
| Чугунные трубы | 0,2…1,0 |
Таблица А 4 – Значения коэффициента гидравлического трения и модуля расхода для круглых труб, рассчитанные по формуле Павловского Н.Н. при коэффициенте шероховатости n = 0,012
| d, мм | 50 | 75 | 100 | 150 | 200 | 250 | 300 | 350 | 400 |
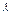
| 0,0391 | 0,0349 | 0,0321 | 0,0286 | 0,0263 | 0,0247 | 0,0334 | 0,0224 | 0,0216 |
| К, м3/с | 0,0098 | 0,0287 | 0,0614 | 0,1794 | 0.3837 | 0.6921 | 1.1206 | 1.6842 | 2.3970 |
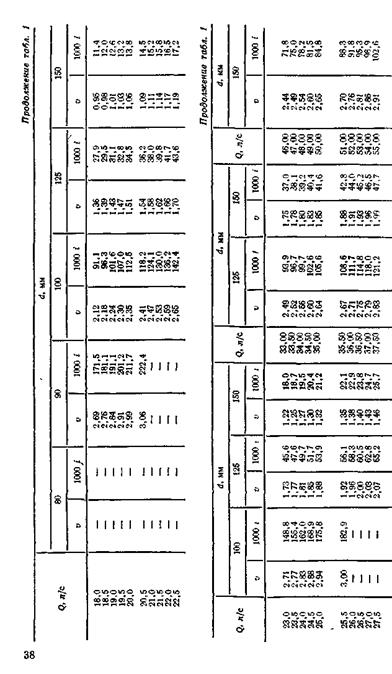
Таблица А 5 – Таблица для гидравлического расчета водопроводных труб [2]
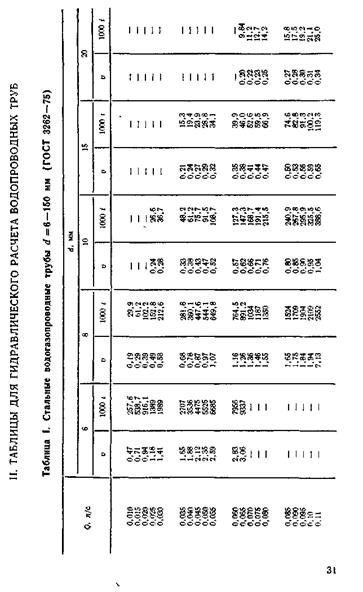
1. 
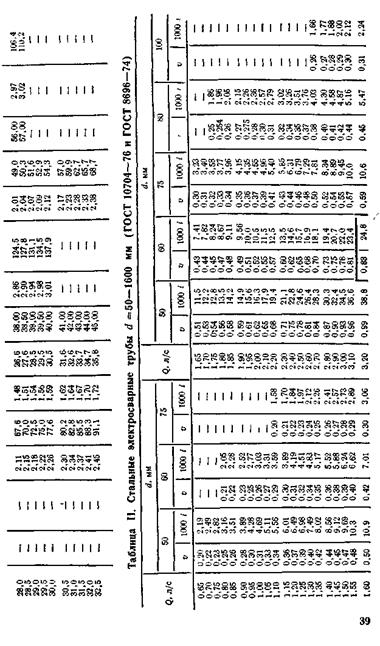

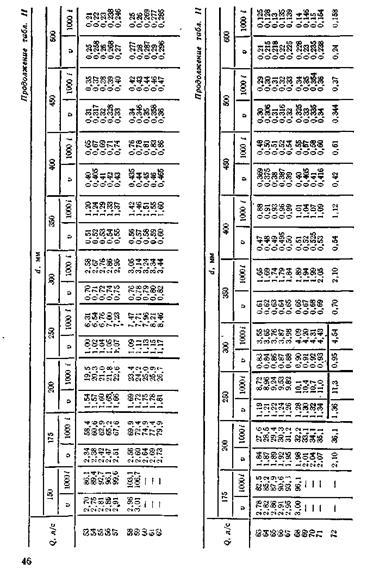

ПРИЛОЖЕНИЕ Б
Образец оформления титульного листа к расчетно-графической работе № 1
| Министерство транспорта и коммуникаций Республики Беларусь Белорусский государственный университет транспорта Кафедра «Экология и энергоэффективность в техносфере» Расчетно-графическая работа №1 «Гидравлический расчет напорного трубопровода в системе водоснабжения» по дисциплине «Механика жидкости и газа» для специальности 1-70 04 03 Водоснабжение, водоотведение и охрана водных ресурсов Выполнил студент Принял преподаватель группы СВ – 21 к.т.н., доцент Вострова Р.Н. Иванов А.П. Учебный шифр Гомель 2017 |
Дата: 2018-11-18, просмотров: 558.