Вологда
2018
Введение
Данное учебно-методическое пособие предназначено для студентов заочной и заочной ускоренной формы обучения по направлению подготовки электроэнергетика и электротехника, профиль: электроснабжение. Текст содержит варианты трех контрольных работ, которые необходимо самостоятельно выполнить студентам в первом семестре, разбор задач, аналогичных предложенным в контрольных работах. Кроме того, в пособии приведен справочный теоретический материал, необходимый для выполнения контрольных заданий. Номер варианта контрольной работы определяется в соответствии с последней цифрой шифра студента – номера его зачетной книжки. Каждая работа выполняется в отдельной тетради, задачи должны быть представлены в том порядке, в котором они указаны в контрольной работе. Компьютерное оформление работ на проверку не принимается.
Задачи для контрольных заданий
Контрольная работа № 1
Тема 1. Комплексные числа.
Тема 2. Основные понятия линейной алгебры.
Задача 1. Найти: а) область определения функции 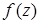 ;
;
б) значение функции 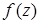 в точке
в точке 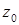 .
.
1.1. 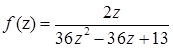 ,
, 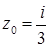 .
.
1.2. 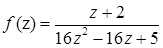 ,
, 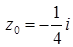 .
.
1.3. 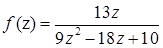 ,
, 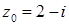 .
.
1.4. 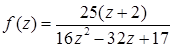 ,
, 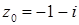 .
.
1.5. 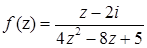 ,
, 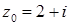 .
.
1.6. 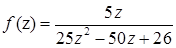 ,
, 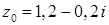 .
.
1.7. 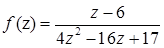 ,
, 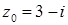 .
.
1.8. 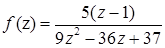 ,
, 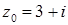 .
.
1.9. 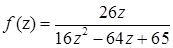 ,
, 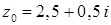 .
.
1.10. 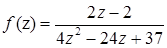 ,
, 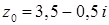 .
.
Задача 2. Найти все решения уравнения, используя формулу Муавра, ответ записать в тригонометрической форме.
2.1. 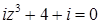 .
.
2.2 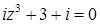 .
.
2.3. 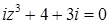 .
.
2.4. 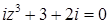 .
.
2.5. 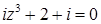 .
.
2.6. 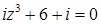 .
.
2.7. 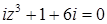 .
.
2.8. 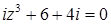 .
.
2.9. 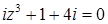 .
.
2.10. 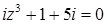 .
.
Задача 3. Решить матричное уравнение 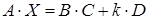
3.1. 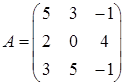 ,
, 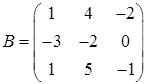 ,
, 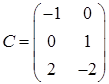 ,
, 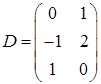 ,
, 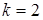 .
.
3.2. 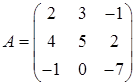 ,
, 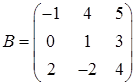 ,
, 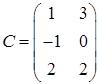 ,
, 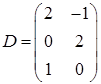 ,
, 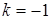
3.3. 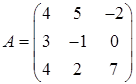 ,
, 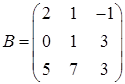 ,
, 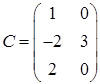 ,
, 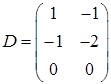 ,
, 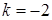
3.4. 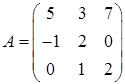 ,
, 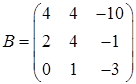 ,
, 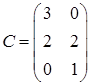 ,
, 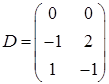 ,
, 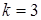
3.5. 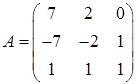 ,
, 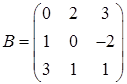 ,
, 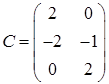 ,
, 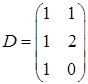 ,
, 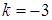
3.6. 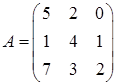 ,
, 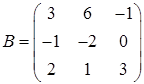 ,
, 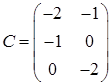 ,
, 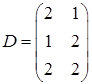 ,
, 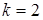
3.7. 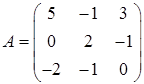 ,
, 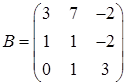 ,
, 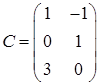 ,
, 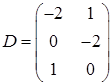 ,
, 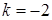
3.8. 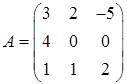 ,
, 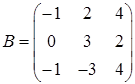 ,
, 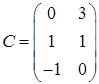 ,
, 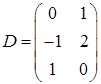 ,
, 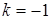
3.9. 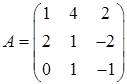 ,
, 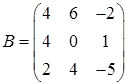 ,
, 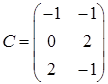 ,
, 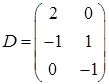 ,
, 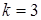
3.10. 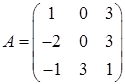 ,
, 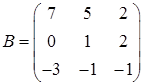 ,
, 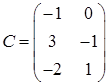 ,
, 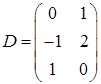 ,
, 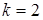
Задача 4. Решить систему уравнений, используя правило Крамера
4.1. 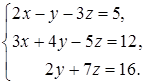 4.2.
4.2. 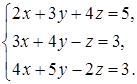
4.3. 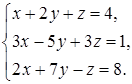 4.4.
4.4. 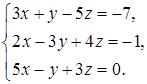
4.5. 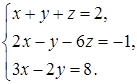 . 4.6.
. 4.6. 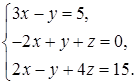
4.7. 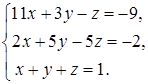 4.8.
4.8. 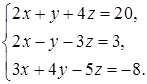
4.9. 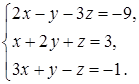 4.10.
4.10. 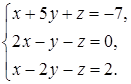
Задача 5. Доказать совместность системы и найти ее решение
5.1. 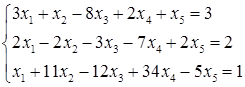
5.2. 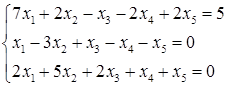
5.3. 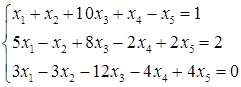
5.4. 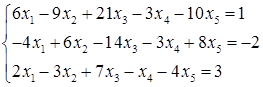
5.5. 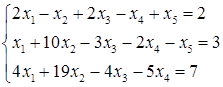
5.6. 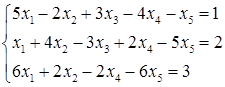
5.7. 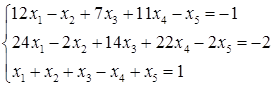
5.8. 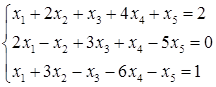
5.9. 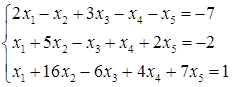
5.10. 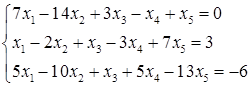
Контрольная работа № 2
Тема 3. Основные понятия векторной алгебры.
Тема 4. Аналитическая геометрия в пространстве.
Тема 5. Аналитическая геометрия на плоскости.
Задача 1. Найти косинус угла между векторами 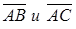 и площадь параллелограмма, построенного на этих векторах
и площадь параллелограмма, построенного на этих векторах
1.1. A(7, 0, 2), B(7, 1, 3), C(8, –14, 2).
1.2. A(2, 3, 2), B(–1, –3, –13), C(–3, –7, –3).
1.3. A(2, 2, 7), B(0, 0, 6), C(–2, 5, 7).
1.4. A(–1, 2, –3), B(0, 1, –2), C(–3, 4, –5).
1.5. A(0, 3, –6), B(9, 3, 6), C(12, 3, 3).
1.6. A(3, 3, –1), B(5, 1, –2), C(4, 1, –3).
1.7. A(–2, 1, 1), B(2, 3, –2), C(0, 0, 3).
1.8. A(1, 4, –1), B(–2, 4, –5), C(8, 4, 0).
1.9. A(0, 1 ,0), B(0, 2, 1), C(1, 2, 0).
1.10. A(–4, 0, 4), B(–1, 6, 7), C(1, 10, 9).
Задача 2. Даны координаты вершин пирамиды 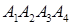 . Найти:
. Найти:
а) уравнение прямой 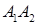 ;
;
б) уравнение плоскости 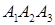 ;
;
в) уравнение высоты, опущенной из вершины 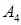 на грань
на грань 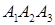 ;
;
г) вычислить объем пирамиды и расстояние от точки 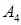 до плоскости
до плоскости 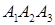 .
.
2.1. 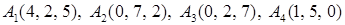
2.2. 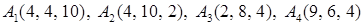
2.3. 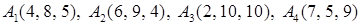
2.4. 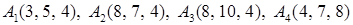
2.5. 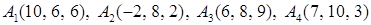
2.6. 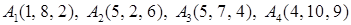
2.7. 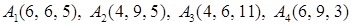
2.8. 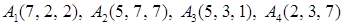
2.9. 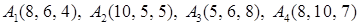
2.10. 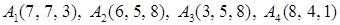
Задача 3. Даны координаты вершин треугольника 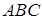 . Найти:
. Найти:
а) уравнение высоты 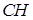 ;
;
б) уравнение медианы 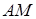 ;
;
в) точку 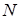 пересечения медианы
пересечения медианы 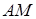 и высоты
и высоты 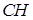 ;
;
г) уравнение прямой, проходящей через точку 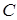 параллельно стороне
параллельно стороне 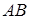 .
.
3.1. 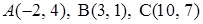 .
.
3.2. 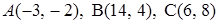 .
.
3.3. 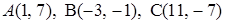 .
.
3.4. 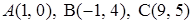 .
.
3.5. 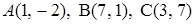 .
.
3.6. 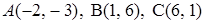 .
.
3.7. 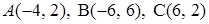 .
.
3.8. 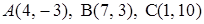 .
.
3.9. 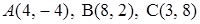 .
.
3.10. 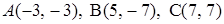 .
.
Задача 4. Составить уравнение линии, каждая точка 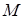 которой удовлетворяет заданным условиям:
которой удовлетворяет заданным условиям:
4.1. Отстоит от прямой 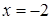 на расстоянии, в два раза большем, чем от точки
на расстоянии, в два раза большем, чем от точки 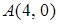 .
.
4.2. Отстоит от прямой 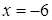 на расстоянии, в два раза большем, чем от точки
на расстоянии, в два раза большем, чем от точки 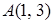 .
.
4.3. Отстоит от прямой 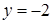 на расстоянии, в три раза большем, чем от точки
на расстоянии, в три раза большем, чем от точки 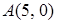 .
.
4.4. Отношение расстояний от точки 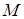 до точек в
до точек в 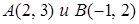 равно 0,75.
равно 0,75.
4.5. Сумма квадратов расстояний от точки 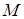 до точек
до точек 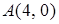
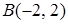 равна 28.
равна 28.
4.6. Отстоит от точки 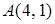 на расстоянии, в четыре два раза большем, чем от точки
на расстоянии, в четыре два раза большем, чем от точки 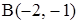 .
.
4.7. Отстоит от точки 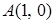 на расстоянии, в пять раз меньшем, чем от прямой
на расстоянии, в пять раз меньшем, чем от прямой 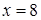 .
.
4.8. Отстоит от прямой 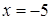 на расстоянии, в три раза большем, чем от точки
на расстоянии, в три раза большем, чем от точки 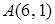 .
.
4.9. Отстоит от прямой 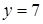 на расстоянии, в пять раз большем, чем от точки
на расстоянии, в пять раз большем, чем от точки 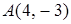 .
.
4.10. Отношение расстояний от точки 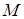 до точек в
до точек в 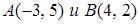 равно 1/3.
равно 1/3.
Контрольная работа № 3
Тема 6. Предел последовательности. Предел функции, непрерывность функции.
Задача 1. Вычислить пределы числовых последовательностей.
1.1. а) 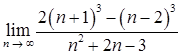 ,;
,;
б) 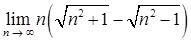 ;
;
в) 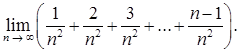
1.2. а) 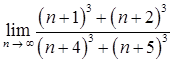 ;
;
б) 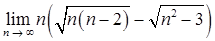 ;
;
в) 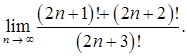
1.3. а) 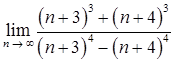 ;
;
б) 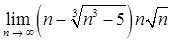 ;
;
в) 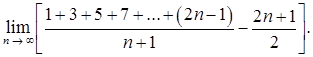
1.4. а) 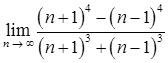 ;
;
б) 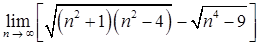 ;
;
в) 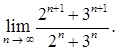
1.5. а) 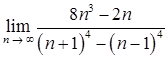 ;
;
б) 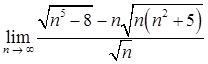 ;
;
в) 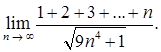
1.6. а) 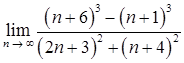 ;
;
б) 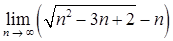 ;
;
в) 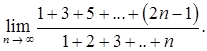
1.7. а) 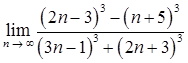 ;
;
б) 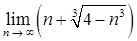 ;
;
в) 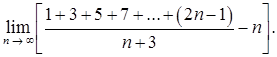
1.8. а) 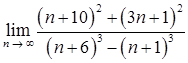 ;
;
б) 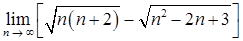 ;
;
в) 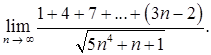
1.9. а) 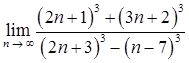 ;
;
б) 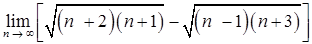 ;
;
в) 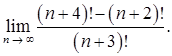
1.10. а) 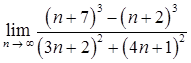 ;
;
б) 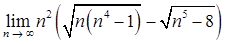 ;
;
в) 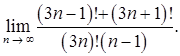
Задача 2. Вычислить пределы функций
2.1. а) 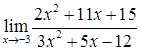 ; б)
; б) 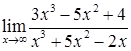 ;
;
в) 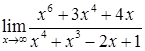 ; г)
; г) 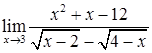 ;
;
д) 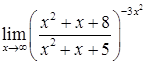 ; е
; е 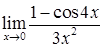 .
.
2.2. а) 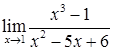 ; б)
; б) 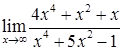 ;
;
в) 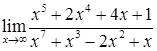 ; г)
; г) 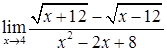 ;
;
д) 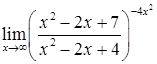 ; е)
; е) 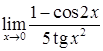
2.3. а) 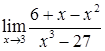 ; б)
; б) 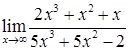 ;
;
в) 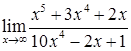 ; г)
; г) 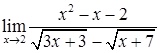 ;
;
д) 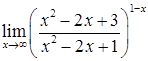 ; е)
; е) 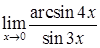 .
.
2.4. а) 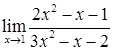 ; б)
; б) 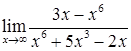 ;
;
в) 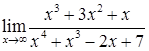 ; г)
; г) 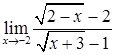 ;
;
д) 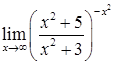 ; е)
; е) 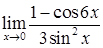 .
.
2.5. а) 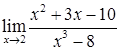 ; б)
; б) 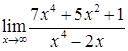 ;
;
в) 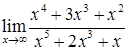 ; г)
; г) 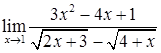 ;
;
д) 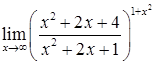 ; е)
; е) 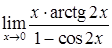 .
.
2.6. а) 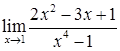 ; б)
; б) 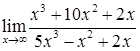 ;
;
в) 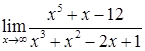 ; г)
; г) 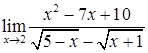 ;
;
д) 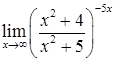 ; е)
; е) 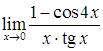 .
.
2.7. а) 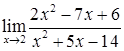 ; б)
; б) 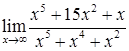 ;
;
в) 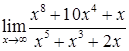 ; г)
; г) 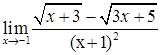 ;
;
д) 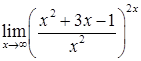 ; е)
; е) 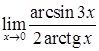 .
.
2.8. а) 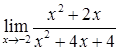 ; б)
; б) 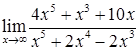 ;
;
в) 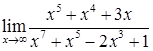 ; е)
; е) 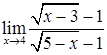 ;
;
д) 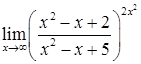 ; е)
; е) 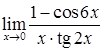 .
.
2.9. а) 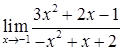 ; б)
; б) 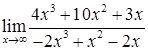 ;
;
в) 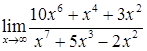 ; г)
; г) 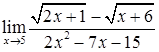 ;
;
д) 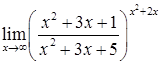 ; е)
; е) 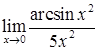 .
.
2.10. а) 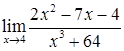 ; б)
; б) 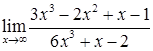 ;
;
в) 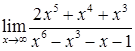 ; г)
; г) 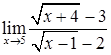 ;
;
д) 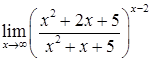 ; е)
; е) 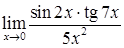 .
.
Задача 3. Исследовать данные функции на непрерывность и построить их графики
3.1. 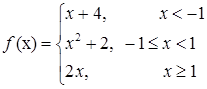
3.2. 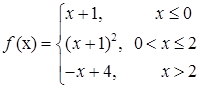
3.3. 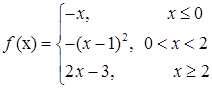
3.4. 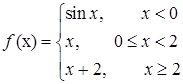
3.5. 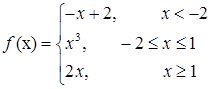
3.6. 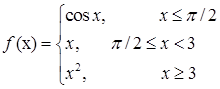
3.7. 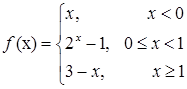
3.8. 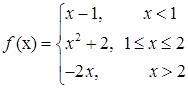
3.9. 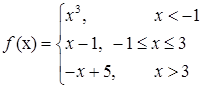
3.10. 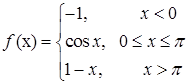
Дата: 2018-11-18, просмотров: 319.