ВЫСШАЯ МАТЕМАТИКА
Учебно-методическое пособие
По выполнению контрольных работ № 1, 2, 3
Институт машиностроения, энергетики и транспорта
Вологда
2018
Введение
Данное учебно-методическое пособие предназначено для студентов заочной и заочной ускоренной формы обучения по направлению подготовки электроэнергетика и электротехника, профиль: электроснабжение. Текст содержит варианты трех контрольных работ, которые необходимо самостоятельно выполнить студентам в первом семестре, разбор задач, аналогичных предложенным в контрольных работах. Кроме того, в пособии приведен справочный теоретический материал, необходимый для выполнения контрольных заданий. Номер варианта контрольной работы определяется в соответствии с последней цифрой шифра студента – номера его зачетной книжки. Каждая работа выполняется в отдельной тетради, задачи должны быть представлены в том порядке, в котором они указаны в контрольной работе. Компьютерное оформление работ на проверку не принимается.
Задачи для контрольных заданий
Контрольная работа № 1
Тема 1. Комплексные числа.
Тема 2. Основные понятия линейной алгебры.
Задача 1. Найти: а) область определения функции 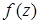 ;
;
б) значение функции 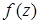 в точке
в точке 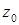 .
.
1.1. 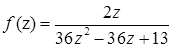 ,
, 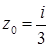 .
.
1.2. 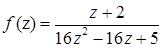 ,
,  .
.
1.3. 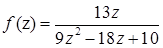 ,
, 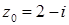 .
.
1.4.  ,
, 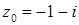 .
.
1.5.  ,
, 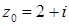 .
.
1.6. 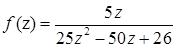 ,
, 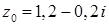 .
.
1.7. 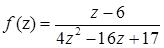 ,
, 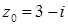 .
.
1.8. 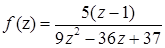 ,
, 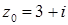 .
.
1.9.  ,
, 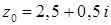 .
.
1.10. 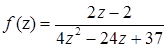 ,
,  .
.
Задача 2. Найти все решения уравнения, используя формулу Муавра, ответ записать в тригонометрической форме.
2.1.  .
.
2.2 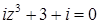 .
.
2.3.  .
.
2.4. 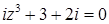 .
.
2.5. 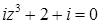 .
.
2.6. 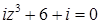 .
.
2.7. 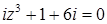 .
.
2.8. 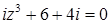 .
.
2.9. 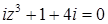 .
.
2.10. 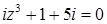 .
.
Задача 3. Решить матричное уравнение 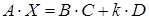
3.1. 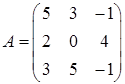 ,
,  ,
, 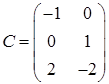 ,
,  ,
, 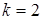 .
.
3.2. 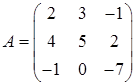 ,
,  ,
,  ,
, 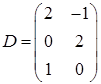 ,
, 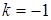
3.3.  ,
, 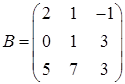 ,
,  ,
, 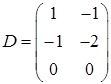 ,
, 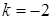
3.4. 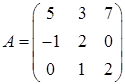 ,
,  ,
, 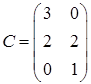 ,
, 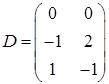 ,
, 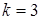
3.5.  ,
, 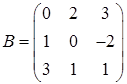 ,
, 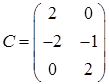 ,
,  ,
, 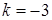
3.6. 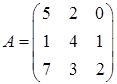 ,
, 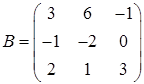 ,
, 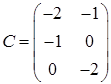 ,
, 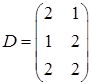 ,
, 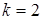
3.7. 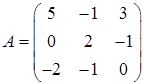 ,
,  ,
, 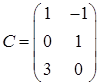 ,
, 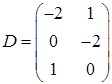 ,
, 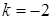
3.8. 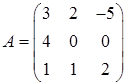 ,
, 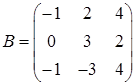 ,
, 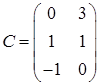 ,
,  ,
, 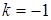
3.9. 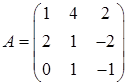 ,
, 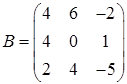 ,
, 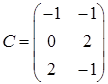 ,
, 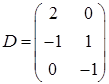 ,
, 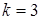
3.10. 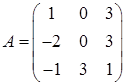 ,
, 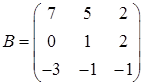 ,
, 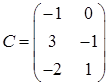 ,
,  ,
, 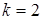
Задача 4. Решить систему уравнений, используя правило Крамера
4.1. 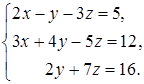 4.2.
4.2. 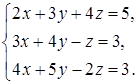
4.3. 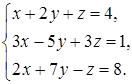 4.4.
4.4. 
4.5. 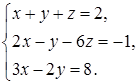 . 4.6.
. 4.6. 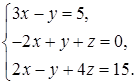
4.7. 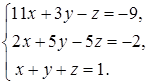 4.8.
4.8. 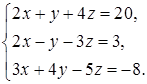
4.9. 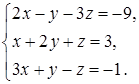 4.10.
4.10. 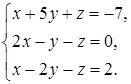
Задача 5. Доказать совместность системы и найти ее решение
5.1. 
5.2. 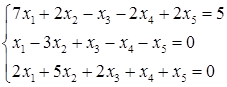
5.3. 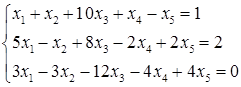
5.4. 
5.5. 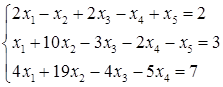
5.6. 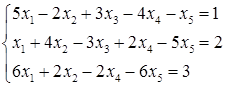
5.7. 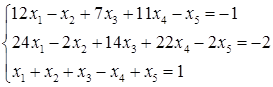
5.8. 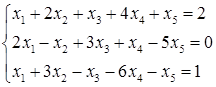
5.9. 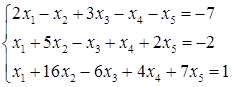
5.10. 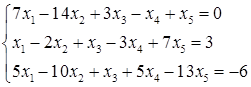
Контрольная работа № 2
Тема 3. Основные понятия векторной алгебры.
Тема 4. Аналитическая геометрия в пространстве.
Тема 5. Аналитическая геометрия на плоскости.
Задача 1. Найти косинус угла между векторами 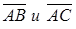 и площадь параллелограмма, построенного на этих векторах
и площадь параллелограмма, построенного на этих векторах
1.1. A(7, 0, 2), B(7, 1, 3), C(8, –14, 2).
1.2. A(2, 3, 2), B(–1, –3, –13), C(–3, –7, –3).
1.3. A(2, 2, 7), B(0, 0, 6), C(–2, 5, 7).
1.4. A(–1, 2, –3), B(0, 1, –2), C(–3, 4, –5).
1.5. A(0, 3, –6), B(9, 3, 6), C(12, 3, 3).
1.6. A(3, 3, –1), B(5, 1, –2), C(4, 1, –3).
1.7. A(–2, 1, 1), B(2, 3, –2), C(0, 0, 3).
1.8. A(1, 4, –1), B(–2, 4, –5), C(8, 4, 0).
1.9. A(0, 1 ,0), B(0, 2, 1), C(1, 2, 0).
1.10. A(–4, 0, 4), B(–1, 6, 7), C(1, 10, 9).
Задача 2. Даны координаты вершин пирамиды 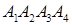 . Найти:
. Найти:
а) уравнение прямой 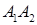 ;
;
б) уравнение плоскости 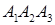 ;
;
в) уравнение высоты, опущенной из вершины  на грань
на грань 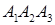 ;
;
г) вычислить объем пирамиды и расстояние от точки  до плоскости
до плоскости 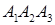 .
.
2.1. 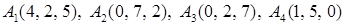
2.2. 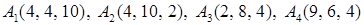
2.3. 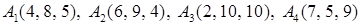
2.4. 
2.5. 
2.6. 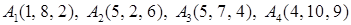
2.7. 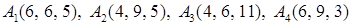
2.8. 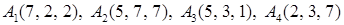
2.9. 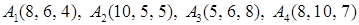
2.10. 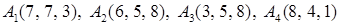
Задача 3. Даны координаты вершин треугольника 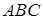 . Найти:
. Найти:
а) уравнение высоты 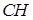 ;
;
б) уравнение медианы 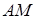 ;
;
в) точку  пересечения медианы
пересечения медианы 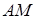 и высоты
и высоты 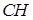 ;
;
г) уравнение прямой, проходящей через точку  параллельно стороне
параллельно стороне 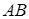 .
.
3.1.  .
.
3.2. 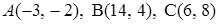 .
.
3.3.  .
.
3.4. 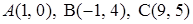 .
.
3.5. 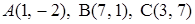 .
.
3.6. 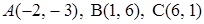 .
.
3.7. 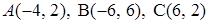 .
.
3.8.  .
.
3.9. 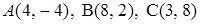 .
.
3.10. 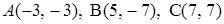 .
.
Задача 4. Составить уравнение линии, каждая точка 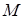 которой удовлетворяет заданным условиям:
которой удовлетворяет заданным условиям:
4.1. Отстоит от прямой 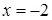 на расстоянии, в два раза большем, чем от точки
на расстоянии, в два раза большем, чем от точки 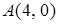 .
.
4.2. Отстоит от прямой 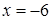 на расстоянии, в два раза большем, чем от точки
на расстоянии, в два раза большем, чем от точки  .
.
4.3. Отстоит от прямой 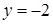 на расстоянии, в три раза большем, чем от точки
на расстоянии, в три раза большем, чем от точки 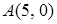 .
.
4.4. Отношение расстояний от точки 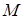 до точек в
до точек в 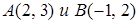 равно 0,75.
равно 0,75.
4.5. Сумма квадратов расстояний от точки 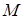 до точек
до точек 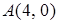
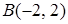 равна 28.
равна 28.
4.6. Отстоит от точки 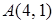 на расстоянии, в четыре два раза большем, чем от точки
на расстоянии, в четыре два раза большем, чем от точки  .
.
4.7. Отстоит от точки  на расстоянии, в пять раз меньшем, чем от прямой
на расстоянии, в пять раз меньшем, чем от прямой 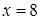 .
.
4.8. Отстоит от прямой  на расстоянии, в три раза большем, чем от точки
на расстоянии, в три раза большем, чем от точки 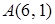 .
.
4.9. Отстоит от прямой  на расстоянии, в пять раз большем, чем от точки
на расстоянии, в пять раз большем, чем от точки 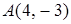 .
.
4.10. Отношение расстояний от точки 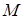 до точек в
до точек в 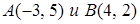 равно 1/3.
равно 1/3.
Контрольная работа № 3
Тема 6. Предел последовательности. Предел функции, непрерывность функции.
Задача 1. Вычислить пределы числовых последовательностей.
1.1. а) 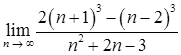 ,;
,;
б) 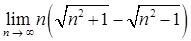 ;
;
в) 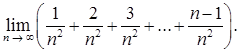
1.2. а) 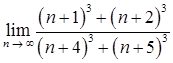 ;
;
б) 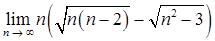 ;
;
в) 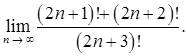
1.3. а) 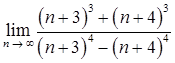 ;
;
б)  ;
;
в) 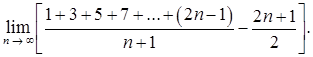
1.4. а) 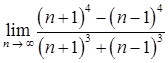 ;
;
б) 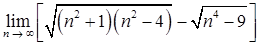 ;
;
в) 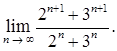
1.5. а) 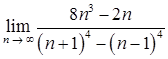 ;
;
б)  ;
;
в) 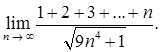
1.6. а)  ;
;
б) 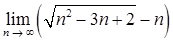 ;
;
в) 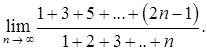
1.7. а) 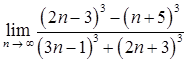 ;
;
б) 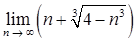 ;
;
в) 
1.8. а) 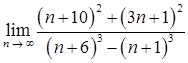 ;
;
б) 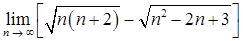 ;
;
в) 
1.9. а) 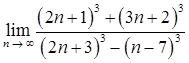 ;
;
б) 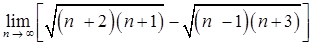 ;
;
в) 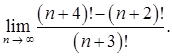
1.10. а) 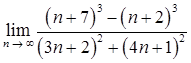 ;
;
б) 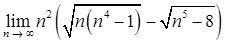 ;
;
в) 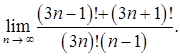
Задача 2. Вычислить пределы функций
2.1. а) 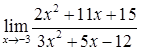 ; б)
; б) 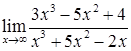 ;
;
в) 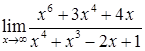 ; г)
; г) 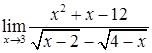 ;
;
д) 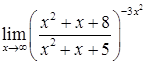 ; е
; е 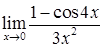 .
.
2.2. а)  ; б)
; б) 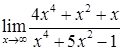 ;
;
в) 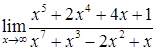 ; г)
; г) 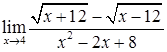 ;
;
д) 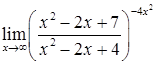 ; е)
; е) 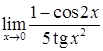
2.3. а) 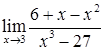 ; б)
; б) 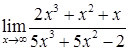 ;
;
в) 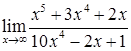 ; г)
; г) 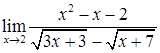 ;
;
д)  ; е)
; е)  .
.
2.4. а) 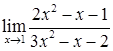 ; б)
; б) 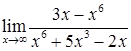 ;
;
в) 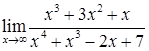 ; г)
; г)  ;
;
д) 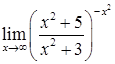 ; е)
; е) 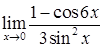 .
.
2.5. а) 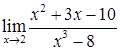 ; б)
; б) 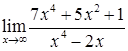 ;
;
в) 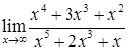 ; г)
; г) 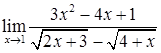 ;
;
д) 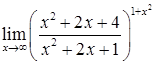 ; е)
; е) 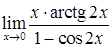 .
.
2.6. а) 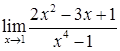 ; б)
; б) 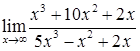 ;
;
в) 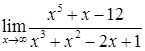 ; г)
; г) 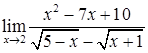 ;
;
д) 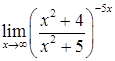 ; е)
; е) 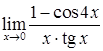 .
.
2.7. а) 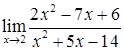 ; б)
; б)  ;
;
в) 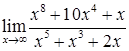 ; г)
; г) 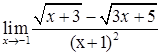 ;
;
д) 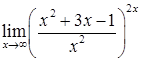 ; е)
; е)  .
.
2.8. а) 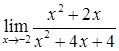 ; б)
; б) 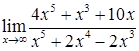 ;
;
в) 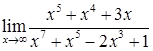 ; е)
; е) 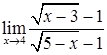 ;
;
д) 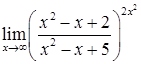 ; е)
; е)  .
.
2.9. а) 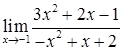 ; б)
; б) 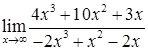 ;
;
в)  ; г)
; г)  ;
;
д) 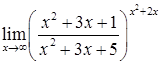 ; е)
; е) 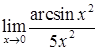 .
.
2.10. а) 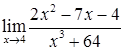 ; б)
; б) 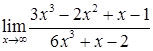 ;
;
в) 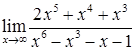 ; г)
; г) 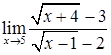 ;
;
д) 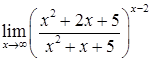 ; е)
; е) 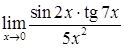 .
.
Задача 3. Исследовать данные функции на непрерывность и построить их графики
3.1. 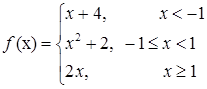
3.2. 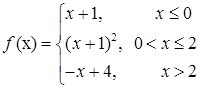
3.3. 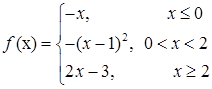
3.4. 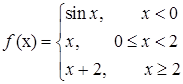
3.5. 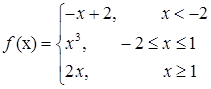
3.6. 
3.7. 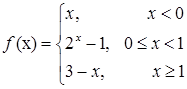
3.8. 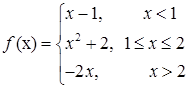
3.9. 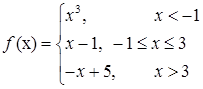
3.10. 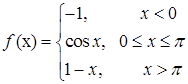
Решение.
а) Так как 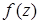 является дробно-рациональной функцией, то областью определения этой функции представляет собой множество всех комплексных чисел, исключая те, которые обращают знаменатель в ноль. Составим и решим уравнение
является дробно-рациональной функцией, то областью определения этой функции представляет собой множество всех комплексных чисел, исключая те, которые обращают знаменатель в ноль. Составим и решим уравнение  . Уравнение имеет комплексные корни, так как его дискриминант
. Уравнение имеет комплексные корни, так как его дискриминант 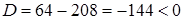 . Найдем корни:
. Найдем корни:  . Таким образом, областью определения функции
. Таким образом, областью определения функции 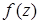 является множество всех комплексных чисел кроме
является множество всех комплексных чисел кроме 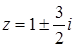 .
.
б) Найдем значение функции в заданной точке  .
.
Выполним действия
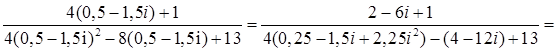
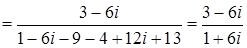 .
.
Для того, чтобы поделить два комплексных числа числитель и знаменатель дроби умножим на число сопряженной знаменателю получим 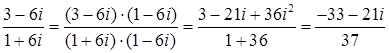 .
.
Таким образом, 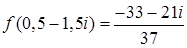 .
.
Задача 2. Найти все решения уравнения  , используя формулу Муавра, ответ записать в тригонометрической форме.
, используя формулу Муавра, ответ записать в тригонометрической форме.
Решение.
Преобразуем уравнение так, чтобы выразить 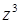 .
.
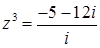 или
или 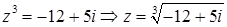 .
.
Найдем тригонометрическую форму комплексного числа:
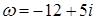 .
. 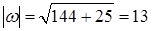 ,
,
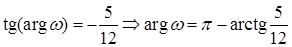 так как
так как  .
.
Тогда 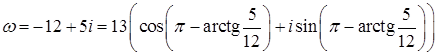 .
.
Используем формулу Муавра
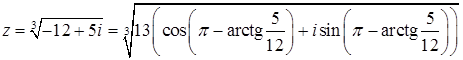
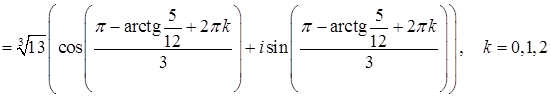 .
.
Уравнение 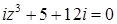 имеет 3 комплексных корня, получаемых при различных значениях
имеет 3 комплексных корня, получаемых при различных значениях 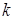 .
.

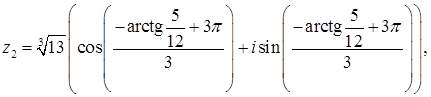
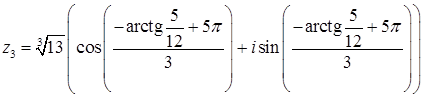 .
.
Задача 3. Решить матричное уравнение 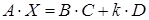 , где
, где
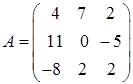 ,
, 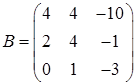 ,
, 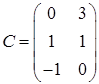 ,
, 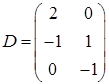 ,
, 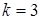
Решение:
Убедимся, что  матрица не является вырожденной, то есть обладает обратной матрицей. Для этого вычислим её определитель:
матрица не является вырожденной, то есть обладает обратной матрицей. Для этого вычислим её определитель:
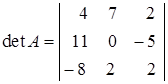 .
.
Разложим определитель, например, по элементам второго столбца:

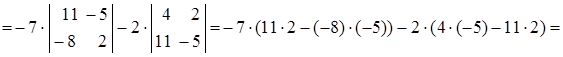 210.
210.
Определитель отличен от нуля, поэтому обратная матрица существует, и мы можем вычислить обратную матрицу по формуле:
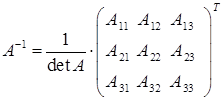 .
.
Вычислим алгебраические дополнения:
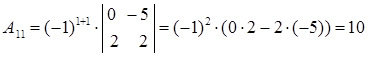
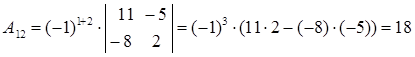
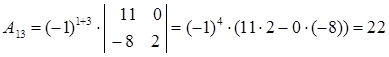
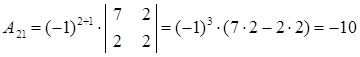
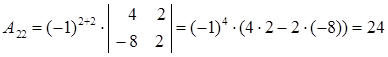


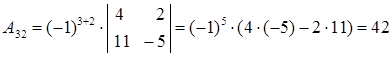

Таким образом, матрица, составленная из алгебраических дополнений, имеет вид:
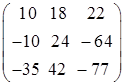 (
( 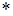 )
)
Транспонирование матрицы – такое преобразование этой матрицы, при котором ее строки становятся столбцами с теми же номерами. Транспонированная матрица к матрице ( 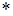 ) будет выглядеть так:
) будет выглядеть так:
 ,
,
тогда
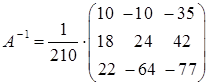 или
или  .
.
Таким образом, уравнение имеет единственное решение. Выполним преобразование левой части уравнения
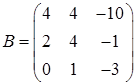 ,
,  ,
, 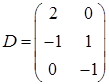 ,
, 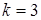
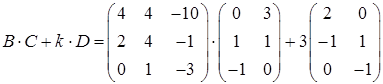 .
.
Обозначим произведение матриц 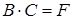 , где
, где  матрица размерности
матрица размерности 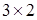 элементами
элементами  .
.
Получим 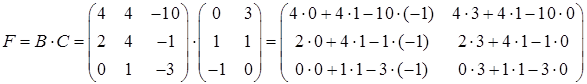 .
. 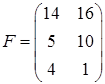 .
.
Матрица 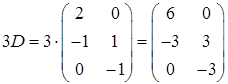
и  .
.
Исходное уравнение принимает вид
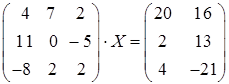 .
.
Умножим левую и правую части уравнения слева на 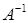 , получаем
, получаем 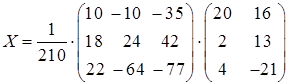 ,
,
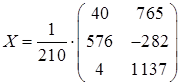 .
.
Задача 4. Решить систему уравнений, используя правило Крамера
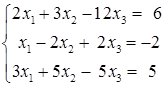
Решение:
Вычислим определитель матрицы, составленной из коэффициентов, стоящих при переменных в предложенной системе линейных уравнений:

Его назовем главным определителем, 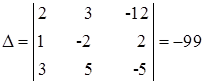 . Если главный определитель отличен от нуля, то система имеет единственное решение и найти его можно по правилу Крамера. Для этого заменим в матрице коэффициентов первый столбец на столбец свободных членов, и вычислим определитель такой матрицы:
. Если главный определитель отличен от нуля, то система имеет единственное решение и найти его можно по правилу Крамера. Для этого заменим в матрице коэффициентов первый столбец на столбец свободных членов, и вычислим определитель такой матрицы:
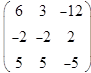
| 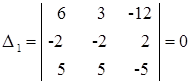
|
Аналогичным образом, получаем матрицы с замененными вторым и третьим столбцами соответственно, затем, вычислим определители этих матриц.

| 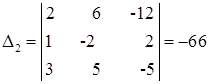
|
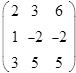
| 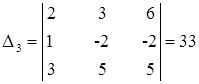
|
Решение системы можно найти таким образом:
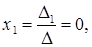
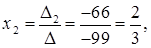
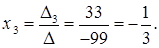
Задача 5. Доказать совместность системы и найти ее решение

Решение:
Запишем расширенную матрицу системы
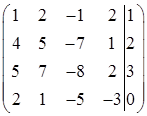
Вычтем из второй строки первую, предварительно умноженную на 4
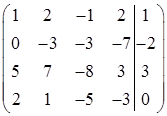
Вычтем из третьей строки первую, умноженную на 5
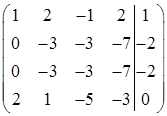
Наконец, вычтем из четвертой строки первую, умноженную на два
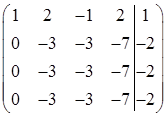
Затем вторую строку умножим на – 1 и прибавим ее к третьей и четвертой строкам
 .
.
Ранг матрицы равен рангу расширенной матрицы и равен 2. Число свободных неизвестных в общем случае равно 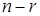 , где n – количество неизвестных системы, r – ранг матрицы системы. У нас число свободных неизвестных равно 4 – 2 = 2.
, где n – количество неизвестных системы, r – ранг матрицы системы. У нас число свободных неизвестных равно 4 – 2 = 2.
Новой расширенной матрице соответствует система
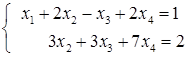 .
.
Пусть 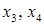 – свободные переменные, принимающие любые действительные значения. Все остальные неизвестные выразим через них. Из второго уравнения системы выразим
– свободные переменные, принимающие любые действительные значения. Все остальные неизвестные выразим через них. Из второго уравнения системы выразим 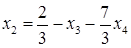 .
.
Подставляя найденное выражение для  в первое уравнение, получаем
в первое уравнение, получаем 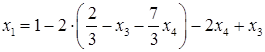
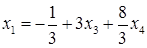 .
.
Таким образом, общее решение системы имеет вид 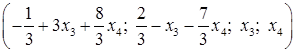 (
( 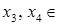 R).
R).
Решение.
а) Найдем координаты вектора 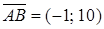 . Т.к. высота
. Т.к. высота  , то
, то 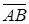 является нормальным вектором для прямой
является нормальным вектором для прямой 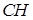 , таким образом уравнение высоты имеет вид
, таким образом уравнение высоты имеет вид 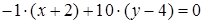 .
.
Упростим полученное уравнение и получим 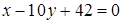 .
.
б) Вычислим координаты точки 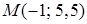 , как координаты середины отрезка
, как координаты середины отрезка 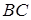 . Тогда уравнение прямой, проходящей через две заданные точки имеет вид
. Тогда уравнение прямой, проходящей через две заданные точки имеет вид 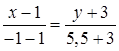 .
.
Выполним преобразование полученного уравнения
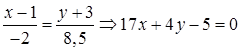 .
.
в) Вектор 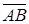 коллинеарен искомой прямой, а значит служит для этой прямой направляющим вектором. Каноническое уравнение этой прямой имеет вид
коллинеарен искомой прямой, а значит служит для этой прямой направляющим вектором. Каноническое уравнение этой прямой имеет вид 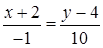 . Выполнив преобразования, получим
. Выполнив преобразования, получим 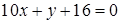 .
.
Задача 4. Составить уравнение линии, каждая точка  которой отстоит от точки
которой отстоит от точки 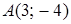 на расстоянии в три раза большем, чем от прямой
на расстоянии в три раза большем, чем от прямой 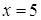 .
.
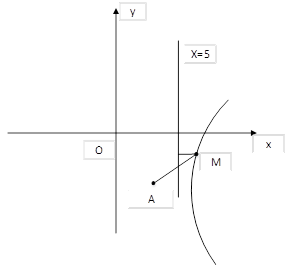 рис.1
рис.1
Решение. Пусть точка 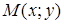 принадлежит искомой линии. Тогда расстояние
принадлежит искомой линии. Тогда расстояние  в три раза больше, чем расстояние
в три раза больше, чем расстояние 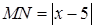 . Составим уравнение
. Составим уравнение 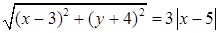 и преобразуем его.
и преобразуем его. 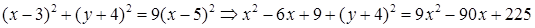
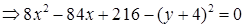 . Продолжим преобразования
. Продолжим преобразования 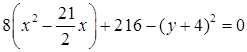 . Выделим полный квадрат по переменной
. Выделим полный квадрат по переменной 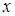 и получим
и получим  или
или 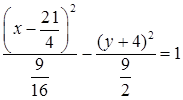 . Получили уравнение гиперболы, центр которой находится в точке с
. Получили уравнение гиперболы, центр которой находится в точке с  , а полуоси
, а полуоси 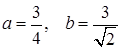 .
.
 рис.2
рис.2
Задача 2.
1) Вычислить предел функции 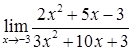 .
.
Решение. Используя основные теоремы о пределах видим, что  и
и  . Таким образом выражение
. Таким образом выражение 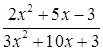 представляет неопределенность
представляет неопределенность 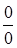 при
при  . Чтобы раскрыть эту неопределенность числитель и знаменатель дроби разложим на множители, найдя корни многочленов. Уравнение
. Чтобы раскрыть эту неопределенность числитель и знаменатель дроби разложим на множители, найдя корни многочленов. Уравнение 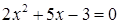 имеет корни
имеет корни 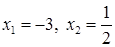 . Уравнение
. Уравнение 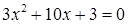 имеет корни
имеет корни  . Тогда
. Тогда  .
.
2) Вычислить предел функции 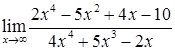 .
.
Решение. Так как числитель и знаменатель дроби неограниченно возрастают при неограниченном возрастании аргумента, то выражение  представляет неопределенность
представляет неопределенность  . раскроем эту неопределенность поделив числитель и знаменатель дроби на старшую степень переменного т.е. на
. раскроем эту неопределенность поделив числитель и знаменатель дроби на старшую степень переменного т.е. на 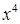 . Получим
. Получим 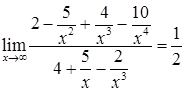 .
.
3) Вычислить предел функции 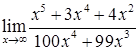 .
.
Решение. Также как в предыдущем случае, неопределенность  и раскрываем ее аналогично.
и раскрываем ее аналогично. 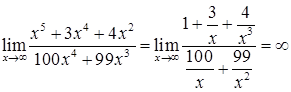 .
.
4) Вычислить предел функции 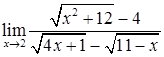 .
.
Решение. Выражение 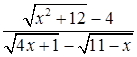 представляет неопределенность
представляет неопределенность 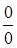 при
при 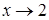 .для того, чтобы раскрыть эту неопределенность преобразуем дробь умножив сначала числитель и знаменатель на выражение сопряженное числителю
.для того, чтобы раскрыть эту неопределенность преобразуем дробь умножив сначала числитель и знаменатель на выражение сопряженное числителю
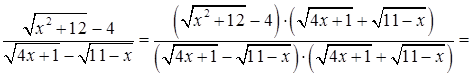
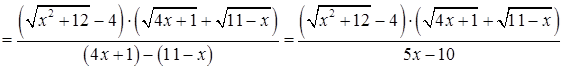 . Затем аналогично умножим числитель и знаменатель дроби на выражение сопряженное числителю исходной дроби
. Затем аналогично умножим числитель и знаменатель дроби на выражение сопряженное числителю исходной дроби 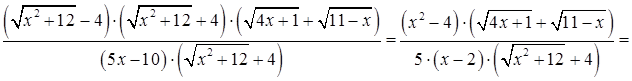
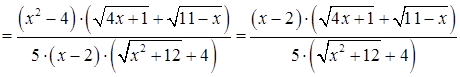 . Выполнив преобразования, вычислим предел, используя основные теоремы о пределах
. Выполнив преобразования, вычислим предел, используя основные теоремы о пределах 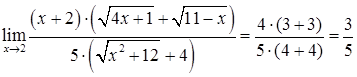 .
.
5) Вычислить предел функции 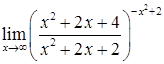 .
.
Решение. Убедимся, что выражение  представляет неопределенность вида
представляет неопределенность вида  . Действительно
. Действительно 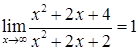 , а
, а  . Преобразуем основание степени
. Преобразуем основание степени  , тогда вся степень может быть преобразована следующим образом
, тогда вся степень может быть преобразована следующим образом 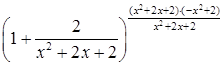 . Продолжим вычисление предела, используя свойство непрерывности функции
. Продолжим вычисление предела, используя свойство непрерывности функции 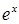 .
.  .
.
5) Вычислить предел функции 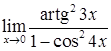 .
.
Решение. Воспользуемся таблицей эквивалентных бесконечно малых величин 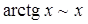 ,
, 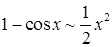 при
при  . Тогда
. Тогда 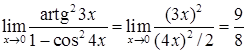 .
.
Задача 3. Исследовать данную функцию на непрерывность и построить ее график  .
.
Решение. На интервалах  функция непрерывна, поэтому исследовать ее на непрерывность нужно в точках
функция непрерывна, поэтому исследовать ее на непрерывность нужно в точках 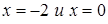 . Вычислим значения функции и ее односторонние пределы в данных точках.
. Вычислим значения функции и ее односторонние пределы в данных точках.
а) В точке 
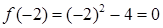 ,
,  ,
,  . Односторонние пределы равны между собой и равны значению функции в данной точке, значит функция в точке
. Односторонние пределы равны между собой и равны значению функции в данной точке, значит функция в точке 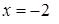 непрерывна.
непрерывна.
б) В точке 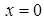
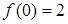 ,
,  ,
,  . Односторонние пределы конечны, но не равны между собой, значит, функция в точке
. Односторонние пределы конечны, но не равны между собой, значит, функция в точке 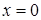 имеет конечный разрыв (разрыв первого рода).
имеет конечный разрыв (разрыв первого рода).
Комплексные числа.
На множестве действительных чисел невозможно решить уравнение  . Введем условный символ
. Введем условный символ 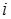 , который называется «мнимая единица», основное свойство которой
, который называется «мнимая единица», основное свойство которой 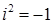 , или
, или 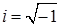 .
.
Тогда числа вида 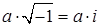 назовем мнимыми числами, а числа вида
назовем мнимыми числами, а числа вида 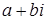 – комплексными.
– комплексными.
Комплексные числа изображают точкой на координатной плоскости.
Два комплексных числа 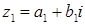
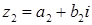 равны, если равны их действительные и мнимые части:
равны, если равны их действительные и мнимые части: 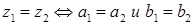 . Нулем называют число
. Нулем называют число  , а единицей
, а единицей 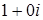 .
.
Комплексные числа можно складывать по правилу:
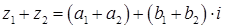 .
.
Умножают комплексные числа по правилу:
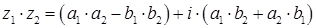
Существует обратный элемент  , имеющий вид
, имеющий вид  .
.
Обозначим: 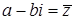 – число сопряженное с z .
– число сопряженное с z .
Тогда правило деления таково: 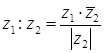 .
.
Тригонометрическая форма комплексного числа 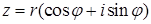 ,
,
Где 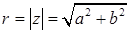 – модуль комплексного числа, угол
– модуль комплексного числа, угол 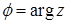 – его аргумент. В тригонометрической форме комплексные числа можно умножать, возводить в натуральную степень и извлекать корень из комплексного числа по формулам:
– его аргумент. В тригонометрической форме комплексные числа можно умножать, возводить в натуральную степень и извлекать корень из комплексного числа по формулам:
Если  , тогда
, тогда
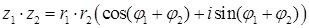 ;
;
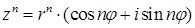 - формула Муавра;
- формула Муавра;
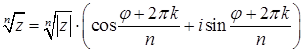 , где
, где 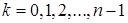 к = 0,1,2,…,n-1 – формула Муавра.
к = 0,1,2,…,n-1 – формула Муавра.
На множестве комплексных чисел квадратное уравнение 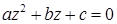 имеет всегда два корня
имеет всегда два корня 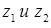 . А любое уравнение
. А любое уравнение 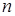 -ой степени
-ой степени 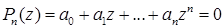 имеет
имеет 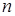 корней действительных или комплексных.
корней действительных или комплексных.
Матрицы, определители и их свойства.
Прямоугольной матрицей размерности 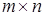 называется таблица, состоящая из m строк и n столбцов.
называется таблица, состоящая из m строк и n столбцов.
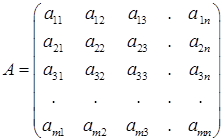 =
= 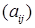 (
( 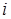 – номер строки,
– номер строки, 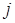 – номер столбца)
– номер столбца)
Если 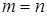 , то матрица называется квадратной порядка n.
, то матрица называется квадратной порядка n.
При 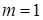 – матрица строка; при
– матрица строка; при 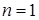 – матрица столбец.
– матрица столбец.
Две матрицы называются равными, если имеют одинаковую размерность и равны элементы, стоящие на одинаковых местах. 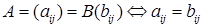
Суммой двух матриц одинаковой размерности называется матрица, составленная из сумм соответствующих элементов матриц 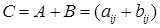 . Существует нулевая матрица
. Существует нулевая матрица 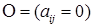 .
.
Произведением матрицы  на число
на число 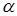 называется матрица
называется матрица 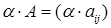 .
.
Произведением матриц 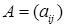 размерности
размерности 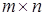 и
и 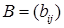 размерности
размерности 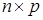 называется матрица
называется матрица  , коэффициенты которой вычисляются по правилу:
, коэффициенты которой вычисляются по правилу: 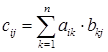 . Элемент, стоящий на пересечении
. Элемент, стоящий на пересечении 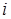 -ой строки и
-ой строки и 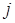 -того столбца равен сумме произведений элементов
-того столбца равен сумме произведений элементов 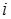 -ой строки матрицы
-ой строки матрицы  на соответствующие элементы
на соответствующие элементы  -того столбца матрицы В.
-того столбца матрицы В.
Произведение матриц не коммутативно, т.е. 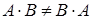 .
.
Существует  – единичная матрица
– единичная матрица 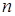 - го порядка
- го порядка
Для матрицы 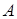 размерности
размерности 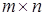 выполняются свойства
выполняются свойства
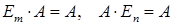 . Если
. Если  и
и 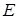 квадратные матрицы одного порядка, то
квадратные матрицы одного порядка, то 
Если для данной матрицы 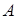 существует матрица
существует матрица 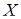 :
: 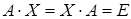 , то X называется обратной A и обозначается
, то X называется обратной A и обозначается 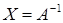 .
.
Каждой квадратной матрице 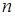 -го порядка можно сопоставить число, которое называется определителем матрицы и вычисляется по определенному правилу.
-го порядка можно сопоставить число, которое называется определителем матрицы и вычисляется по определенному правилу.
Определителем второго порядка называется таблица  , значение которого находится по правилу
, значение которого находится по правилу  .
.
Определитель третьего порядка вычисляется следующим образом: 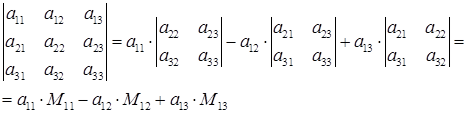
Здесь 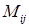 – минор элемента
– минор элемента 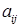 т.е. определитель второго порядка, полученный из данного вычеркиванием
т.е. определитель второго порядка, полученный из данного вычеркиванием 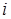 - ой строки и
- ой строки и 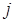 - того столбца, на пересечении которых стоит данный элемент.
- того столбца, на пересечении которых стоит данный элемент.
Определитель 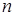 - го порядка вычисляется так:
- го порядка вычисляется так:
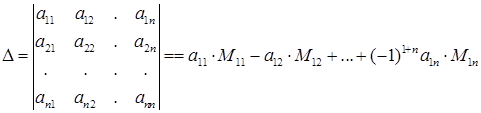 ,
,
где 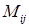 - минор элемента
- минор элемента 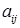 т.е. определитель
т.е. определитель 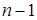 - го порядка, полученный вычеркиванием
- го порядка, полученный вычеркиванием  - ой строки и
- ой строки и  - того столбца, на пересечении которых стоит данный элемент. Алгебраическим дополнением элемента
- того столбца, на пересечении которых стоит данный элемент. Алгебраическим дополнением элемента 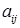 назовем минор со знаком, выбранным по правилу:
назовем минор со знаком, выбранным по правилу: 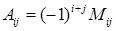 .
.
Тогда  . Говорят, что определитель вычислен разложением по элементам первой строки.
. Говорят, что определитель вычислен разложением по элементам первой строки.
Перечислим некоторые свойства определителей.
1) При транспонировании матриц определители не меняются.
Под транспонированием матриц понимают преобразование матрицы (и определителя) при котором строки и столбцы меняются местами.
Следствия: а) одинаковые свойства для строк и столбцов.
б) 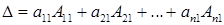 – разложение по элементам первого столбца.
– разложение по элементам первого столбца.
2) Если в квадратной матрице какие-нибудь две строки (или столбца) поменять местами, то определитель поменяет знак.
3) Определитель может быть разложен по элементам любой строки или столбца.
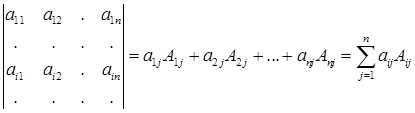
разложение по элементам 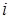 – ой строки.
– ой строки.
Следствия: а) если одна из строк (столбцов) состоит из нулей, то
определитель равен нулю.
б) если элементы строки (столбца) умножить на одно и тоже
число, то определитель умножится на это число.
4) Если определитель имеет две одинаковые строки (столбца), то он равен нулю.
5) Если матрица имеет две пропорциональные строки (столбца), то он равен нулю.
6) Определитель не изменится, если к элементам одной строки прибавить соответствующие элементы другой строки, умноженные на одно и тоже постоянное число.
Вернемся к задаче вычисления матрицы обратной данной. Сформулируем правило: всякая невырожденная матрица 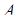 (определитель
(определитель 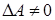 ) имеет обратную матрицу, которая вычисляется по формуле
) имеет обратную матрицу, которая вычисляется по формуле 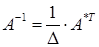 , где
, где
матрица  составленная из алгебраических дополнений элементов данной матрицы.
составленная из алгебраических дополнений элементов данной матрицы.
Векторы и действия с ними.
Вектором назовем направленный отрезок в пространстве. Обозначения: 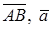 . Длина отрезка AB является длиной вектора
. Длина отрезка AB является длиной вектора 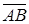 . Нулевой вектор – вектор имеющий нулевую длину.
. Нулевой вектор – вектор имеющий нулевую длину.
Векторы коллинеарны, если они лежат на одной прямой или на параллельных прямых. Векторы компланарны, если они лежат в одной плоскости, или в параллельных плоскостях.
Два вектора называются равными, если они
a) коллинеарны,
b) одинаково направлены,
c) имеют равные длины.
Из определения следует, что вектор можно переносить параллельно самому себе в любую точку пространства. Такой вектор называется свободным.
Пусть даны два вектора 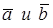 . Построим равные им векторы
. Построим равные им векторы 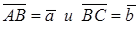 . Тогда вектор
. Тогда вектор 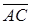 называется суммой векторов
называется суммой векторов 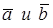 .
.  .
.
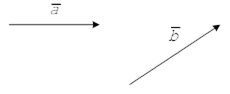
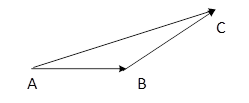
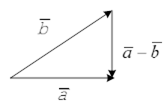
Этот способ называется «правило треугольника». Векторы можно складывать и по «правилу параллелограмма» (см рис.)

Разностью двух векторов 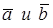 называется сумма векторов
называется сумма векторов 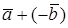 . Вычитание действие обратное сложению
. Вычитание действие обратное сложению 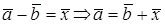
Произведение вектора  на число
на число 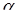 называется вектор
называется вектор 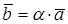 :
:
а) 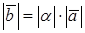
б)  коллинеарен
коллинеарен 
в) 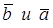 одинаково направлены, если
одинаково направлены, если 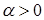 и противоположно направлены, если
и противоположно направлены, если 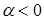 .
.
Выражение  называется линейной комбинацией векторов.
называется линейной комбинацией векторов.
Базисом в пространстве называются три любых не компланарных вектора, взятые в определенном порядке.
Базисом на плоскости называются два любых не коллинеарных вектора, взятых в определенном порядке.
Если 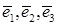 - базис в пространстве, то коэффициенты разложения вектора
- базис в пространстве, то коэффициенты разложения вектора  по базису
по базису  называются координатами
называются координатами
Каждый вектор в плоскости может быть единственным образом разложен по данному базису этой плоскости;
Каждый вектор пространства может быть единственным образом разложен по данному базису в пространстве.
Равные векторы имеют равные координаты.
При умножении вектора на число все его координаты умножаются на это число.
При сложении векторов складываются их координаты.
Прямоугольная декартова система координат.
Прямоугольной декартовой системой координат в пространстве называется точка и базис, векторы которого
а) попарно перпендикулярны (ортогональны),
б)  .
.
Точка называется началом координат. Прямые, проходящие через начало координат в направлении базисных векторов, называются осями координат (абсцисса, ордината, аппликата).
Приняты обозначения: 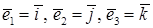 .
.
Координаты радиус-вектора точки M называются координатами точки M в данной системе координат.
Нетрудно проверить, что координаты точки в декартовой прямоугольной системе координат по абсолютной величине равны расстоянию от этой точки до координатных плоскостей. Они имеют знак (+) или (–) в зависимости от того в каком квадранте пространства она находится.
Пусть в данной прямоугольной декартовой системе координат вектор 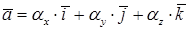 . Найти длину вектора можно по формуле
. Найти длину вектора можно по формуле
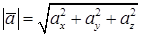 .
.
Для того чтобы найти координаты вектора нужно из координат конца вычесть координаты начала.
Пусть даны точки 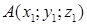 и
и 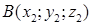 , тогда координаты вектора
, тогда координаты вектора 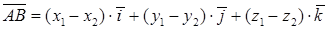
Пусть даны концы отрезка точки 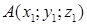 ,
, 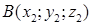 и точка
и точка 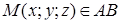 и делящая его в отношении
и делящая его в отношении 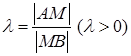 . Тогда координаты точки
. Тогда координаты точки  вычисляются по формулам
вычисляются по формулам 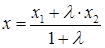 ;
;  ;
;  .
.
Следствие: Координаты середины отрезка равны среднему арифметическому координат концов отрезка.
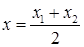 ;
; 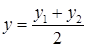 ;
; 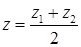 .
.
Пусть в данной прямоугольной декартовой системе координат даны векторы
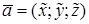 ,
, 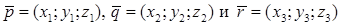 , причем векторы
, причем векторы  сами образуют базис. Вектор
сами образуют базис. Вектор  можно разложить по базису
можно разложить по базису  т.е. записать в виде
т.е. записать в виде 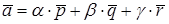
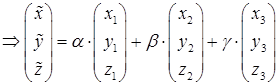 .
.
Таким образом, решение задачи сводится к решению системы линейных уравнений
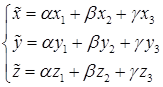 .
.
Плоскость в пространстве.
В прямоугольной декартовой системе координат каждая плоскость может быть задана линейным уравнением вида:  , которое называется «общее уравнение»
, которое называется «общее уравнение»
Уравнение плоскости, проходящей через заданную точку перпендикулярно заданному вектору, имеет вид 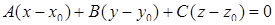 .
.
Геометрический смысл коэффициентов при неизвестных уравнения общего уравнения плоскости – координаты нормального вектора плоскости.
Если плоскость проходит через заданную точку 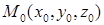 компланарно двум векторам
компланарно двум векторам  , то уравнение плоскости можно написать так:
, то уравнение плоскости можно написать так: 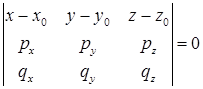 , раскрывая определитель, получим уравнение плоскости.
, раскрывая определитель, получим уравнение плоскости.
Если плоскость проходит через три заданные точки 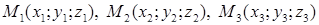 , то уравнение плоскости получим из условия
, то уравнение плоскости получим из условия 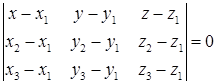
Если плоскость отрезает на координатных осях не нулевые отрезки т.е. пересекает координатные оси в точках 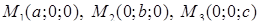 , то получим уравнение плоскости в отрезках
, то получим уравнение плоскости в отрезках
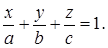
Расстояние от точки 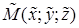 до плоскости
до плоскости  можно вычислить по формуле
можно вычислить по формуле
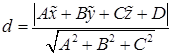 .
.
Пусть даны две плоскости 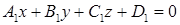 и
и  .
.
а) если плоскости пересекаются, то их нормальные векторы 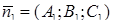 и
и 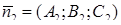 не коллинеарны, т.е.
не коллинеарны, т.е. 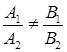 или
или 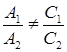 .
.
б) если плоскости параллельны (но не совпадают), то 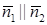 , то
, то

 .
.
в) если плоскости совпадают, то 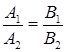
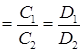 .
.
Прямая в пространстве.
В прямоугольной декартовой системе координат
Каждая прямая может быть задана, как линия пересечения двух непараллельных плоскостей
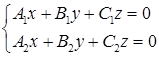
Верно обратное утверждение: каждое уравнение указанного вида при 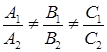 определяет прямую в пространстве.
определяет прямую в пространстве.
Однако более удобно при решении задач использовать другие уравнения.
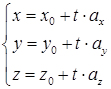 – параметрическое уравнение прямой или
– параметрическое уравнение прямой или
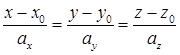 – каноническое уравнение прямой (два линейно независимых уравнения), где
– каноническое уравнение прямой (два линейно независимых уравнения), где 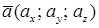 – направляющий вектор прямой, а точка
– направляющий вектор прямой, а точка 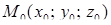 принадлежит прямой.
принадлежит прямой.
Через две заданные точки M1(x1; y1; z1), M2(x2; y2; z2) можно провести прямую, уравнение которой находится по формуле 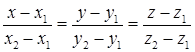
Пусть даны уравнения двух прямых.
L1: 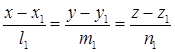 L2:
L2: 
а) прямые скрещиваются (не лежат в одной плоскости), если выполняется условие

б) прямые пересекаются если
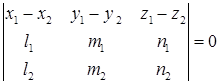 и
и  .
.
в) прямые параллельны если
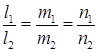 ,
, 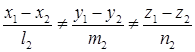 .
.
г) прямые совпадают три вектора 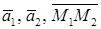 коллинеарны.
коллинеарны.
Углом между двумя прямыми называется любой из двух углов между двумя параллельными им прямыми, проходящими через произвольную точку пространства. Вычислить косинус угла можно вычислить по формуле
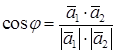 .
.
Пусть дана прямая 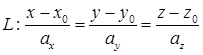 и плоскость
и плоскость
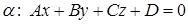
а) плоскость и прямая пересекаются если 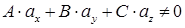 .
.
б) плоскость и прямая параллельны если
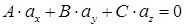 , но
, но  .
.
в) прямая лежит в плоскости если.
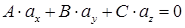 и
и 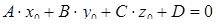 .
.
Углом между прямой и плоскостью называется, меньший из двух углов между этой прямой и ее ортогональной проекцией на эту плоскость.
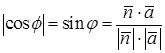 .
.
Прямая и плоскость перпендикулярны, если 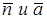 коллинеарны.
коллинеарны.
Для того чтобы найти точку пересечения прямой и плоскости.
Воспользуемся параметрическим уравнением прямой и составим систему 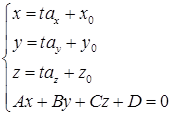
Если 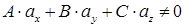 , то система имеет единственное решение, а значит общая точка находится однозначно.
, то система имеет единственное решение, а значит общая точка находится однозначно.
Прямая на плоскости.
Любая прямая на плоскости может быть задана линейным уравнением 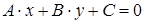 .
.
Верно и обратное утверждение: любое линейное уравнение определяет некоторую прямую.
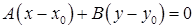 – уравнение прямой проходящей через заданную точку
– уравнение прямой проходящей через заданную точку 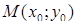 перпендикулярно заданному вектору
перпендикулярно заданному вектору 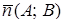 .
.
Пусть 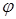 - угол, который прямая L образует с положительным направлением оси ox. Тогда уравнение прямой можно записать в виде:
- угол, который прямая L образует с положительным направлением оси ox. Тогда уравнение прямой можно записать в виде:  или
или 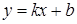 , где k называется угловым коэффициентом, а b начальной ординатой. Если выразить y из общего уравнения, то получим равенство:
, где k называется угловым коэффициентом, а b начальной ординатой. Если выразить y из общего уравнения, то получим равенство: 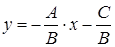 . Таким образом,
. Таким образом, 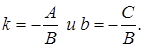
Пусть точка M0(x0; y0) принадлежит прямой L, уравнение которой 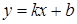 , т.е. y 0 = kx 0 + b и y – y 0 = k(x – x 0) – уравнение прямой, проходящей через заданную точку в заданном направлении.
, т.е. y 0 = kx 0 + b и y – y 0 = k(x – x 0) – уравнение прямой, проходящей через заданную точку в заданном направлении.
Пусть прямая L проходит через точку M0(x 0; y 0) параллельно заданному вектору 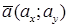 – направляющему вектору данной прямой. Тогда
– направляющему вектору данной прямой. Тогда
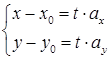 – параметрическое уравнение,
– параметрическое уравнение,
а 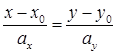 – каноническое уравнение прямой.
– каноническое уравнение прямой.
Можно написать уравнение прямой проходящей через две заданные точки 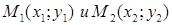 :
: 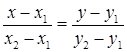 .
.
Две прямые L1 : 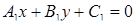 и L2 :
и L2 : 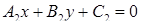 на плоскости либо пересекаются, либо параллельны, либо совпадают.
на плоскости либо пересекаются, либо параллельны, либо совпадают.
В первом случае нормальные векторы 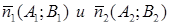 не коллинеарны; т.е.
не коллинеарны; т.е. 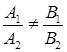 или
или  . При этом условии система
. При этом условии система 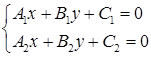
имеет единственное решение, так как главный определитель 
Если прямые L1 и L2 параллельны, то 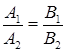 и
и 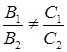
Если прямые L1 и L2 совпадают, то нетрудно видеть, что 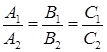 и
и
Угол между двумя прямыми L1 и L2 определяется углом между их нормальными векторами 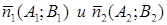 :
:  .
.
Угол между двумя прямыми может быть найден с помощью угловых коэффициентов. Рассмотрим прямые L1  и L2
и L2 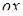
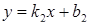 ,
,
которые составляют с координатной осью 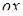 углы
углы  .
.
Если угол между прямыми L1 и L2 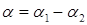 , тогда
, тогда  , или
, или 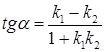 .
.
Если прямые параллельны, то 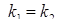 – условие параллельности прямых.
– условие параллельности прямых.
Если прямые перпендикулярны, то 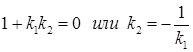 – условие перпендикулярности векторов.
– условие перпендикулярности векторов.
Пусть даны прямая L Ax + By + С = 0 и точка  не лежащая на данной прямой. Расстояние от точки до прямой можно вычислить по формуле
не лежащая на данной прямой. Расстояние от точки до прямой можно вычислить по формуле 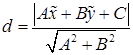 .
.
Кривые второго порядка.
Общее уравнение кривой второго порядка имеет вид
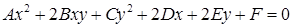
I. Эллипс.
Определение: Эллипсом называется множество точек плоскости, для каждой из которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами, есть данное число 2a, большее, чем расстояние 2c между фокусами.
Каноническое уравнение эллипса: 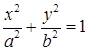 .
.
Число a называется большая полуось, b – малая полуось, причем  .
.
Из уравнения следует, что 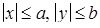 , т.е. все точки эллипса лежат внутри прямоугольника
, т.е. все точки эллипса лежат внутри прямоугольника  .
.
Эллипс имеет центр симметрии – начало координат, и две оси симметрии – координатные оси. Если a = b, то уравнение принимает вид: 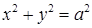 . Т.е. окружность есть частный случай эллипса.
. Т.е. окружность есть частный случай эллипса.
Отношение расстояния между фокусами 2c к длине большой полуоси 2a называется эксцентриситет и обозначается 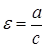 . Т.к.
. Т.к.  ; т.к.
; т.к.  т.е. эксцентриситет определяет форму эллипса.
т.е. эксцентриситет определяет форму эллипса.
II. Гипербола
Определение: Гиперболой называется множество точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек плоскости, называемых фокусами, есть данное положительное число 2a, меньшее, чем расстояние 2c между фокусами.
Уравнение 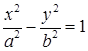 называется каноническим уравнением гиперболы. Число a называется действительная полуось, а b – мнимая полуось, причем по определению
называется каноническим уравнением гиперболы. Число a называется действительная полуось, а b – мнимая полуось, причем по определению  .
.
Из уравнения (2) следует, что  . Ось ox пересекает гиперболу в двух точках A1(–a; 0) и A2(a; 0) и называется действительной осью гиперболы. Ось oy не пересекает гиперболу и называется мнимой осью. Две прямые
. Ось ox пересекает гиперболу в двух точках A1(–a; 0) и A2(a; 0) и называется действительной осью гиперболы. Ось oy не пересекает гиперболу и называется мнимой осью. Две прямые 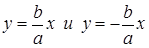 являются асимптотами гиперболы.
являются асимптотами гиперболы.
Асимптоты гиперболы являются диагоналями прямоугольника со сторонами 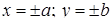 .
.
Отношение расстояния между фокусами 2c к действительной оси 2a называется эксцентриситетом гиперболы и обозначается  . Т.к.
. Т.к. 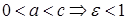 , т.е. эксцентриситет определяет форму гиперболы
, т.е. эксцентриситет определяет форму гиперболы 
Уравнение 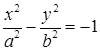 определяет гиперболу сопряженную данной. У них меняются местами действительная и мнимая оси.
определяет гиперболу сопряженную данной. У них меняются местами действительная и мнимая оси.
III. Парабола
Определение: Параболой называется множество точек плоскости, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, не проходящей через фокус, и называемой директрисой.
Расстояние от фокуса параболы до ее директрисы называется параметром (p>0). Эксцентриситет параболы принимается равным единице 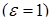 .
.
Каноническое уравнение параболы  .
.
Ось ox является осью параболы, начало координат – вершиной,  уравнение директрисы
уравнение директрисы 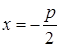 .
.
ВЫСШАЯ МАТЕМАТИКА
Учебно-методическое пособие
по выполнению контрольных работ № 1, 2, 3
Дата: 2018-11-18, просмотров: 331.