Работу стали при одноосном растяжении характеризует диаграмма зависимости растягивающих напряжений σ и относительных деформаций ε.
Связь между напряжением и удлинением образца на начальном этапе испытания следует закону Гука
s 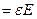 ,
,
где Е – коэффициент пропорциональности между напряжением и удлинением, носящий название модуля упругости и равный для стали 21000кН/см2
Геометрически модуль упругости представляет собой 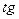
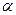 .
.
Линейная связь между напряжением и удлинением сохраняется до величины напряжений примерно 20 кН/см2 и со ответствует пределу пропорциональности sр. Несколько выше этой точки лежит предел упругости sе, соответствующий такой деформации, которая практически полностью исчезает после разгрузки образца. Предел упругости ограничивает область упругой работы материала. При дальнейшей нагрузке образца модуль упругости стали уменьшается (криволинейная часть диаграммы) и при напряжении около 24 кН/см2 становится равным нулю (начало горизонтального участка диаграммы). Это напряжение называется пределом текучести sу. В дальнейшем образец продолжает удлиняться без приложения дополнительной нагрузки, т. е. как бы «течет».
Область работы материала между напряжениями sе и sу является областью упругопластической работы. Горизонтальный участок диаграммы называется площадкой текучести. При относительном удлинении образца около 2,5% «течение» заканчивается и материал становится снова несущеспособным, он как бы самоупрочняется (область самоупрочнения).
При дальнейшем увеличении нагрузки удлинения продолжают нарастать, в образце образовывается шейка (местное сужение) и при относительном удлинении 18— 25% происходит разрыв.
Сталь при работе на сжатие в коротких элементах ведет себя так же, как и при растяжении. Значение предела текучести sу, модуля упругости Е и величина площадки текучести равны аналогичным показателям при растяжении. Однако разрушить путем сжатия короткие образцы, изготовленные из пластичной стали, не представляется возможным из-за расплющивания образца. При расчете на сжатие коротких элементов, которые не могут потерять устойчивость, расчетное сопротивление принимается более высоким чем, при растяжении. Иная картина наблюдается в длинных сжатых элементах, длина которых в несколько раз превышает ширину поперечного сечения (гибкие элементы). В этом случае элемент может потерять свою несущую способность, т. е. способность сопротивляться внешним воздействиям, не в результате разрушения материала, а в результате потери устойчивости (продольного изгиба).
Дата: 2018-11-18, просмотров: 714.