Поиск решения – это надстройка Excel, которая позволяет решать оптимизационные задачи. Если в меню Данные отсутствует команда Поиск решения, значит, необходимо загрузить эту надстройку. Выберите кнопку “ Office ” Þ Параметры Excel Þ Надстройки и активизируйте надстройку Поиск решения.

Для того чтобы решить задачу ЛП в табличном редакторе Microsoft Excel, необходимо выполнить следующие действия.

1. Ввести условие задачи:

a) создать экранную форму для ввода условия задачи:

- переменных,

- целевой функции (ЦФ),

- ограничений;

b) ввести исходные данные в экранную форму:

- коэффициенты ЦФ,

- коэффициенты при переменных в ограничениях,

- правые части ограничений;

c) ввести зависимости из математической модели в экранную форму:

- формулу для расчета ЦФ,

- формулы для расчета значений левых частей ограничений;

d) задать ЦФ (в окне Поиск решения):

- целевую ячейку,

- направление оптимизации ЦФ;

e) ввести изменяемые ячейки и ограничения (в окне Поиск решения):

- ячейки со значениями переменных,

- соотношения между правыми и левыми частями ограничений;

f) ввести параметры для решения задачи (в окне Поиск решения):

- линейная модель (для применения симплекс-метода),

- неотрицательные значения переменных.

2. Решить задачу:

a) запустить задачу на решение (в окне Поиск решения);

b) выбрать формат вывода решения (в окне Результаты поиска решения).

Одноиндексные задачи ЛП

Рассмотрим пример нахождения решения для следующей одноиндексной задачи ЛП:

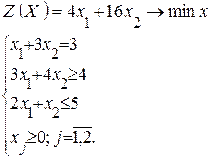
(1.1)

Ввод исходных данных

Создание экранной формы и ввод в нее условия задачи

Экранная форма для ввода условий задачи (1.1) вместе с введенными в нее исходными данными представлена на рис.1.1.

В экранной форме каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка в Excel. Имя ячейки состоит из буквы, обозначающей столбец, и цифры, обозначающей строку, на пересечении которых находится объект задачи ЛП. Так, например, переменным задачи (1.1) соответствуют ячейки B3 (х₁), C3 (х₂), коэффициентам ЦФ соответствуют ячейки B4 (с₁=4), C4 (с₂=16), правым частям ограничений соответствуют ячейки F 7 (b₁=3), F 8 (b₂=4), F 9 (b₃=5) и т. д.

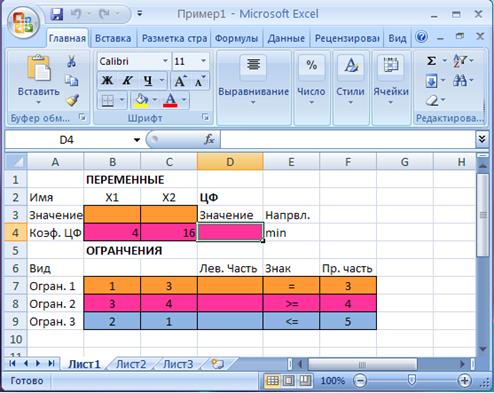
Рис.1.1. Экранная форма задачи (1.1) (курсор в ячейке D4)

Ввод зависимостей из математической модели в экранную форму

Зависимость для ЦФ

В ячейку D 4, в которой будет отображаться значение ЦФ, необходимо ввести формулу, по которой это значение будет рассчитано. Согласно (1.1) значение ЦФ определяется выражением

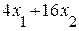
(1.2)

Используя обозначения соответствующих ячеек в Excel (см. рис.1.1), формулу для расчета ЦФ (1.2) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B 3, C 3), на соответствующую ячейку, отведенную для коэффициентов ЦФ (B 4, C 4), то есть

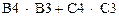
(1.3)

Чтобы задать формулу (1.3) необходимо в ячейку D 4 ввести следующее выражение и нажать клавишу Enter

где символ $ перед номером строки 3 означает, что при копировании этой формулы в другие места листа Excel номер строки 3 не изменится, а символ $ перед названием столбца B означает, что при копировании этой формулы в другие места листа Excel номер столбца B не изменится;

символ: означает, что в формуле будут использованы все ячейки, расположенные между ячейками, указанными слева и справа от двоеточия. После этого в целевой ячейке появится 0 (нулевое значение) (рис.1.2).

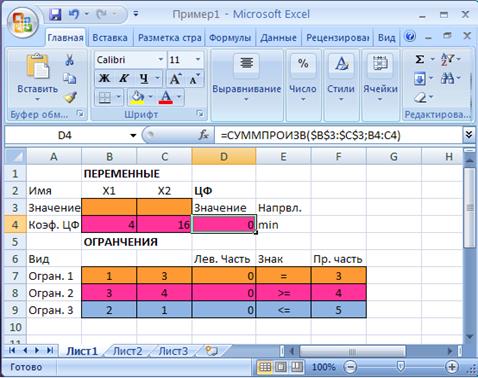
Рис.1.2. Экранная форма задачи (1.1) после ввода всех необходимых формул

(курсор в ячейке D4)

Примечание 1.1. Существует другой способ задания функций в Excel с помощью режима Вставка функций, который можно вызвать из меню Вставка или при нажатии кнопки  на стандартной панели инструментов. Так, например, формулу (1.4) можно задать следующим образом:

- курсор в поле D 4;

- нажав кнопку , вызовите окно Мастер функций – шаг 1 из 2;

- выберите в окне Категория категорию Математические;

- в окне Функция выберите функцию СУММПРОИЗВ;

- в появившемся окне СУММПРОИЗВ в строку Массив 1 введите выражение $ B $3:$ C $3, а в строку Массив 2 – выражение B 4: C 4 (рис.1.3);

- после ввода ячеек в строки Массив 1 и Массив 2 в окне СУММПРОИЗВ появятся числовые значения введенных массивов (см. рис.1.3), а в экранной форме в ячейке D 4 появится текущее значение, вычисленное по введенной формуле, то есть 0, так как в момент ввода формулы значения переменных задачи нулевые.

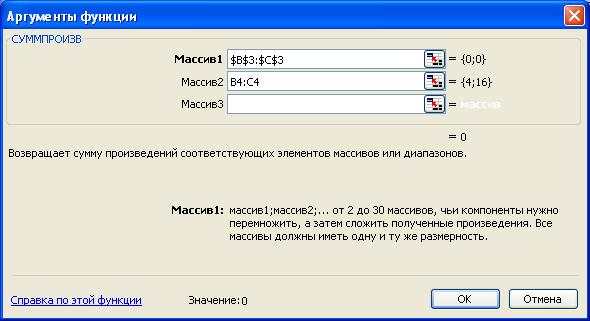
Рис.1.3. Ввод формулы для расчета ЦФ в окно СУММПРОИЗВ

Зависимости для левых частей ограничений

Левые части ограничений задачи (1.1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B 3, C 3), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (B 7, C 7 – 1-е ограничение; B 8, C 8 – 2-е ограничение и B 9, C 9 – 3-е ограничение). Формулы, соответствующие левым частям ограничений, представлены в табл.1.1.

Таблица 1.1