Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

ЛАБОРАТОРНАЯ РАБОТА №1 «РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО   ПРОГРАММИРОВАНИЯ С ИСПОЛЬЗОВАНИЕМ Microsoft Excel 2007»

 

ЦЕЛЬ РАБОТЫ

Приобретение навыков решения задач линейного программирования (ЛП) в табличном редакторе Microsoft Excel.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Для модели ЛП, соответствующей номеру вашего варианта, найдите оптимальное решение в табличном редакторе Microsoft Excel и продемонстрируйте его преподавателю.

ИНСТРУКЦИЯ ПО ИСПОЛЬЗОВАНИЮ Microsoft Excel ДЛЯ РЕШЕНИЯ ЗАДАЧ ЛП

Поиск решения – это надстройка Excel, которая позволяет решать оптимизационные задачи. Если в меню Данные отсутствует команда Поиск решения, значит, необходимо загрузить эту надстройку. Выберите кнопку “ Office ” Þ Параметры Excel Þ Надстройки и активизируйте надстройку Поиск решения.

Для того чтобы решить задачу ЛП в табличном редакторе Microsoft Excel, необходимо выполнить следующие действия.

1. Ввести условие задачи:

a) создать экранную форму для ввода условия задачи:

- переменных,

- целевой функции (ЦФ),

- ограничений;

b) ввести исходные данные в экранную форму:

- коэффициенты ЦФ,

- коэффициенты при переменных в ограничениях,

- правые части ограничений;

c) ввести зависимости из математической модели в экранную форму:

- формулу для расчета ЦФ,

- формулы для расчета значений левых частей ограничений;

d) задать ЦФ (в окне Поиск решения):

- целевую ячейку,

- направление оптимизации ЦФ;

e) ввести изменяемые ячейки и ограничения (в окне Поиск решения):

- ячейки со значениями переменных,

- соотношения между правыми и левыми частями ограничений;

f) ввести параметры для решения задачи (в окне Поиск решения):

- линейная модель (для применения симплекс-метода),

- неотрицательные значения переменных.

2. Решить задачу:

a) запустить задачу на решение (в окне Поиск решения);

b) выбрать формат вывода решения (в окне Результаты поиска решения).

Одноиндексные задачи ЛП

Рассмотрим пример нахождения решения для следующей одноиндексной задачи ЛП:

 

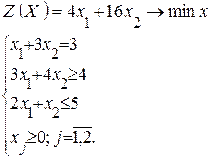
(1.1)

Ввод исходных данных

Создание экранной формы и ввод в нее условия задачи

Экранная форма для ввода условий задачи (1.1) вместе с введенными в нее исходными данными представлена на рис.1.1.

В экранной форме каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка в Excel. Имя ячейки состоит из буквы, обозначающей столбец, и цифры, обозначающей строку, на пересечении которых находится объект задачи ЛП. Так, например, переменным задачи (1.1) соответствуют ячейки B3 (х₁), C3 (х₂), коэффициентам ЦФ соответствуют ячейки B4 (с₁=4), C4 (с₂=16), правым частям ограничений соответствуют ячейки F 7 (b₁=3), F 8 (b₂=4), F 9 (b₃=5) и т. д.

 

 

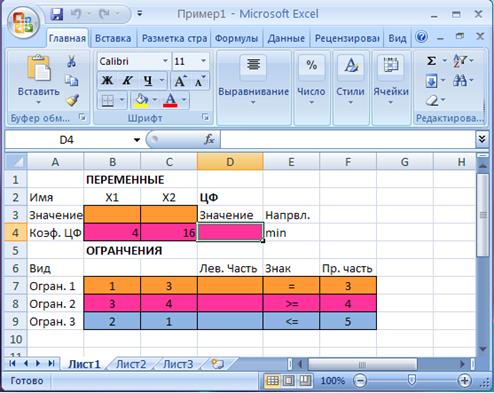
Рис.1.1. Экранная форма задачи (1.1) (курсор в ячейке D4)

Ввод зависимостей из математической модели в экранную форму

Зависимость для ЦФ

В ячейку D 4, в которой будет отображаться значение ЦФ, необходимо ввести формулу, по которой это значение будет рассчитано. Согласно (1.1) значение ЦФ определяется выражением

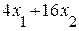
(1.2)

Используя обозначения соответствующих ячеек в Excel (см. рис.1.1), формулу для расчета ЦФ (1.2) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B 3, C 3), на соответствующую ячейку, отведенную для коэффициентов ЦФ (B 4, C 4), то есть

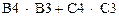
(1.3)

Чтобы задать формулу (1.3) необходимо в ячейку D 4 ввести следующее выражение и нажать клавишу Enter

=СУММПРОИЗВ($ B $3:$ C $3; B 4: C 4),

(1.4)

где символ $ перед номером строки 3 означает, что при копировании этой формулы в другие места листа Excel номер строки 3 не изменится, а символ $ перед названием столбца B означает, что при копировании этой формулы в другие места листа Excel номер столбца B не изменится;

символ: означает, что в формуле будут использованы все ячейки, расположенные между ячейками, указанными слева и справа от двоеточия. После этого в целевой ячейке появится 0 (нулевое значение) (рис.1.2).

 

 

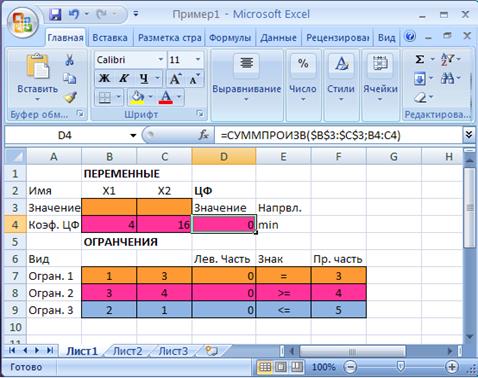
Рис.1.2. Экранная форма задачи (1.1) после ввода всех необходимых формул

(курсор в ячейке D4)

Примечание 1.1. Существует другой способ задания функций в Excel с помощью режима Вставка функций, который можно вызвать из меню Вставка или при нажатии кнопки  на стандартной панели инструментов. Так, например, формулу (1.4) можно задать следующим образом:

- курсор в поле D 4;

- нажав кнопку , вызовите окно Мастер функций – шаг 1 из 2;

- выберите в окне Категория категорию Математические;

- в окне Функция выберите функцию СУММПРОИЗВ;

- в появившемся окне СУММПРОИЗВ в строку Массив 1 введите выражение $ B $3:$ C $3, а в строку Массив 2 – выражение B 4: C 4 (рис.1.3);

- после ввода ячеек в строки Массив 1 и Массив 2 в окне СУММПРОИЗВ появятся числовые значения введенных массивов (см. рис.1.3), а в экранной форме в ячейке D 4 появится текущее значение, вычисленное по введенной формуле, то есть 0, так как в момент ввода формулы значения переменных задачи нулевые.

 

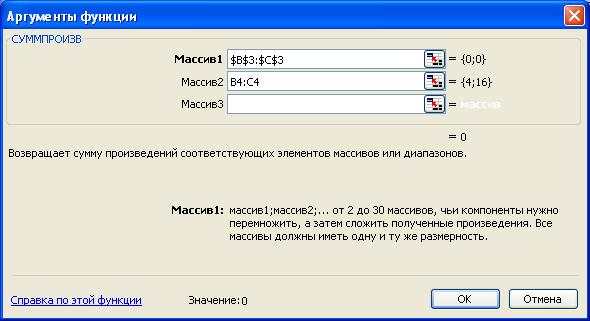
Рис.1.3. Ввод формулы для расчета ЦФ в окно СУММПРОИЗВ

Зависимости для левых частей ограничений

Левые части ограничений задачи (1.1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B 3, C 3), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (B 7, C 7 – 1-е ограничение; B 8, C 8 – 2-е ограничение и B 9, C 9 – 3-е ограничение). Формулы, соответствующие левым частям ограничений, представлены в табл.1.1.

 

Таблица 1.1

Решение задачи

Запуск задачи на решение

Запуск задачи на решение производится из окна Поиск решения путем нажатия кнопки Выполнить.

После запуска на решение задачи ЛП на экране появляется окно Результаты поиска решения с одним из сообщений, представленных на рис.1.7, 1.8 и 1.9.

 

 

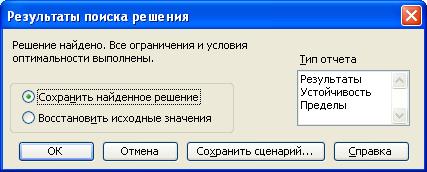
Рис.1.7. Сообщение об успешном решении задачи

 

 

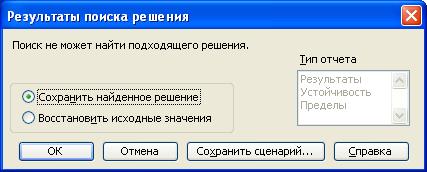
Рис.1.8. Сообщение при несовместной системе ограничений задачи

 

 

 

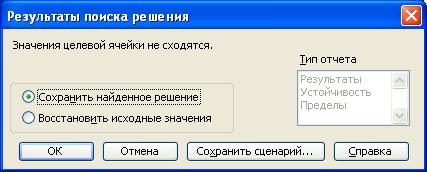
Рис.1.9. Сообщение при неограниченности ЦФ в требуемом направлении

Иногда сообщения, представленные на рис.1.8 и 1.9, свидетельствуют не о характере оптимального решения задачи, а о том, что при вводе условий задачи в Excel были допущены ошибки, не позволяющие Excel найти оптимальное решение, которое в действительности существует (см. ниже подразд.1.3.5).

Если при заполнении полей окна Поиск решения были допущены ошибки, не позволяющие Excel применить симплекс-метод для решения задачи или довести ее решение до конца, то после запуска задачи на решение на экран будет выдано соответствующее сообщение с указанием причины, по которой решение не найдено. Иногда слишком малое значение параметра Относительная погрешность не позволяет найти оптимальное решение. Для исправления этой ситуации увеличивайте погрешность поразрядно, например от 0,000001 до 0,00001 и т. д.

В окне Результаты поиска решения представлены названия трех типов отчетов: Результаты, Устойчивость, Пределы. Они необходимы при анализе полученного решения на чувствительность. Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) прямо в экранной форме просто нажмите кнопку OK . После этого в экранной форме появляется оптимальное решение задачи (рис.1.10).

 

 

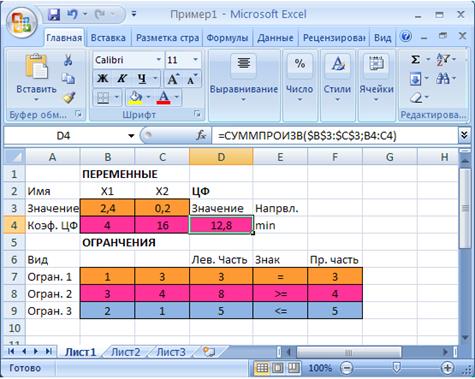
Рис.1.10. Экранная форма задачи (1.1) после получения решения

 

ЦЕЛЬ РАБОТЫ

Приобретение навыков построения математических моделей стандартных транспортных задач линейного программирования (ЛП) и решения их в Microsoft Excel.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Для транспортной модели ЛП, соответствующей номеру вашего варианта, найдите оптимальное решение в табличном редакторе Microsoft Excel и продемонстрируйте его преподавателю.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Ввод исходных данных

В конкретном примере осуществляется ввод мощностей четырех поставщиков (ячейки А10:А13), потребности регионов в их продукции (В9:Е9), а также удельные затраты по доставке груза от конкретного поставщика потребителю (блок В10:Е13) (рис. 2.1).

 

 

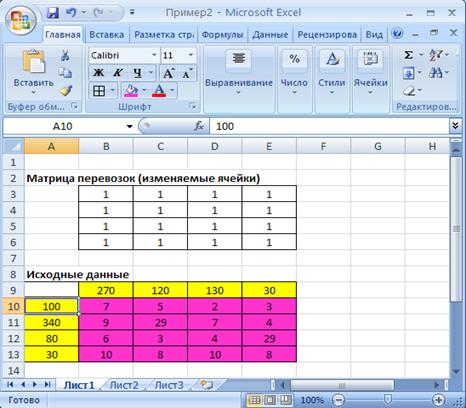
Рис.2.1. Экранная форма задачи (2.1)

 

Ввод граничных условий

Ввод условий реализации мощностей поставщиков

Необходимо выполнить следующие действия:

- поместить курсор в ячейку A3;

- выбрать знак S;

- выделить необходимые для суммирования ячейки ВЗ:ЕЗ;

- нажать Enter для подтверждения ввода формулы для суммирования (см.рис.2.2).

Аналогичные действия выполнить для ячеек А4, А5, А6, т. е. ввести условия реализации мощностей всех поставщиков (для всех строк).

Эти действия можно реализовать иначе:

- поместить курсор в ячейку A3;

- выбрать команду Копировать, т. е. скопировать в буфер формулу, введенную для ячейки A3;

- выделить ячейки А4:А6;

- выбрать команду Вставить, тем самым из буфера будет вставлена формула для суммирования в А4:А6.

 

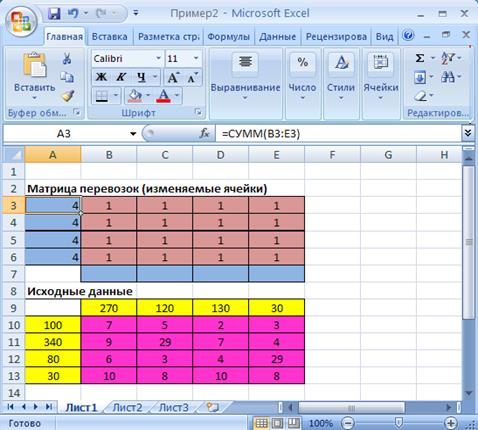
Рис.2.2. Экранная форма задачи (2.1) после суммирования ячеек B 3: E 3 (курсор в ячейке A 3)

 

Ввод условий удовлетворения запросов потребителей

Для этого необходимо выполнить следующие действия:

- поместить курсор в ячейку В7;

- выбрать знак S, при этом автоматически выделяется весь столбец B 3: B 6;

- нажать Enter для подтверждения суммирования показателей выделенного столбца (см.рис.2.3).

Эту же последовательность действий выполнить для ячеек С7 и Е7 или проделать следующее:

- поместить курсор в ячейку С7;

- выбрать команду Копировать;

- выделить ячейки С7:Е7;

- выбрать команду Вставить.

 

 

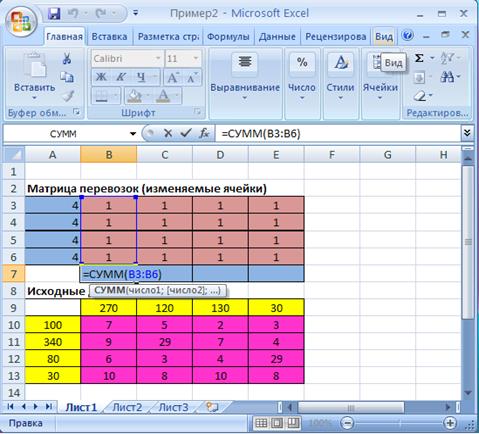
Рис.2.3. Экранная форма задачи (2.1) после суммирования ячеек B 3: B 6 (курсор в ячейке B 7)

 

Эту же последовательность действий выполнить для ячеек С7:Е7 или проделать следующее:

- поместить курсор в ячейку С7;

- выбрать команду Копировать;

- выделить ячейки С7:Е7;

- выбрать команду Вставить.

Таким образом, введены ограничения для всех поставщиков и всех потребителей (см.рис.2.4).

 

 

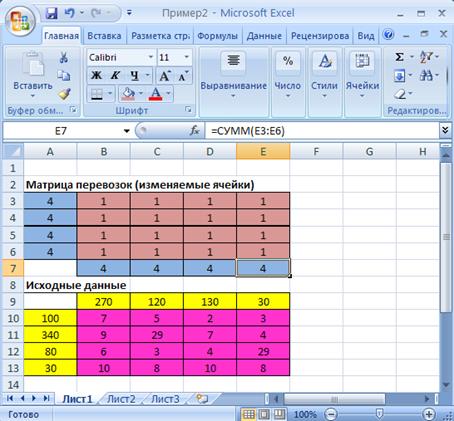
Рис.2.4. Экранная форма задачи (2.1) после введения всех ограничений

 

Назначение целевой функции

Для вычисления значения целевой функции, соответствующей минимальным суммарным затратам на доставку груза, необходимо зарезервировать ячейку и ввести формулу для ее вычисления:

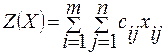
Для этого необходимо произвести следующие действия:

- поместить курсор в ячейку В15 (после решения задачи в данной ячейке будет находиться значение целевой функции);

- запустить Мастер функций (значок f_x );

- в окне Категория выбрать Математические;

- в окне Функция выбрать СУММПРОИЗВ;

- нажать кнопку ОК;

- в окне СУММПРОИЗВ указать адреса массивов, элементы которых обрабатываются этой функцией.

Целевая функция в задаче представляет собой произведение удельных затрат на доставку груза (расположенных в блоке ячеек В10÷Е13) и объемов поставок для каждого потребителя (содержимое ячеек ВЗ÷Е6). Для этого необходимо:

- в поле Массив 1 указать адреса ВЗ:Е6;

- в поле Массив 2 указать адреса В10:Е13;

- нажать кнопку ОК — подтверждение окончания ввода адресов массивов (см.рис.2.5.).

 

 

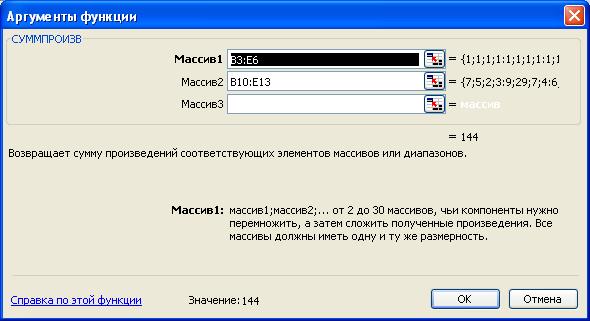
Рис.2.5. Ввод формулы для расчета ЦФ в окно Мастер функций

 

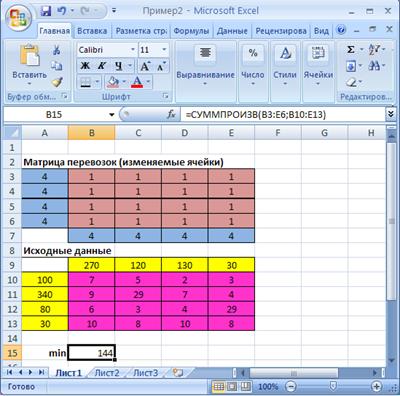
Рис.2.6. Экранная форма задачи (2.1) после ввода всех необходимых формул

 

В поле ячейки В15 появится числовое значение, равное произведению единичных поставок на удельные коэффициенты затрат по доставке грузов (в данной задаче — это число 144) (рис. 2.6.).

 

Ввод ограничений задачи

В матрицу перевозок, содержащую исходные данные по задаче, необходимо ввести условие реализации мощностей всех поставщиков (рис. 2.7):

 

 

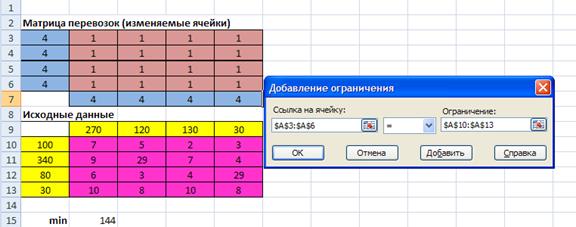
Рис.2.7. Добавление ограничений для поставщиков

 

- выбрать Добавить ограничения;

- в поле Ссылка на ячейку ввести адреса $А$3:$А$6;

- в среднем поле установить знак =;

- в поле Ограничение установить адреса $А$10:$А$13;

- для подтверждения введенного условия нажать кнопку ОК.

Далее вводится ограничение, которое реализует условие удовлетворения мощностей всех потребителей (рис. 2.8):

 

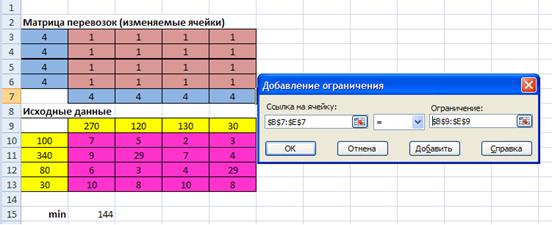
Рис.2.8. Добавление ограничений для потребителей

- выбрать Добавить ограничения;

- в поле Ссылка на ячейку ввести адреса $В$7:$Е$7;

- в поле знака выбрать знак =;

- в поле Ограничение установить адреса $В$9:$Е$9;

- нажать кнопку ОК;

 

 

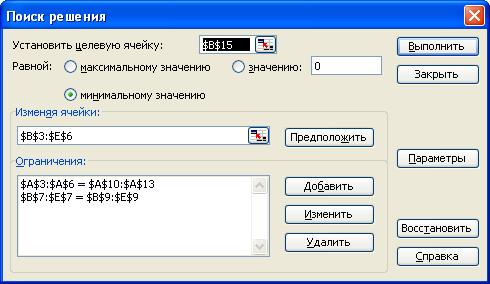
Рис.2.9. Ввод зависимостей из математической модели

- после этого надо вернуться в поле Поиск решения;

- после ввода всех ограничений ввести ОК. На экране появится окно Поиск решения с введенными ограничениями (рис. 2.9).

 

Ввод параметров

С помощью окна Параметры можно вводить условия для решения оптимизационных задач (см.рис.2.10.). В нашей задаче следует установить флажок Неотрицательные значения и флажок Линейная модель. Нажать кнопку ОК. Опять появится диалоговое окно Поиск решения. Далее необходимо:

- щелкнуть Параметры;

- выбрать переключатель Линейная модель;

- выбрать переключатель Неотрицательные значения (так как объемы поставок груза не могут быть отрицательными);

- нажать кнопку ОК. После этого произойдет переход в поле Поиск решения;

- нажать кнопку Выполнить.

 

 

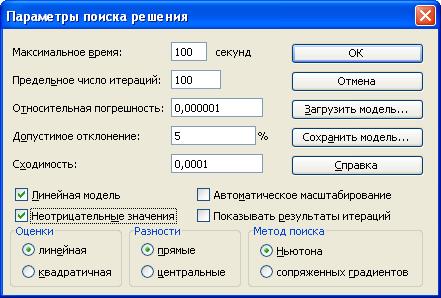
Рис.2.10. Параметры поиска решения транспортной задачи

 

Решение

Решение задачи выполняется сразу же после ввода данных, когда на экране находится диалоговое окно Поиск решения. Нажать кнопку Выполнить. На экране появится диалоговое окно Результаты поиска решения (рис.2.11).

 

 

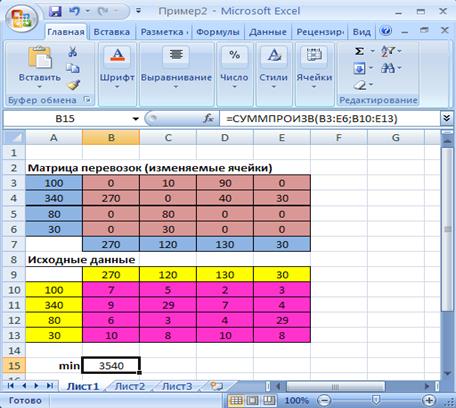
Рис.2.11. Диалоговое окно Результаты поиска решения

В результате нами был получен оптимальный план перевозок (табл.2.3).:

 

Таблица 2.3

Матрица перевозок (изменяемые ячейки)
100	0	10	90	0
340	270	0	40	30
80	0	80	0	0
30	0	30	0	0
	270	120	130	30

 

 

План перевозок означает, что:

Х₁₂ = 10 ед. груза следует перевезти от поставщика 1 потребителю 2;

Х₁₃ = 90 ед. груза следует перевезти от поставщика 1 потре­бителю 3;

X₂₁ = 270 ед. груза следует перевезти от поставщика 2 потреби­телю 1;

Х₂₃ = 40 ед. груза следует перевезти от поставщика 2 потребите­лю 3;

Х₂₄ = 30 ед. груза следует перевезти от поставщика 2 потреби­телю 4;

Х₃₂ = 80 ед. груза следует перевезти от поставщика 3 потреби­телю 2;

Х₄₂ = 30 ед. груза следует перевезти от поставщика 4 потреби­телю 2.

Общая стоимость перевозок = 3540.

 

ВАРИАНТЫ

Используя MS Excel, найти решение для модели ЛП, соответствующей заданному варианту (табл.3.1.).

Таблица 3.1

Варианты задач к лабораторной работе №1

№ варианта	Математическая модель
1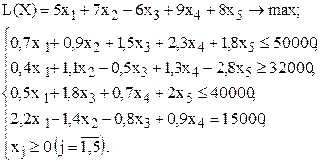
2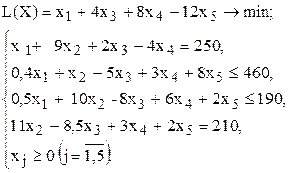
3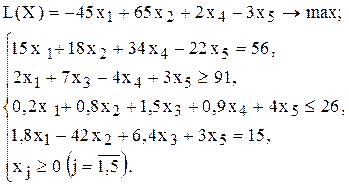
4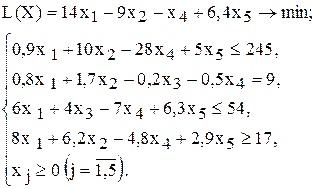
5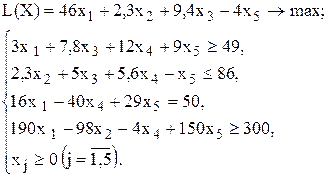
6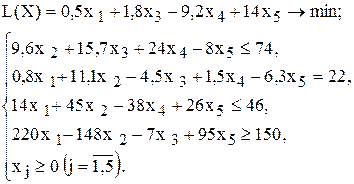
7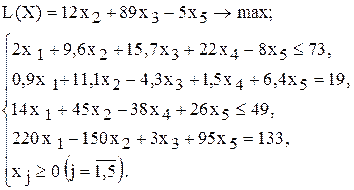
8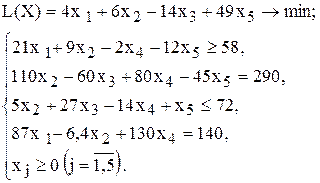
9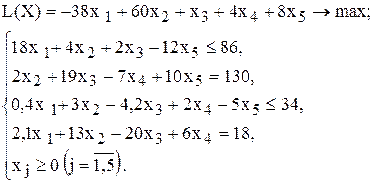
10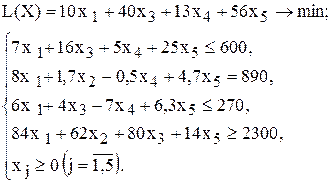
11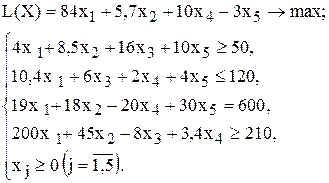
12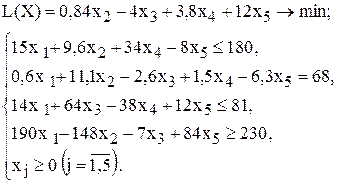

ВАРИАНТЫ

Используя MS Excel, найти решение ТЗ, соответствующей заданному варианту (табл.3.2.).

Однородный груз, имеющийся в m пунктах отправления (производства) А₁, А₂, ..., А_m соответственно в количествах а₁, а₂, ..., а_m единиц, требуется доставить в каждый из n пунктов назначения (потребления) В₁, В₂, ..., В_n соответственно в количествах b₁, b₂, …, b_n единиц. Стоимость перевозки с_ij (тариф) единицы продукции из А_i в B_j известна для всех маршрутов. Требуется составить такой план перевозок, при котором весь груз из пунктов отправления вывозится и запросы всех пунктов потребления удовлетворяются.

Таблица 3.2

Варианты задач к лабораторной работе №2

№ варианта	Математическая модель
1	Мощность поставщиков Мощность потребителей 10 20 10 15 2 3 4 1 11 6 10 3 8 9 3 21 4 1 2
2	Мощность поставщиков Мощность потребителей 20 12 5 8 15 15 1 0 3 4 2 25 5 1 2 3 3 20 4 8 1 4 3
3	Мощность поставщиков Мощность потребителей 1000 1100 900 800 3 5 6 700 7 2 4 1000 4 3 5 500 6 4 7
4	Мощность поставщиков Мощность потребителей 25 10 20 30 15 40 5 3 4 6 4 20 3 4 10 5 7 40 4 6 9 3 4
5	Мощность поставщиков Мощность потребителей 30 80 60 110 60 6 8 15 4 130 9 15 2 3 90 6 12 7 1
6	Мощность поставщиков Мощность потребителей 120 80 60 100 2 4 2 70 5 5 6 70 4 6 3 20 6 8 1
7	Мощность поставщиков Мощность потребителей 310 70 120 160 140 9 5 11 8 160 8 6 8 12 180 7 10 9 15 30 10 9 10 10 150 9 12 5 6
8	Мощность поставщиков Мощность потребителей 60 40 120 100 70 4 8 1 6 80 3 5 3 4 90 2 6 4 3 80 1 4 5 3
9	Мощность поставщиков Мощность потребителей 70 30 20 40 90 1 3 4 5 30 5 3 1 2 40 2 1 4 2
10	Мощность поставщиков Мощность потребителей 210 170 220 150 200 350 3 12 9 1 7 330 2 4 11 2 10 270 7 14 12 5 8
11	Мощность поставщиков Мощность потребителей 100 140 100 60 100 5 4 3 2 60 2 3 5 6 80 3 2 4 3 160 4 1 2 4
12	Мощность поставщиков Мощность потребителей 100 125 325 250 100 200 5 8 7 10 3 450 4 2 2 5 6 250 7 3 5 9 2

 

Используя MS Excel, найти решение ТЗ, соответствующей заданному варианту (табл.3.3.).

Однородный груз, имеющийся в m пунктах отправления (производства) А₁, А₂, ..., А_m соответственно в количествах а₁, а₂, ..., а_m единиц, требуется доставить в каждый из n пунктов назначения (потребления) В₁, В₂, ..., В_n соответственно в количествах b₁, b₂, …, b_n единиц. Стоимость перевозки с_ij (тариф) единицы продукции из А_i в B_j известна для всех маршрутов. Требуется составить такой план перевозок, при котором бы полностью удовлетворялся спрос всех потребителей, при этом хватало бы запасов поставщиков и суммарные затраты были бы минимальными.

Таблица 3.3

Варианты задач к лабораторной работе №2

№ варианта	Математическая модель
1	Мощность поставщиков Мощность потребителей 100 200 200 300 400 100 1 3 4 1 3 200 5 4 5 7 5 400 4 9 5 10 9 200 7 7 5 8 13 100 12 10 8 11 6
2	Мощность поставщиков Мощность потребителей 11 11 11 16 11 15 3 4 5 15 24 15 19 2 22 4 13 15 20 27 1 17 19
3	Мощность поставщиков Мощность потребителей 200 200 300 300 100 300 4 6 3 4 1 200 7 3 5 2 2 100 5 3 2 4 4 100 2 3 4 6 5 200 1 4 4 3 3
4	Мощность поставщиков Мощность потребителей 8 9 13 8 12 9 5 15 3 6 10 11 23 8 13 27 12 14 30 1 5 24 25
5	Мощность поставщиков Мощность потребителей 300 200 300 100 400 300 3 4 3 1 5 200 2 3 5 6 8 100 1 2 3 3 4 200 4 5 7 9 9 300 5 6 8 4 7
6	Мощность поставщиков Мощность потребителей 40 30 20 50 60 2 4 5 1 70 2 3 9 4 50 8 4 2 5
7	Мощность поставщиков Мощность потребителей 100 300 300 300 600 300 4 2 2 5 3 600 3 3 4 5 5 100 1 2 3 4 6 300 2 6 1 1 8 600 3 4 5 5 9
8	Мощность поставщиков Мощность потребителей 40 130 110 50 180 5 3 12 4 70 2 3 9 5 20 7 5 9 6
9	Мощность поставщиков Мощность потребителей 100 150 150 100 100 50 3 4 5 4 6 100 1 5 7 1 5 150 4 6 6 3 4 100 2 7 4 7 2 100 1 9 6 3 2
10	Мощность поставщиков Мощность потребителей 270 120 60 90 180 6 10 3 18 130 5 4 6 7 140 8 5 3 7 30 5 9 5 6
11	Мощность поставщиков Мощность потребителей 50 100 100 200 200 50 1 4 5 6 1 100 2 2 2 5 5 150 3 6 8 3 4 200 4 7 9 4 8 100 5 2 2 7 9
12	Мощность поставщиков Мощность потребителей 190 130 65 45 110 210 2 5 6 7 4 130 3 3 5 8 3 60 5 10 7 10 6

 

ЛАБОРАТОРНАЯ РАБОТА №1 «РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО   ПРОГРАММИРОВАНИЯ С ИСПОЛЬЗОВАНИЕМ Microsoft Excel 2007»

 

ЦЕЛЬ РАБОТЫ

Приобретение навыков решения задач линейного программирования (ЛП) в табличном редакторе Microsoft Excel.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Для модели ЛП, соответствующей номеру вашего варианта, найдите оптимальное решение в табличном редакторе Microsoft Excel и продемонстрируйте его преподавателю.