Задание 1.Для заданных матрицА, В и С найти матрицу D:
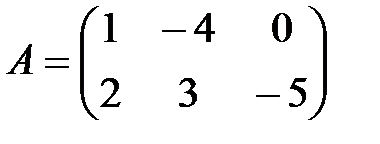 ,
, 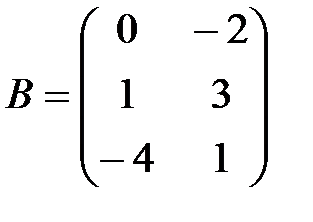 ,
, 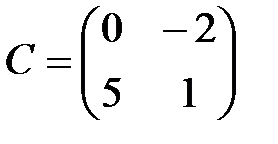 ,
, 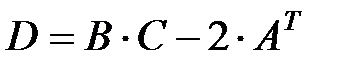 .
.
Задание 2.Вычислить определители:
а) 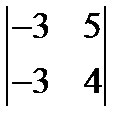 ; б)
; б) 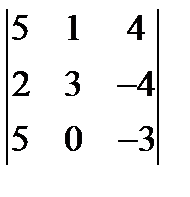 ; в)
; в) 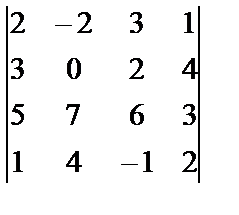 .
.
Задание 3. Для заданной матрицы  найти матрицу
найти матрицу 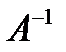
Задание 4. Решить систему уравнений методом Крамера и методом Гаусса.
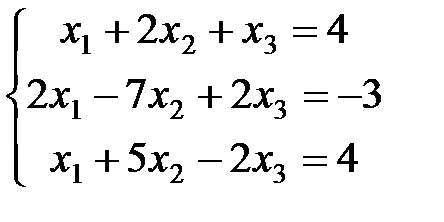 .
.
Тема 2.2. Векторная алгебра.
Задание 1. Найти угол 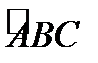 в треугольнике
в треугольнике  ,
,

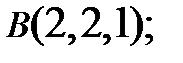
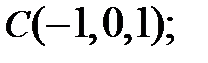 .
.
Задание 2.Найти площадь треугольника  , если
, если

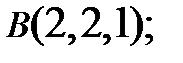
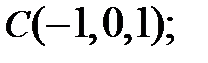 .
.
Задание 3. Лежат ли точки 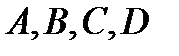 в одной плоскости, если
в одной плоскости, если
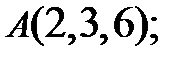
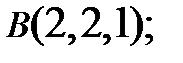
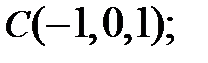
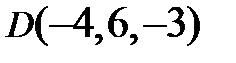
Тема 2.3. Аналитическая геометрия
Задание 1. Найти проекцию точки Р(2, –5,7) на прямую, проходящую через точки М1(4, 5, 6) и М2(–2, –17, –8).
Тема 3.1. Предел и непрерывность функции
Задание 1.Вычислить пределы.
а) 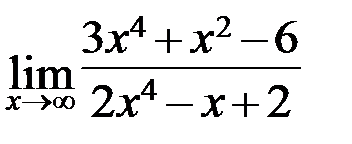 ; б)
; б) 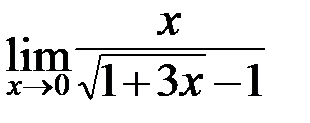 ;
;
в) 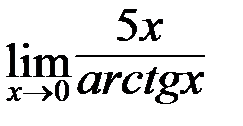 ; г)
; г) 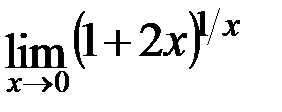 .
.
Тема 3.2. Производная функции и ее свойства
Задание 1.Найти производные функций:
а) 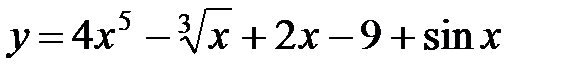 ; б)
; б) 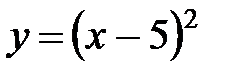 ; в)
; в)  ;
;
г) 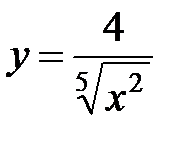 ; д)
; д) 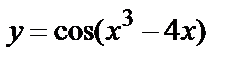 ; е)
; е) 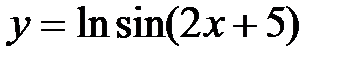 .
.
Задание 2.Найти 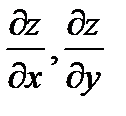 , если
, если 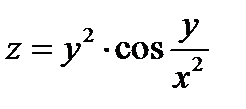
Задание 3. Провести полное исследование функций 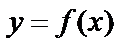
и построить графики функций:
а) 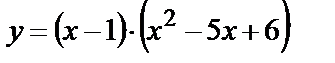 ; б)
; б) 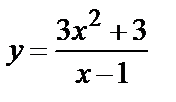 .
.
6.2. Задания и методические указания по организации самостоятельной работы студента
Расчетно-графические работы
Варианты расчетно-графической работы
Вариант №1
1. Вычислить определитель:  .
.
2. Найти АВ–ВА, где: 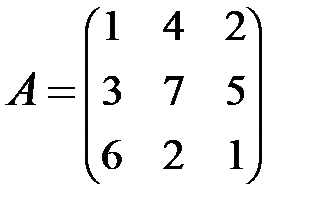 ;
; 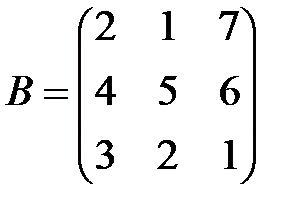 .
.
3. Найти А-1, где:  , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
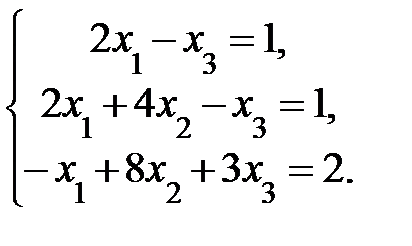 Сделать проверку.
Сделать проверку.
5. Три стороны треугольника АВС заданы уравнениями:
(АВ): х-3у-23=0; (ВС): 7х+9у+19=0; (АС): 4х+3у+13=0. Составить уравнение высоты, проведенной из вершины В и уравнение медианы, проведенной из вершины А.
6. Даны координаты вершин пирамиды 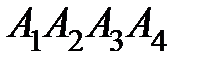 .
.
Найти: 1) длину ребра 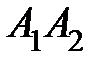 ; 2) угол между ребрами
; 2) угол между ребрами 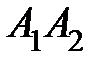 и
и  ; 3) угол между ребром
; 3) угол между ребром  и гранью
и гранью  ; 4) площадь грани
; 4) площадь грани  ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
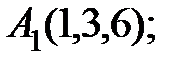
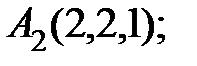
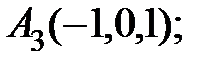
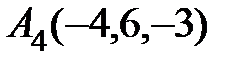 .
.
7. Найти точкуВ, симметричную точке А(1, 3, –4) относительно плоскости 3х+у–2z=0.
Вариант №2
1. Вычислить определитель: 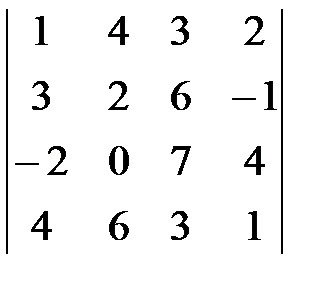 .
.
2. Найти АВ–ВА, где: 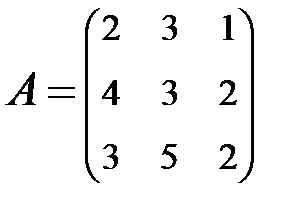 ;
; 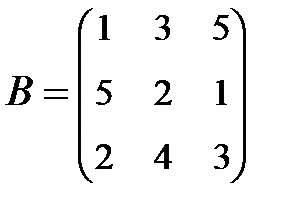 .
.
3. Найти А-1, где: 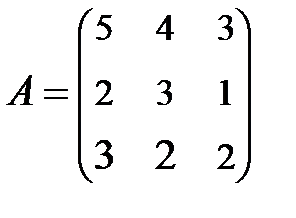 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
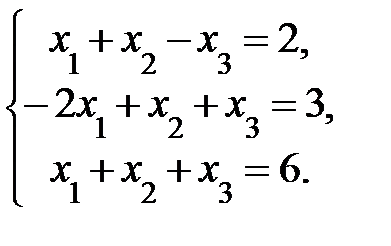 Сделать проверку.
Сделать проверку.
5. Даны уравнения одной из сторон ромба 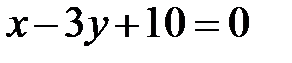 и одной из его диагоналей
и одной из его диагоналей 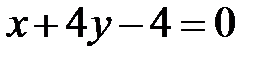 ; диагонали ромба пересекаются в точке
; диагонали ромба пересекаются в точке  .
.
Найти уравнения остальных сторон ромба.
6. Даны координаты вершин пирамиды 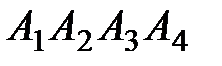 .
.
Найти: 1) длину ребра 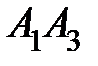 ; 2) угол между ребрами
; 2) угол между ребрами 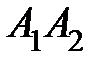 и
и 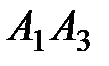 ; 3) угол между ребром
; 3) угол между ребром 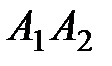 и гранью
и гранью 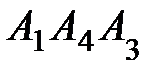 ; 4) площадь грани
; 4) площадь грани 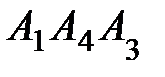 ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
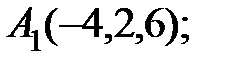
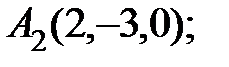
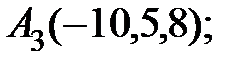
 .
.
7. Найти точку М, симметричную точке N(1, 3, 5) относительно плоскости 2х–у–3z+5=0.
Вариант №3
1. Вычислить определитель:  .
.
2. Найти АВ–ВА, где:  ;
;  .
.
3. Найти А-1, где: 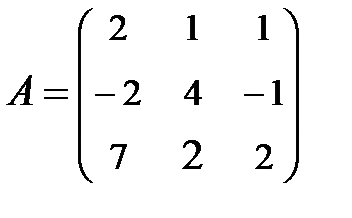 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
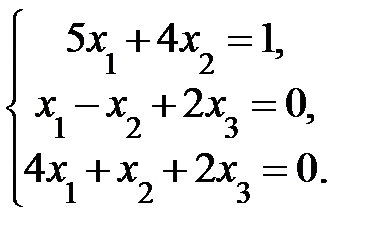 Сделать проверку.
Сделать проверку.
5. Даны две вершины  и
и  и точка
и точка 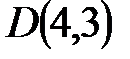 пересечения высот треугольника. Составить уравнения его сторон.
пересечения высот треугольника. Составить уравнения его сторон.
6. Даны координаты вершин пирамиды 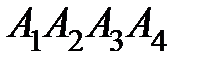 .
.
Найти: 1) длину ребра 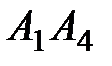 ; 2) угол между ребрами
; 2) угол между ребрами 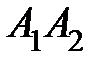 и
и 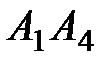 ; 3) угол между ребром
; 3) угол между ребром  и гранью
и гранью  ; 4) площадь грани
; 4) площадь грани  ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
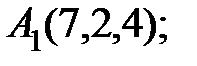
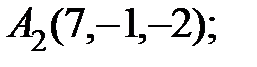
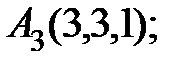
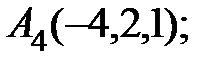
7. Найти проекцию точки Р(2, –5,7) на прямую, проходящую через точки М1(4, 5, 6) и М2(–2, –17, –8).
Вариант №4
1. Вычислить определитель: 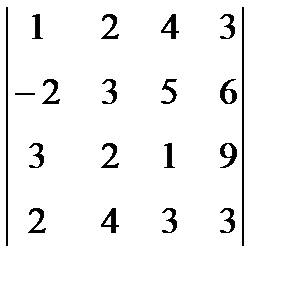 .
.
2. Найти АВ–ВА, где: 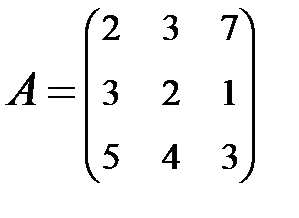 ;
;  .
.
3. Найти А-1, где: 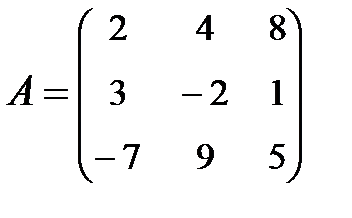 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
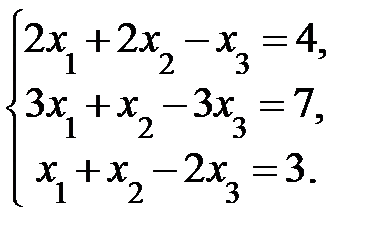 Сделать проверку.
Сделать проверку.
5. Уравнения двух сторон параллелограмма 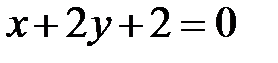 и
и 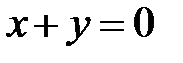 , а уравнение одной из его диагоналей
, а уравнение одной из его диагоналей 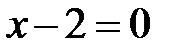 .Найти координаты вершин параллелограмма.
.Найти координаты вершин параллелограмма.
6. Даны координаты вершин пирамиды 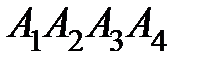 .
.
Найти: 1) длину ребра 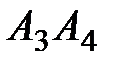 ; 2) угол между ребрами
; 2) угол между ребрами 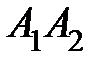 и
и 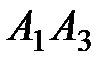 ; 3) угол между ребром
; 3) угол между ребром  и гранью
и гранью  ; 4) площадь грани
; 4) площадь грани 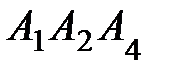 ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
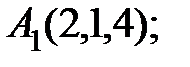
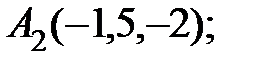
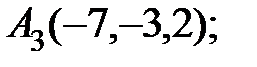
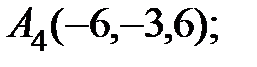
7. Найти точку Q, симметричную точке Р(4, 1, 6) относительно прямой
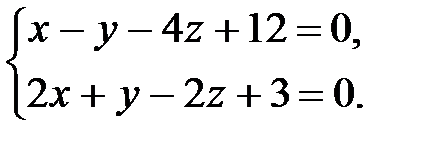
Вариант №5
1. Вычислить определитель: 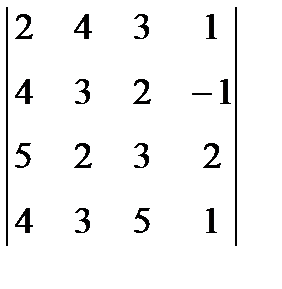 .
.
2. Найти АВ–ВА, где: 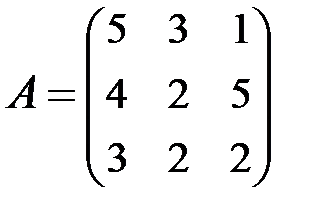 ;
; 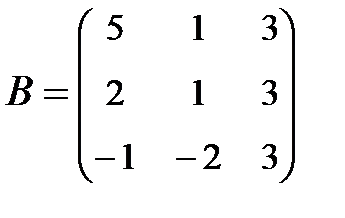 .
.
3. Найти А-1, где: 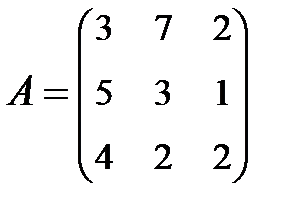 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
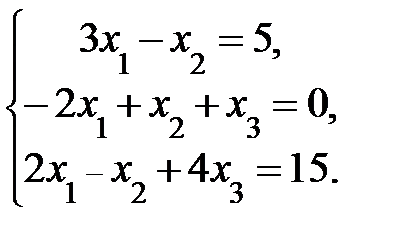 Сделать проверку.
Сделать проверку.
5. Три стороны треугольника  заданы уравнениями
заданы уравнениями 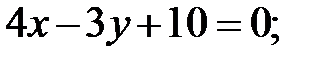
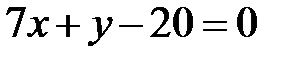 и
и 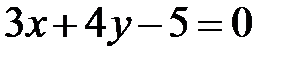 . Написать уравнение высоты и биссектрисы, проведенных из вершины
. Написать уравнение высоты и биссектрисы, проведенных из вершины 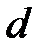 .
.
6. Даны координаты вершин пирамиды 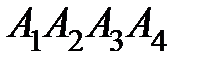 .
.
Найти: 1) длину ребра  ; 2) угол между ребрами
; 2) угол между ребрами  и
и  ; 3) угол между ребром
; 3) угол между ребром 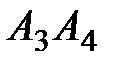 и гранью
и гранью  ; 4) площадь грани
; 4) площадь грани  ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
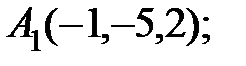
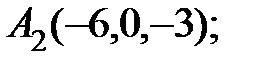
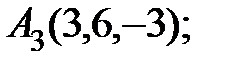
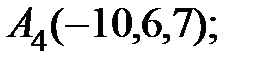
6. Найти точку Q, симметричную точке Р(2, –5, 7) относительно прямой 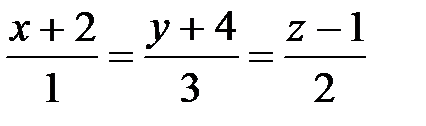
Вариант №6
1. Вычислить определитель: 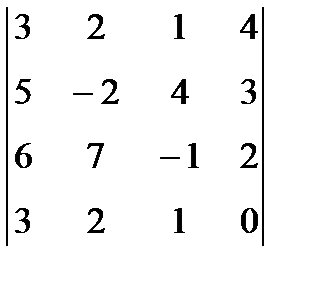 .
.
2. Найти АВ–ВА, где: 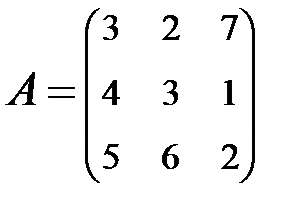 ;
; 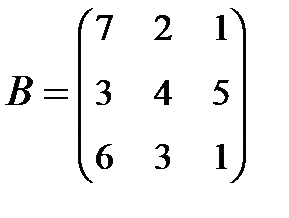 .
.
3. Найти А-1, где: 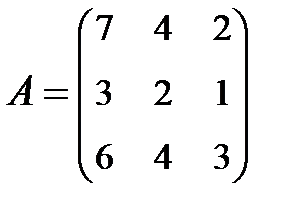 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
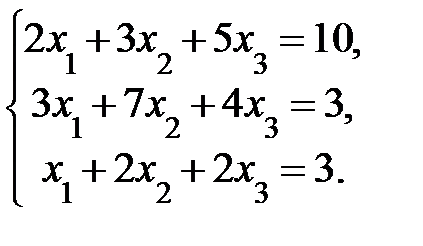 Сделать проверку.
Сделать проверку.
5. Даны вершины 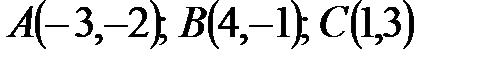 трапеции
трапеции 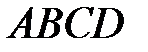
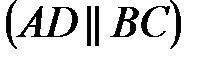 . Известно, что диагонали трапеции взаимно перпендикулярны. Найти координаты вершины
. Известно, что диагонали трапеции взаимно перпендикулярны. Найти координаты вершины 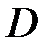 этой трапеции.
этой трапеции.
6. Даны координаты вершин пирамиды 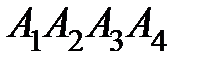 .
.
Найти: 1) длину ребра 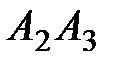 ; 2) угол между ребрами
; 2) угол между ребрами 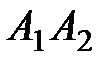 и
и 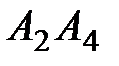 ; 3) угол между ребром
; 3) угол между ребром 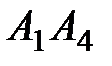 и гранью
и гранью 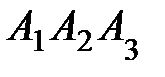 ; 4) площадь грани
; 4) площадь грани  ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
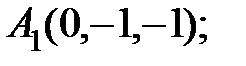
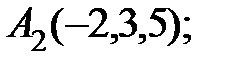

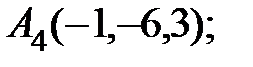
7. Найти проекцию точки А(2, 0, 3) на прямую 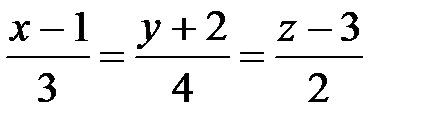 .
.
Вариант №7
1. Вычислить определитель:  .
.
2. Найти АВ–ВА, где: 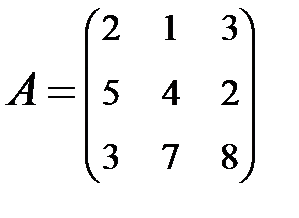 ;
; 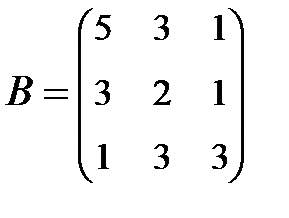 .
.
3. Найти А-1, где: 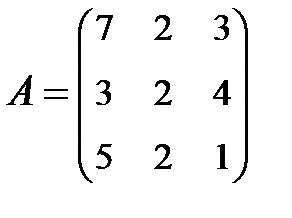 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
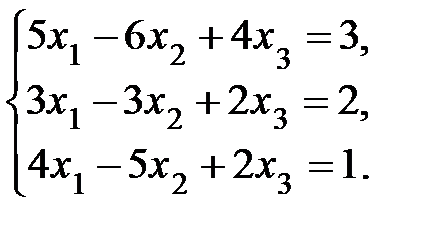 Сделать проверку.
Сделать проверку.
5. Даны уравнения двух сторон треугольника 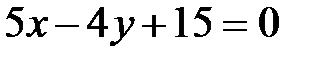 и
и 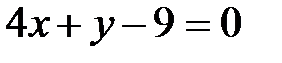 . Его медианы пересекаются в точке
. Его медианы пересекаются в точке  .Составить уравнение третьей стороны треугольника.
.Составить уравнение третьей стороны треугольника.
6. Даны координаты вершин пирамиды 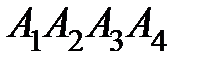 .
.
Найти: 1) длину ребра  ; 2) угол между ребрами
; 2) угол между ребрами 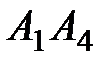 и
и 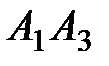 ; 3) угол между ребром
; 3) угол между ребром 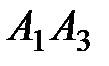 и гранью
и гранью 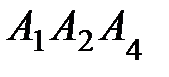 ; 4) площадь грани
; 4) площадь грани 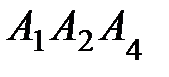 ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.

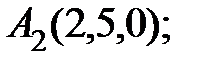

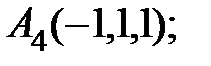
7. Найти проекцию точки А(1, –1, 2) на плоскость х+у+2z–3=0.
Вариант №8
1. Вычислить определитель: 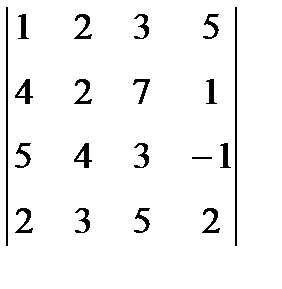 .
.
2. Найти АВ–ВА, где: 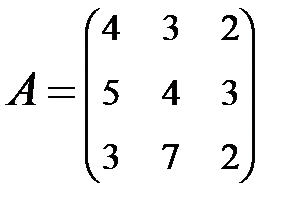 ;
; 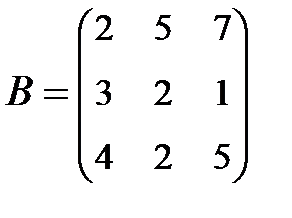 .
.
3. Найти А-1, где: 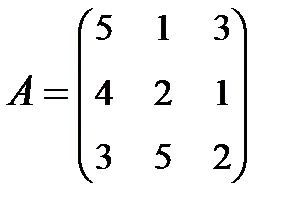 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
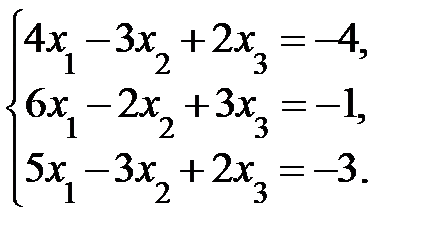 Сделать проверку.
Сделать проверку.
5. Даны две вершины 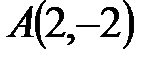 и
и 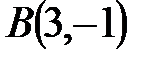 и точка
и точка 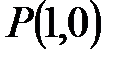 пересечения медиан треугольника
пересечения медиан треугольника 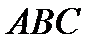 . Составить уравнение высоты треугольника, проведенной через третью вершину С.
. Составить уравнение высоты треугольника, проведенной через третью вершину С.
6. Даны координаты вершин пирамиды 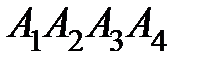 .
.
Найти: 1) длину ребра 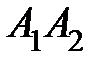 ; 2) угол между ребрами
; 2) угол между ребрами 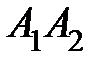 и
и  ; 3) угол между ребром
; 3) угол между ребром  и гранью
и гранью  ; 4) площадь грани
; 4) площадь грани  ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
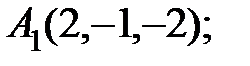

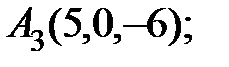
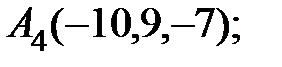
7. Найти проекцию точки М(0, –3, –2) на прямую 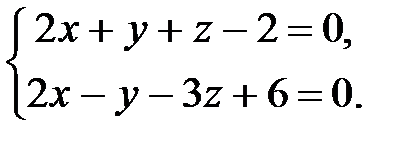
Вариант №9
1. Вычислить определитель: 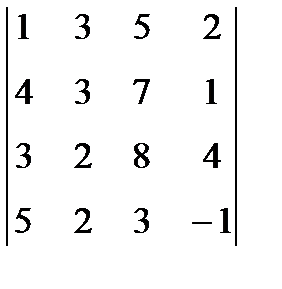 .
.
2. Найти АВ–ВА, где: 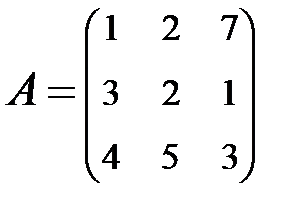 ;
; 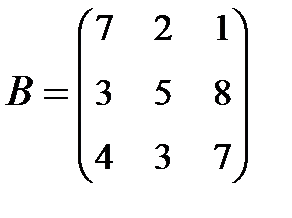 .
.
3. Найти А-1, где: 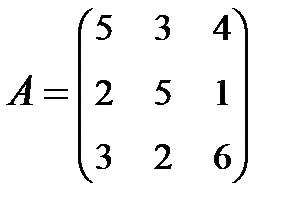 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
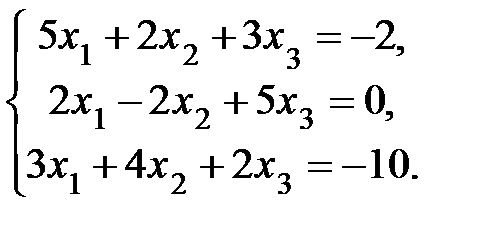 Сделать проверку.
Сделать проверку.
5. Уравнения двух высот треугольника 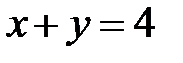 и
и  , и одна из его вершин А(0;2). Составить уравнение сторон треугольника.
, и одна из его вершин А(0;2). Составить уравнение сторон треугольника.
6. Даны координаты вершин пирамиды 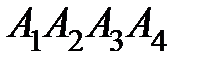 .
.
Найти: 1) длину ребра 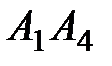 ; 2) угол между ребрами
; 2) угол между ребрами 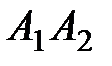 и
и 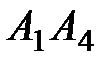 ; 3) угол между ребром
; 3) угол между ребром 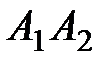 и гранью
и гранью 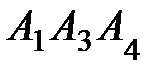 ; 4) площадь грани
; 4) площадь грани 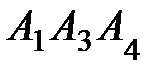 ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
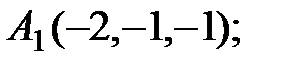
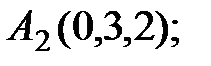
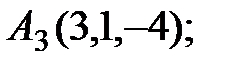
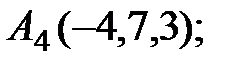
7. Найти проекцию точки М(3, 3, 3) на прямую 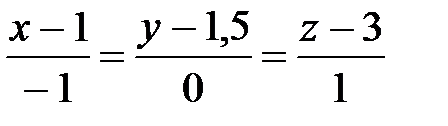 .
.
Вариант №10
1. Вычислить определитель: 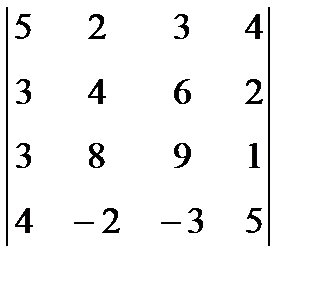 .
.
2. Найти АВ–ВА, где: 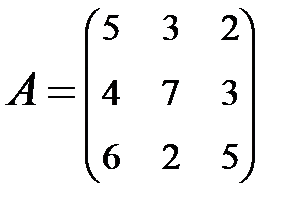 ;
; 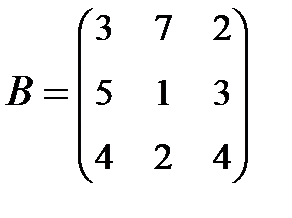 .
.
3. Найти А-1, где: 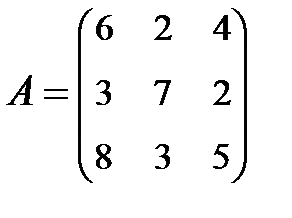 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ=  матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
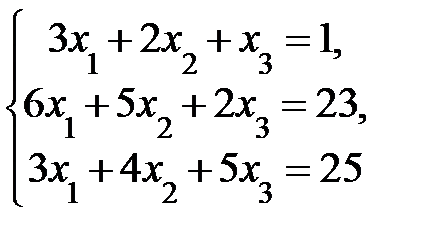 Сделать проверку.
Сделать проверку.
5. Даны уравнения двух медиан треугольника  и
и 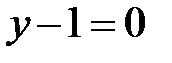 и одна из его вершин (1;3). Составить уравнения его сторон.
и одна из его вершин (1;3). Составить уравнения его сторон.
6. Даны координаты вершин пирамиды 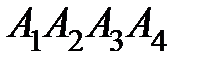 .
.
Найти: 1) длину ребра 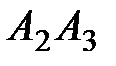 ; 2) угол между ребрами
; 2) угол между ребрами 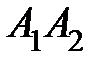 и
и 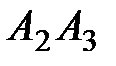 ; 3) угол между ребром
; 3) угол между ребром 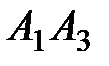 и гранью
и гранью  ; 4) площадь грани
; 4) площадь грани  ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
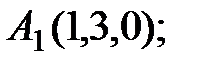
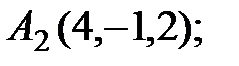
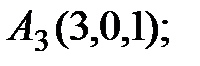

7. Найти точку К, симметричную точке М(1, 0, –1) относительно плоскости 2у+4z–1=0.
Варианты контрольной работы для студентов заочной формы обучения
Задача 1.
1.1. Граф, имеет матрицу инциденций  . Построить граф. Найти для него матрицу смежности.
. Построить граф. Найти для него матрицу смежности.
1.2. Граф, имеет матрицу смежности 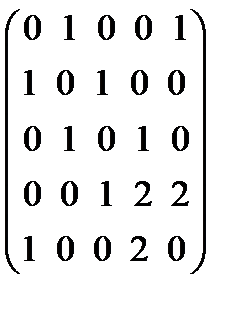 . Построить граф. Найти для него матрицу инциденций..
. Построить граф. Найти для него матрицу инциденций..
1.3. Граф, имеет матрицу инциденций  . Построить граф. Найти для него матрицу смежности.
. Построить граф. Найти для него матрицу смежности.
1.4. Граф, имеет матрицу смежности 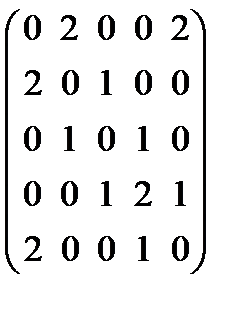 . Построить граф. Найти для него матрицу инциденций.
. Построить граф. Найти для него матрицу инциденций.
1.5. Граф, имеет матрицу инциденций 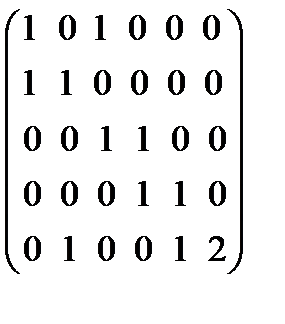 . Построить граф. Найти для него матрицу смежности.
. Построить граф. Найти для него матрицу смежности.
1.6. Граф, имеет матрицу смежности 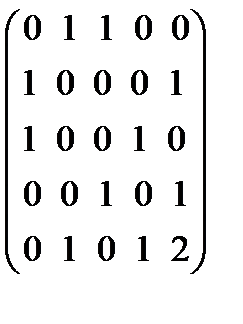 . Построить граф. Найти для него матрицу инциденций.
. Построить граф. Найти для него матрицу инциденций.
1.7. Граф, имеет матрицу инциденций  . Построить граф. Найти для него матрицу смежности.
. Построить граф. Найти для него матрицу смежности.
1.8. Граф, имеет матрицу смежности 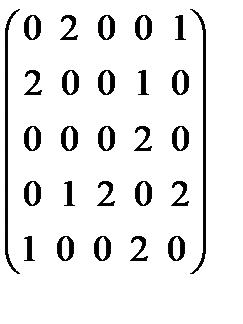 . Построить граф. Найти для него матрицу инциденций.
. Построить граф. Найти для него матрицу инциденций.
1.9. Граф, имеет матрицу инциденций  . Построить граф. Найти для него матрицу смежности.
. Построить граф. Найти для него матрицу смежности.
1.10. Граф, имеет матрицу смежности  . Построить граф. Найти для него матрицу инциденций.
. Построить граф. Найти для него матрицу инциденций.
Задача 2.
В пирамиде SABC: треугольник АВС – основание пирамиды, точка S – ее вершина. Даны координаты точек A, B, C, S.
2.1. А(-2;0;0); В(0;3;0); C(0;0;1); S(0;2;3).
2.2. А(4;0;0); В(0;-8;0); C(0;0;2); S(4;6;3).
2.3. А(-2;0;0); В(0;6;0); C(0;0;2); S(-1;6;4).
2.4. А(1;0;0); В(0;2;0); C(0;0;2); S(1;1;4).
2.5. А(-3;0;0); В(0;-2;0); C(0;0;1); S(-2;-1;3).
2.6. А(6;0;0); В(0;-3;0); C(0;0;2); S(4;-3;4).
2.7. А(3;0;0); В(0;-6;0); C(0;0;1); S(1;-3;3).
2.8. А(-4;0;0); В(0;4;0); C(0;0;2); S(-2;4;3).
2.9. А(-6;0;0); В(0;2;0); C(0;0;3); S(-3;2;5).
2.10. А(-1;0;0); В(0;5;0); C(0;0;2); S(-1;3;4).
Сделать чертеж. Найти:
1) длину ребра АВ;
2) угол между ребрами АВ и AS;
3) угол наклона ребра AS к основанию пирамиды;
4) площадь основания пирамиды;
5) объем пирамиды;
6) уравнение прямой АВ;
7) уравнение плоскости АВС;
8) проекцию вершины S на плоскость АВС;
9) длинувысоты пирамиды.
Задача 3.
Дана система линейных уравнений: 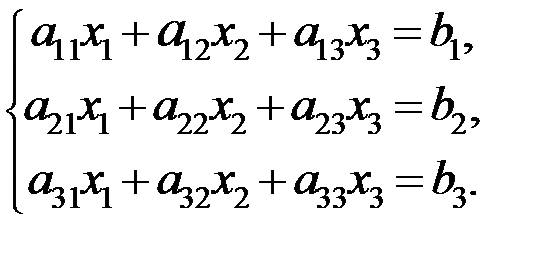
Доказать ее совместность и решить тремя способами: 1) методом Гаусса; 2) средствами матричного исчисления; 3) по правилу Крамера.
3.1. 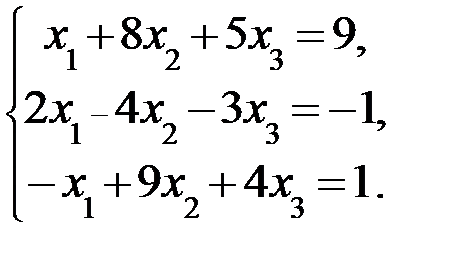 3.2.
3.2. 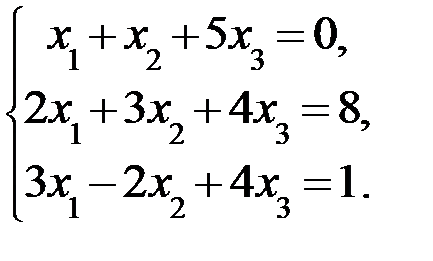
3.3. 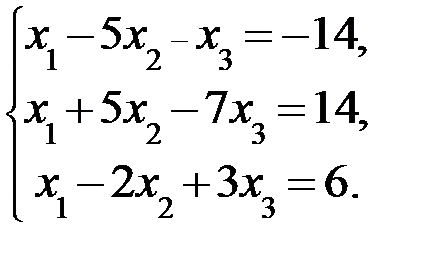 3.4.
3.4. 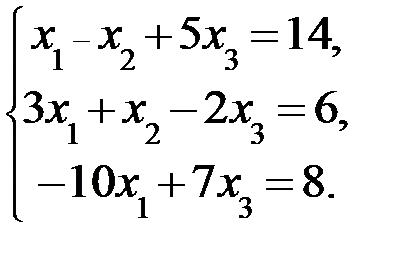
3.5. 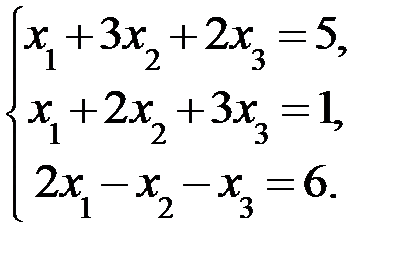 3.6.
3.6. 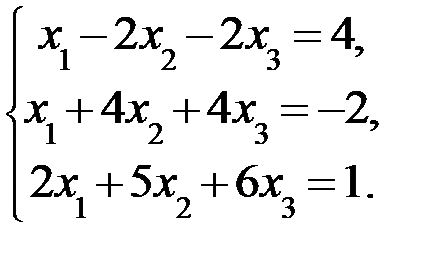
3.7.  3.8.
3.8. 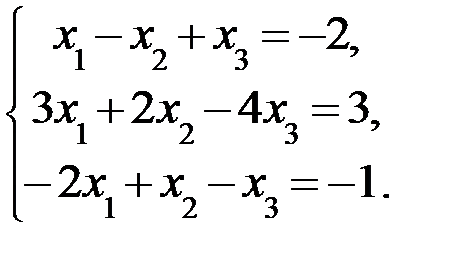
3.9. 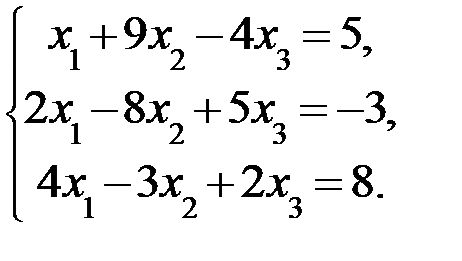 3.10.
3.10. 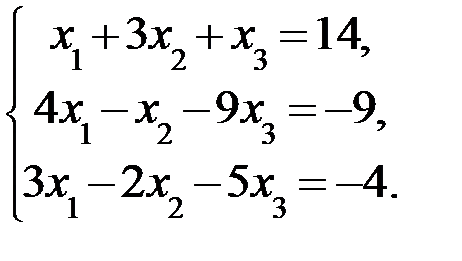
Задача 4.
Найти пределы функций, не пользуясь правилом Лопиталя.
4.1. а) 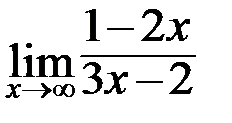 ; б)
; б)  ;
;
в) 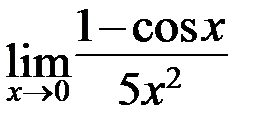 ; г)
; г)  .
.
4.2. а) 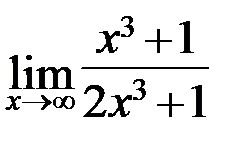 ; б)
; б) 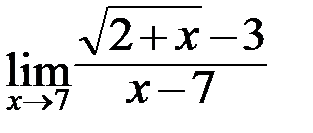 ;
;
в) 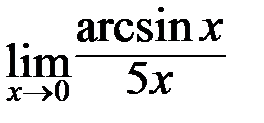 ; г)
; г) 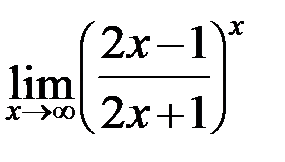 .
.
4.3. а) 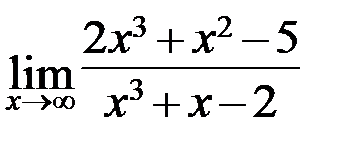 ; б)
; б)  ;
;
в)  ; г)
; г) 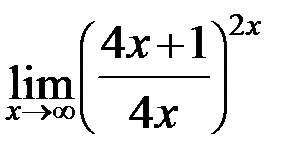 .
.
4.4. а) 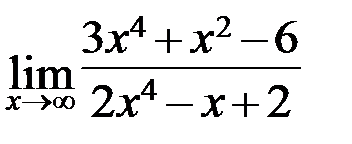 ; б)
; б) 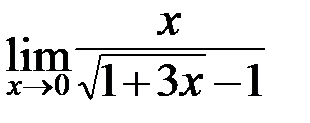 ;
;
в) 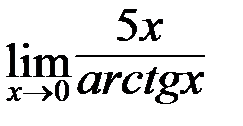 ; г)
; г) 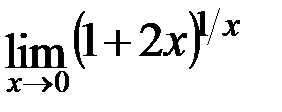 .
.
4.5. а) 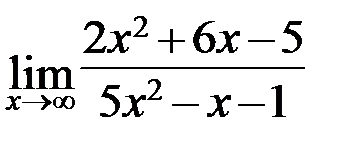 ; б)
; б) 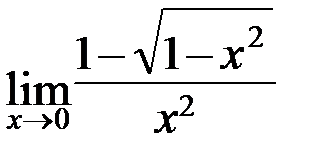 ;
;
в) 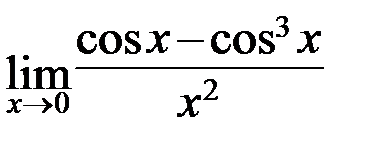 ; г)
; г)  .
.
4.6. а) 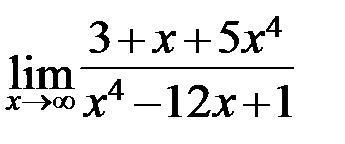 ; б)
; б) 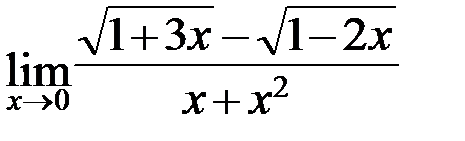 ;
;
в) 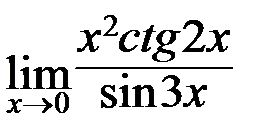 ; г)
; г) 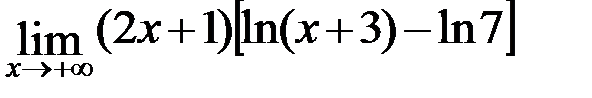 .
.
4.7. а) 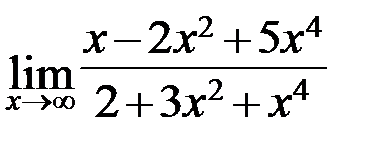 ; б)
; б) 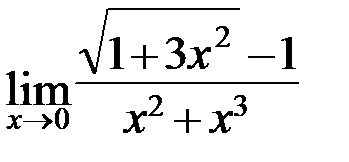 ;
;
в) 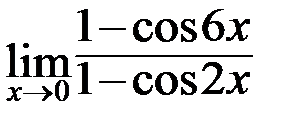 ; г)
; г) 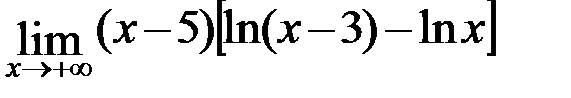 .
.
4.8. а)  ; б)
; б) 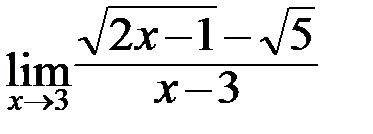 ;
;
в) 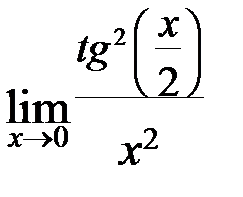 ; г)
; г)  .
.
4.9. а) 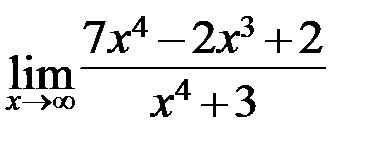 ; б)
; б)  ;
;
в) 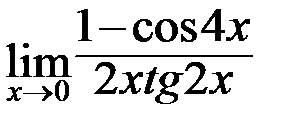 ; г)
; г) 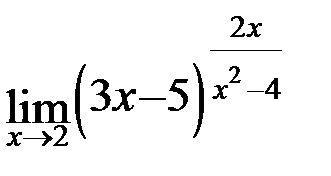 .
.
4.10. а) 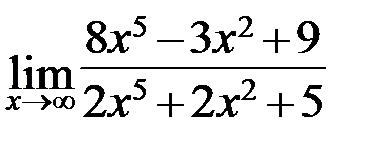 ; б)
; б)  ;
;
в) 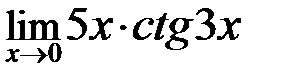 ; г)
; г) 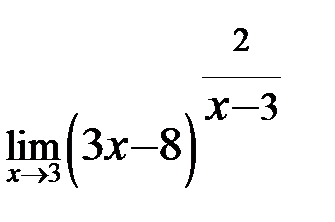 .
.
Задача 5.
Найти производные 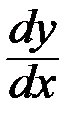 данных функций
данных функций
5.1. а) 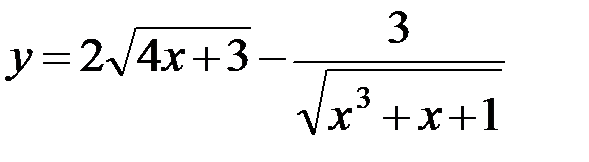 ; б)
; б)  ;
;
в) 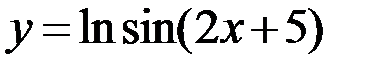 ; г)
; г) 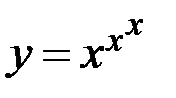 .
.
5.2. а) 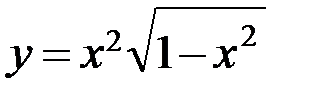 ; б)
; б) 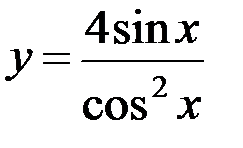 ; в)
; в) 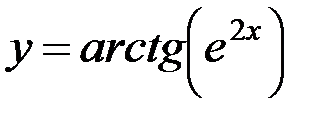 ;
;
г) 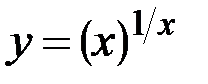 .
.
5.3. а)  ; б)
; б)  ; в)
; в)  ;
;
г)  .
.
5.4. а) 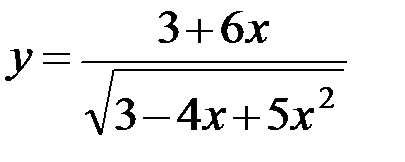 ; б)
; б) 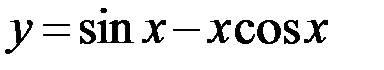 ;
;
в) 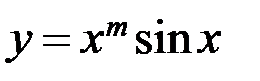 ; г)
; г)  .
.
5.5. а) 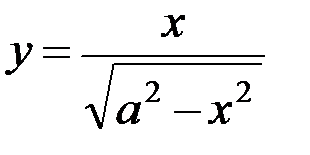 ; б)
; б) 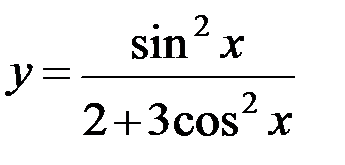 ; в)
; в) 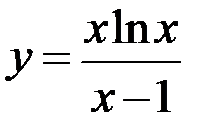 ;
;
г) 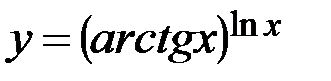 .
.
5.6. а) 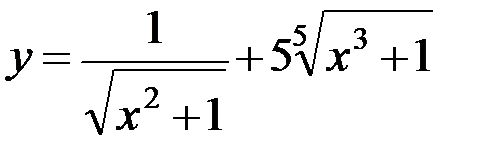 ; б)
; б) 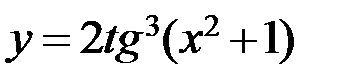 ;
;
в) 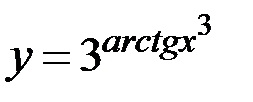 ; г)
; г) 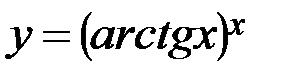 .
.
5.7. а) 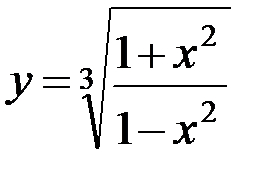 ; б)
; б) 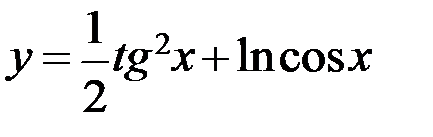 ;
;
в) 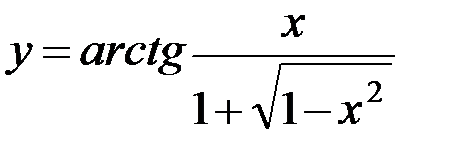 ; г)
; г) 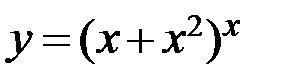 .
.
5.8. а) 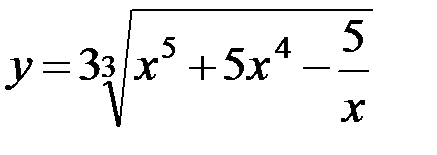 ; б)
; б) 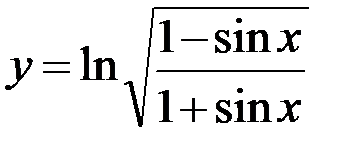 ;
;
в) 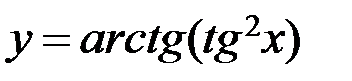 ; г)
; г) 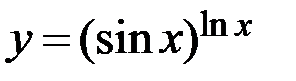 .
.
5.9. а) 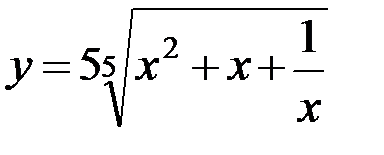 ; б)
; б) 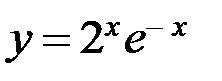 ; в)
; в) 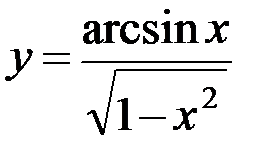 ;
;
г) 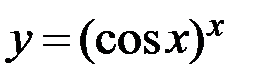 .
.
5.10. а) 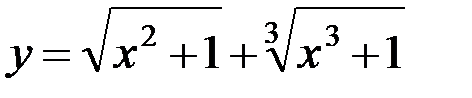 ; б)
; б) 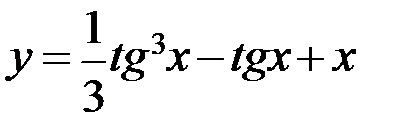 ;
;
в) 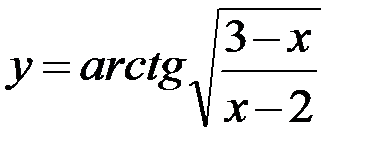 ; г)
; г) 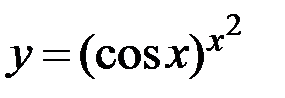 .
.
Задача 6.
Найти 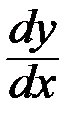 и
и 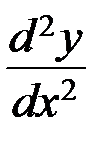 .
.
6.1. а) 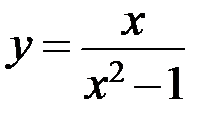 ; б)
; б) 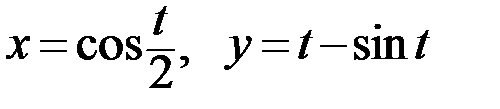 .
.
6.2. а) 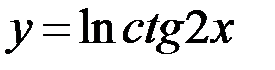 ; б)
; б) 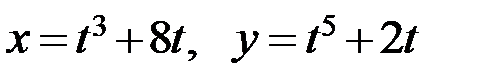 .
.
6.3. а)  ; б)
; б) 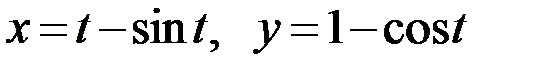 .
.
6.4. а) 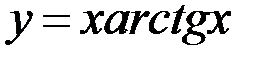 ; б)
; б) 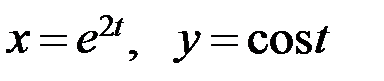 .
.
6.5. а)  ; б)
; б) 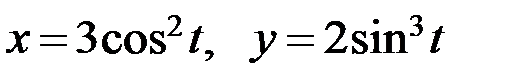 .
.
6.6. а) 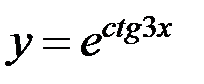 ; б)
; б)  .
.
6.7. а) 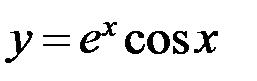 ; б)
; б) 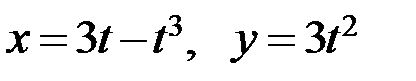 .
.
6.8. а) 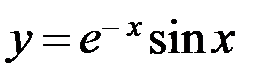 ; б)
; б)  .
.
6.9. а) 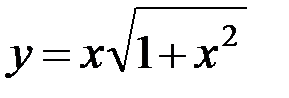 ; б)
; б)  .
.
6.10. а) 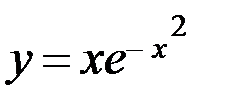 ; б)
; б) 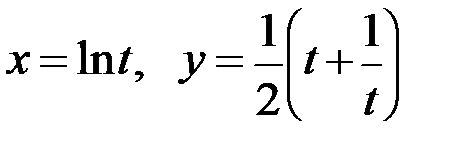 .
.
Задача 7.
Исследовать методами дифференциального исчисления функцию и, используя результаты исследования, построить ее график.
7.1. 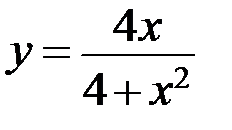 . 7.2.
. 7.2. 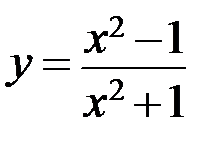 .
.
7.3. 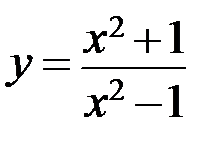 . 7.4.
. 7.4.  .
.
7.5.  . 7.6.
. 7.6. 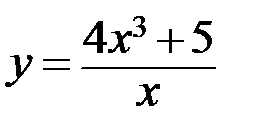 .
.
7.7. 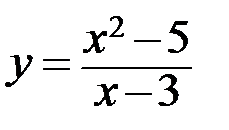 . 7.8.
. 7.8. 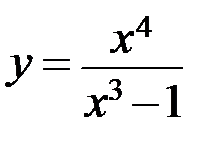 .
.
7.9. 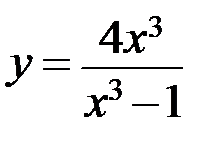 . 7.10.
. 7.10.  .
.
6.3. Вопросы для подготовки к зачету
1. Понятие высказывания. Операции над высказываниями и их свойства.
2. Понятие множества. Операции над множествами и их свойства.
3. Бинарные отношения. Свойства бинарных отношений.
4. Отношение эквивалентности. Его свойства.
5. Отношение порядка, Линейная упорядоченность.
6. Векторы в трехмерном пространстве, линейные операции над ними(сложение векторов и умножение вектора на число).
7. Основные свойства линейных операций над векторами.
8. Линейно зависимые и линейно независимые системы векторов. Базис и координаты вектора. Понятие об арифметических векторах.
9. Скалярное произведение векторов, его свойства, выражение в координатах. Выражение модуля вектора и угла между векторами через скалярное произведение векторов.
10. Ориентация тройки векторов. Векторное произведение векторов, его свойства и геометрический смысл. Условие коллинеарности векторов.
11. Смешанное произведение векторов, его свойства и геометрический смысл. Условие компланарности векторов.
12. Вычисление определителей квадратных матриц порядков n =1,2,3. Свойства определителей. Миноры и алгебраические дополнения.
13. Выражение векторного произведения двух векторов и смешанного произведения трех векторов в координатах.
14. Матрицы, линейные операции над ними. Операция умножения матриц.
15. Матрица, обратная данной.
16. Системы линейных алгебраических уравнений. Критерий совместности системы линейных алгебраических уравнений (теорема Кронекера-Капелли).
17. Различные методы решения систем n линейных уравнений с n неизвестными: матричный, Крамера, Гаусса.
18. Решение произвольной системы линейных алгебраических уравнений методом Гаусса. Базисные и свободные переменные.
19. Понятие линейного (векторного) пространства. Примеры.
20. Уравнения линий на плоскости. Различные формы уравнения прямой на плоскости.
21. Уравнения плоскости и прямой в пространстве. Угол между плоскостями. Угол между прямыми. Угол между прямой и плоскостью.
22. Кривые второго порядка: окружность, эллипс, гипербола, парабола, их геометрические свойства, уравнения и формы.
23. Понятие функции одной переменной. Способы задания функций. Область определения и область значений функции, ее график. Свойства функции: симметрия, ограниченность, монотонность.
24. Убывающие и возрастающие функции. Сложная и обратная функции.
25. Основные элементарные функции, их свойства и графики.
26. Предел функции в точке. Основные теоремы о пределах функций.
27. Непрерывность функции на промежутке. Основные теоремы о свойствах непрерывных функций.
28. Классификация точек разрыва функций.
29. Бесконечно малые и бесконечно большие функции, свойства бесконечно малых функций.Сравнение бесконечно малых функций.
30. Виды неопределенностей и способы их раскрытия. Первый замечательный предел. Второй замечательный предел.
31. Производная функции, ее геометрический и механический смысл. Дифференцируемость функции в точке. Дифференциал функции.
32. Основные свойства производных (правила дифференцирования). Производная сложной и обратной функций. Таблица производных для основных элементарных функций.
33. Производные и дифференциалы высших порядков.
34. Теорема Лагранжа о конечных приращениях.
35. Правило Лопиталя.
36. Формула Тейлора с остаточным членом форме Лагранжа.
37. Условия монотонности функции. Экстремумы функции, необходимое условие. Достаточные условия.
38. Отыскание наибольшего и наименьшего значений функции дифференцируемой на отрезке.
39. Исследование выпуклости функций. Точки перегиба.
40. Асимптоты функций.
41. Общая схема исследования свойств функции и построения ее графика.
7. УЧЕБНО-МЕТОДИЧЕСКОЕ И ИНФОРМАЦИОННОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
Литература
Основная литература
1. Кузнецов Л. А. Сборник заданий по высшей математике. Типовые расчеты [Электронный ресурс] : учеб.пособие для вузов [Гриф Минобразования РФ] / Л. А. Кузнецов. - 11-е изд., стер. - Санкт-Петербург: Лань, 2015. - 240 с. - Режим доступа: http://e.lanbook.com/view/book/219/.
2. Назаров А. И. Курс математики для нематематических специальностей и направлений бакалавриата [Электронный ресурс]: учеб.пособие для вузов [Гриф УМО] / А. И. Назаров, И. А. Назаров. - СПБ.: Лань, 2011. - 576 с.: ил. - Режим доступа: http://e.lanbook.com/view/book/1797/.
3. Перминов Е. А. Дискретная математика: авторское учебное пособие. Екатеринбург: [Электронный ресурс], 2015. 156 с. Режим доступа: http://umkd.rsvpu.ru/download/10059?type=pdf
4. Шипачев В. С. Высшая математика. Базовый курс: учебник и практикум для бакалавров [Гриф Минобразования РФ] / В. С. Шипачев; под ред. А. Н. Тихонова. - 8-е изд., перераб. и доп. - Москва :Юрайт, 2015. - 447 с.
5. Шипачев В. С. Высшая математика: учебник и практикум для бакалавров [Гриф Минобрнауки РФ] / В. С. Шипачев ; под ред. А. Н. Тихонова ; Моск. гос. ун-т им. М. В. Ломоносова. - 8-е изд., перераб. и доп. - Москва: Юрайт, 2015. - 447 с.
Дополнительная литература
6. Высшая математика в упражнениях и задачах [Текст]: учебное пособие для вузов. В 2 ч. Ч. 1 / П. Е. Данко [и др.]. – М.: Оникс: Мир и Образование, 2008. – 368 с.
7. Высшая математика в упражнениях и задачах[Текст]: учебное пособие для вузов. В 2 ч. Ч. 2 / П. Е. Данко [и др.]. – М.: Оникс : Мир и Образование, 2009. - 448 с.
8. Письменный Д.Т. Конспект лекций по высшей математике [Текст]: полный курс: [учебное пособие для вузов] / Письменный Д. Т . –М.: Айрис-пресс, 2011. – 602 с.
Дата: 2018-11-18, просмотров: 358.