Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Алгоритм – строгая последовательность действий, описывающая процесс преобразования объекта из начального состояния в конечное, записанная с помощью понятных исполнителю команд.

Исполнитель – это объект, выполняющий действия.

Алгоритмизация — процесс разработки алгоритма (плана действий) для решения задачи.

Алгоритмы состоят из отдельных команд, которые выполняются одна за другой в определённой последовательности.

Виды алгоритмов:

· Линейный;

· Циклический;

· Разветвляющийся.

Линейным называется такой алгоритм, при котором все действия выполняются однократно в заданном порядке.

Циклический алгоритм – это алгоритм, в котором все действия должны повторяться указанное число раз или пока не выполнено заданное условие.

Разветвляющийся алгоритм – это алгоритм, в котором в зависимости от условия выполняется либо одна, либо другая последовательность действий.

Свойства алгоритмов:

1.

12

Дискретность (от латинского разделённый, прерывистый) – позволяет разделять информационный процесс в алгоритме на отдельные команды;

2. Детерминированность (от латинского определённость, точность) – это ясность для исполнителя последовательности выполнения команд;

3. Результативность – это свойство, обеспечивающее преобразование объекта из начального состояния в конечное за конечное число шагов;

4. Массовость – это свойство предполагает, что алгоритм должен быть пригоден для решения всех задач данного типа;

5. Конечность - каждое действие в отдельности и алгоритм в целом должны иметь возможность завершения.

Алгоритм должен быть формализован по некоторым правилам посредством конкретных изобразительных средств. К ним относятся следующие способы записи алгоритмов: словесный, формульно-словесный, графический, язык операторных схем, алгоритмический язык.

Наибольшее распространение благодаря своей наглядности получил графический (в виде блок-схем) способ записи алгоритмов.

Блок-схемой называется графическое изображение логической структуры алгоритма, в котором каждый этап процесса обработки информации представляется в виде геометрических символов (блоков), имеющих определенную конфигурацию в зависимости от характера выполняемых операций.

 

	13

Изображение элементов алгоритма:

Начало (конец) алгоритма;

Команда алгоритма;

 

Условие алгоритма (это высказывание, которое может быть либо истинным, либо ложным);

 

Ввод (вывод) данных.

 

Циклическая частота

	14

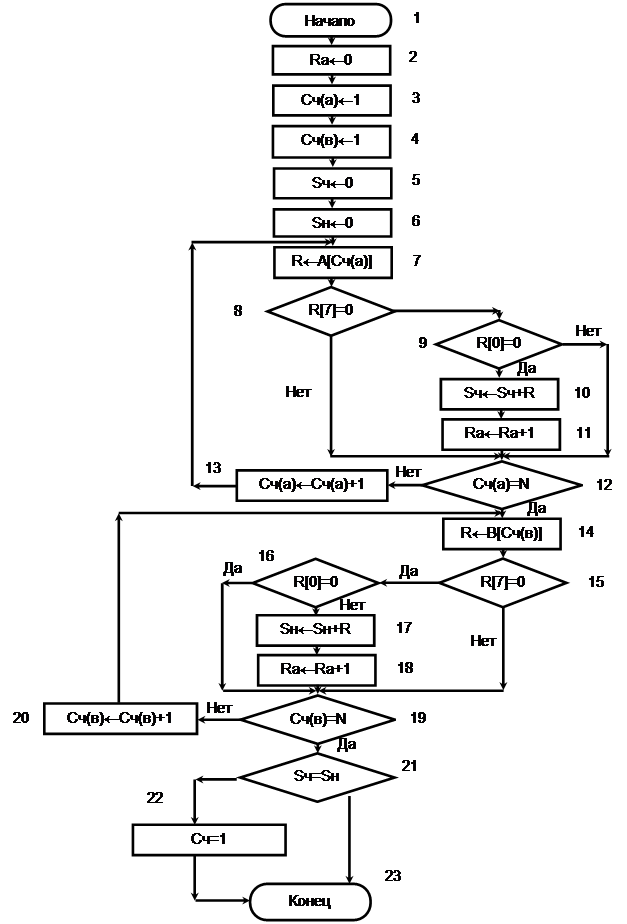4.2  Схема алгоритма

 

 

	15

Описание алгоритма

1. Начало;

2. Обнуляем регистр адреса Rа: Rа0;

3. Записываем в счётчик Сч(а) число 1: Сч(а)1;

4. Записываем в счётчик Сч(в) число 1: Сч(в)1;

5. Записываем в регистр сумму чётных чисел Sч: число 0: Sч0;

6. Записываем в регистр сумму нечётных чисел Sн: число 0: Sн0;

7. Считываем в регистр R число из массива А с порядковым номером Сч(а) (с тем числом, которое хранится в этом счётчике): RА[Сч(а)];

8. Проверяем число на «знак»: R[7]=0. Если старший разряд числа:

· равен 0, то число положительное, переходим к шагу 9;

· не равен 0, то число отрицательное, переходим к шагу 12;

9. Проверяем число на чётность: R[0]=0. Если младший разряд числа:

· равен 0, то число чётное, переходим к шагу 10;

· не равен 0, то число нечётное, переходим к шагу 12;

10. Производим сложение числа, находящегося в регистре Sч и числа, находящегося в регистре R. Результат помещаем в регистр Sч: SчSч+R;

11. Увеличиваем адрес числа на 1: RаRа+1;

12. Проверяем, последнее ли это число массива А: Сч(а)=N:

· если да, то переходим к шагу 14;

· если нет, то переходим к шагу 13;

13. Увеличиваем значение счётчика Сч(а) на единицу: Сч(а)Сч(а)+1 и переходим к шагу 7;

14. Считываем в регистр R число из массива В с порядковым номером Сч(в): RВ[Сч(в)];

15. Проверяем число на «знак»: R[7]=0. Если старший разряд числа:

· равен 0, то число положительное, переходим к шагу 16;

·

16

не равен 0, то число отрицательное, переходим к шагу 19;

16. Проверяем число на чётность: R[0]=0. Если младший разряд числа:

· равен 0, то число чётное, переходим к шагу 19;

· не равен 0, то число нечётное, переходим к шагу 17;

17. Производим сложение числа, находящегося в регистре Sн и числа, находящегося в регистре R. Результат помещаем в регистр Sн: SнSн+R;

18. Увеличиваем адрес числа на 1: RаRа+1;

19. Проверяем, последнее ли это число массива В: Сч(в)=N:

· если да, то переходим к шагу 21;

· если нет, то переходим к шагу 20;

20. Увеличиваем значение счётчика Сч(в) на единицу: Сч(в)Сч(в)+1 и переходим к шагу 14;

21. Сравниваем сумму чётных и нечётных чисел: Sч=Sн;

· Если да, то переходим к шагу 22;

· Если нет, то переходим к шагу 23;

22. Сч=1;

23. Конец.

 

 

	17