В экономических исследования редко приходится иметь дело с точными и определенными функциональными связями, когда каждому значению одной величины соответствует строго определённое значение другой величины. Чаще встречаются стохастические (вероятностные) или корреляционные связи. В следующем разделе работы с помощью программы Excel проводится исследование корреляционной связи.
При изучении корреляционных связей возникает необходимость решить две основные задачи – о тесноте и о форме связи. Первая решается методом корреляции, вторая – методом регрессии и дисперсии. По форме корреляционная связь может быть линейной и нелинейной, по направлению – прямой и обратной.
Для анализа линейной корреляции между признаками Х и Y проводят n независимых парных наблюдений , исходом каждого из которых является пара чисел ( X1,Y1), ( X2,Y2),… ( X n,Yn). По этим значениям определяют выборочные эмпирические коэффициенты корреляции и регрессии, рассчитывают уравнение регрессии, строят теоретическую линию регрессии и оценивают значимость полученных результатов.
В MS Excel линия уравнения регрессии называется линией тренда, которая показывает тенденцию изменения данных и служит для составления прогнозов. Для создания линии тренда на основе диаграммы используется один из пяти типов аппроксимаций или линейная фильтрация.
 |
Тип Описание
 |
Линейная y = m*x+ b
где m – тангенс угла наклона,
b – точка пересечения с осью ординат
Логарифмическая y = c*ln(х) + b
где c и b – константы
Полиномиальная y = c6 x6 +…+ c1x+b
где c6,… c1 и b – константы
Степенная y = c*xb
где c и b – константы
Экспоненциальная y = c*ebx
где c и b – константы
На диаграмме можно выделить любой ряд данных и добавить к нему линию тренда. Когда линия тренда добавляется к ряду данных, она связывается с ним, и поэтому при изменении значений любых точек ряда данных линия тренда автоматически пересчитывается и обновляется на диаграмме.
Кроме того, имеется возможность выбирать точку, в которой линия тренда пересекает ось ординат, добавлять к диаграмме уравнение регрессии и величину достоверности аппроксимации. Покажем построение линии тренда на нашем демонстрационном примере на основе исходных данных: время уборки и урожайность. Данный анализ проводится на основе диаграммы для пяти типов аппроксимаций, и выбираем ту линию тренда, для которой величина достоверности аппроксимации наибольшая, т.е. у которой самый наибольший коэффициент корреляции.
Квадрат коэффициента корреляции равен 0,8572. Уравнение данной зависимости имеет вид:
Ух = 58,964х2-88,707х+112,8
Для оценки степени пригодности полученного корреляционного уравнения в практических целях необходимо проверить его достоверность.
Рассчитываем ошибку уравнения по формуле:
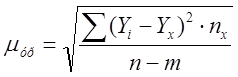
где Yi - фактическое значение результативного признака, в демонстрационном примере – это Уфакт.; Yх - значения результативного признака, рассчитанные по уравнению регрессии, в демонстрационном примере – это Урасчетн.; n –число наблюдений, m- число параметров уравнения регрессии.
Значения Yх рассчитываются по уравнению регрессии путем подставления в него значений фактического признака (х). В РГР необходимо подсчитать ошибку уравнения для всех видов зависимостей, найти относительную ошибку уравнения, а также выявить минимальную ошибку уравнения регрессии, и убедиться, что она соответствует той зависимости, у которой самый высокий коэффициент аппроксимации (R2).
Минимальная ошибка уравнения равна 5,308431. Она соответствует линейной зависимости, у которой самый высокий коэффициент аппроксимации (R2), равный 0,8572.
Дата: 2019-12-22, просмотров: 308.