САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ
АГРАРНЫЙ УНИВЕРСИТЕТ
ИМ. Н.И. В АВИЛОВА
КАФЕДРА ЭКОНОМИЧЕСКОЙ КИБЕРНЕТИКИ
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА
ПО МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ
Выполнила студент III курса группы Б-303
Хуртов Денис
Саратов 2009 г.
Таблица исходных данных.
Вариант № 46
| № хозяйства | Расход кормов, и.к.ед. (Х) | Себестоимость 1 ц. молока, руб. (У) |
| 1 | 1,27 | 95,6 |
| 2 | 1,92 | 148,8 |
| 3 | 1,63 | 115,7 |
| 4 | 1,54 | 115,7 |
| 5 | 1,49 | 110,5 |
| 6 | 1,62 | 121,9 |
| 7 | 1,48 | 110,9 |
| 8 | 1,19 | 91,5 |
| 9 | 1,53 | 110,5 |
| 10 | 1,33 | 91,5 |
| 11 | 1,60 | 121,9 |
| 12 | 1,43 | 110,5 |
| 13 | 1,45 | 110,5 |
| 14 | 1,63 | 110,5 |
| 15 | 1,71 | 148,8 |
| 16 | 1,23 | 91,5 |
| 17 | 1,27 | 95,6 |
| 18 | 1,43 | 110,5 |
| 19 | 1,07 | 85,0 |
| 20 | 1,21 | 91,5 |
| 21 | 1,61 | 121,9 |
| 22 | 1,58 | 115,7 |
| 23 | 1,57 | 110,5 |
| 24 | 1,43 | 110,5 |
| 25 | 1,45 | 115,7 |
| 26 | 1,43 | 95,6 |
| 27 | 1,74 | 148,8 |
| 28 | 1,53 | 110,5 |
| 29 | 1,54 | 115,7 |
| 30 | 1,76 | 148,8 |
Х – независимый признак;
У – зависимый признак.
Оглавление
Введение…………………………………………………………………………...4
Глава 1. Построение и графическое изображение вариационных рядов.
1.1 Порядок построения вариационных рядов………………………………….5
1.2. Графическое изображение дискретных вариационных рядов……………6
1.3. Графическое изображение интервальных вариационных рядов………….6
Глава 2. Статистические характеристики рядов распределения.
2.1. Показатели центра распределения……………………………………….….7
2.2. Показатели колеблемости признака……………………………………….8
2.3. Показатели формы распределения……………………………..…………..9
2.4. Построение нормальной кривой по эмпирическим и теоретическим данным……………………………………………………………………………10
2.5. Проверка гипотезы о законе нормального распределения……………….11
2.6. Проверка гипотезы о законе нормального распределения по критерию Пирсона с помощью табличного процессора Excel………………………...…11
2.7. Статистические оценки параметров распределения…………………...…13
2.8. Статистические оценки параметров распределения……………………...14
Глава 3. Корреляционно – регрессионный анализ.
3.1. Выбор типа аппроксимирующей функции…………………………….….16
3.2. Исследование корреляционной связи и оценка степени пригодности полученного корреляционного уравнения……………………………………..18
3.3. Вычисление показателей тесноты корреляционной связи……………….19
3.4. Проведение регрессионного анализа с помощью инструмента
Регрессия ………………………………………………………………………...19
Глава 4. Дисперсионный анализ.
4.1. Понятие дисперсионного анализа……………………………………….…20
4.2. Однофакторный дисперсионный анализ…………………………………..20
Список литературы……………………………………………………………....21
Приложения……………………………………………………………………...22
Введение
Расчетно-графическая работа (РГР) предполагает применение основных приемов статистики для обработки массовой социально – экономической информации.
Программное обеспечение современных персональных компьютеров позволяет автоматизировать процесс расчетов. Наиболее эффективно использовать для этой цели табличный процессор Excel.
Excel предлагает широкий диапазон средств для анализа статистических данных. Такие встроенные функции, как СРЗНАЧ, МЕДИАНА, МОДА, могут быть полезны для проведения несложного анализа. Если встроенных статистических функций недостаточно, то можно обратиться к Пакету анализа.
Пакет анализа, являющийся надстройкой, содержит коллекцию функций и инструментов, расширяющих встроенные аналитические возможности Excel. В частности, пакет анализа можно использовать для создания гистограмм, ранжирования данных, извлечения случайных или периодических выборок из выбора данных, проведения регрессионного анализа, получения основных статистических характеристик выборки, генерации случайных чисел с различным распределением и для многих других расчетов.
Глава 1. Построение и графическое изображение
Вариационных рядов.
Глава 3. Корреляционно – регрессионный анализ.
Глава 4. Дисперсионный анализ.
Список литературы
1. Венецкий И.Г., Кильдишев В.С. Теория вероятностей и математическая статистика. М.: Статистика, 1975.
2. Ефимова М.Р., Рябцев В.М. Общая теория статистики. М.: Финансы и статистика, 1991.
3. Марк Джон, Крейг Стинсон. Эффективная работа с Microsoft Excel 2000. СПб.: Питер 2001.
4. Блаттнер Патрик. Использование Microsoft Excel 2002. М.: Издательский дом «Вильямс», 2002.
Приложение 1.
Значение дифференциальной функции Лапласа
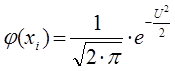
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0,0 | 0,3989 | ,3989 | ,3989 | ,3988 | ,3986 | ,3984 | ,3982 | ,3980 | ,3977 | ,3973 |
| 0,1 | ,3970 | ,3965 | ,3961 | ,3956 | ,3951 | ,3945 | ,3939 | ,3932 | ,3925 | ,3918 |
| 0,2 | ,3910 | ,3902 | ,3894 | ,3885 | ,3846 | ,3857 | ,3857 | ,3847 | ,3836 | ,3825 |
| 0,3 | ,3814 | ,3802 | ,3790 | ,3778 | ,3765 | ,3752 | ,3739 | ,3726 | ,3712 | ,3697 |
| 0,4 | ,3683 | ,3668 | ,3652 | ,3637 | ,3621 | ,3605 | ,3589 | ,3572 | ,3555 | ,3538 |
| 0,5 | ,3521 | ,3503 | ,3485 | ,3467 | ,3448 | ,3429 | ,3410 | ,3391 | ,3372 | ,3352 |
| 0,6 | ,3332 | ,3312 | ,3292 | ,3271 | ,3251 | ,3230 | ,3209 | ,3187 | ,3166 | ,3134 |
| 0,7 | ,3123 | ,3101 | ,3079 | ,3056 | ,3054 | ,3011 | ,2989 | ,2966 | ,2973 | ,2920 |
| 0,8 | ,2897 | ,2874 | ,2850 | ,2827 | ,2803 | ,2780 | ,2756 | ,2732 | ,2709 | ,2685 |
| 0,9 | ,2661 | ,2637 | ,2613 | ,2589 | ,2565 | ,2541 | ,2516 | ,2492 | ,2468 | ,2443 |
| 1,0 | ,2420 | ,2396 | ,2371 | ,2347 | ,2323 | ,2299 | ,2275 | ,2251 | ,2227 | ,2203 |
| 1,1 | ,2179 | ,2155 | ,2131 | ,2107 | ,2083 | ,2059 | ,2036 | ,2012 | ,1989 | ,1965 |
| 1,2 | ,1942 | ,1919 | ,1895 | ,1872 | ,1849 | ,1826 | ,1804 | ,1781 | ,1758 | ,1736 |
| 1,3 | ,1714 | ,1691 | ,1696 | ,1647 | ,1626 | ,1604 | ,1582 | ,1561 | ,1539 | ,1518 |
| 1,4 | ,1497 | ,1476 | ,1456 | ,1435 | ,1415 | ,1394 | ,1374 | ,1354 | ,1334 | ,1315 |
| 1,5 | ,1295 | ,1276 | ,1267 | ,1238 | ,1219 | ,1200 | ,1182 | ,1163 | ,1145 | ,1127 |
| 1,6 | ,1109 | ,1092 | ,1074 | ,1057 | ,1040 | ,1023 | ,1006 | ,0989 | ,0973 | ,0957 |
| 1,7 | ,0940 | ,0925 | ,0909 | ,0893 | ,0878 | ,0863 | ,0848 | ,0843 | ,0818 | ,0804 |
| 1,8 | ,0790 | ,0775 | ,0761 | ,0748 | ,0734 | ,0721 | ,0707 | ,0694 | ,0681 | ,0669 |
| 1,9 | ,0658 | ,0644 | ,0632 | ,0620 | ,0608 | ,0596 | ,0584 | ,0573 | ,0562 | ,0551 |
| 2,0 | ,0540 | ,0529 | ,0519 | ,0508 | ,0498 | ,0488 | ,0478 | ,0468 | ,0459 | ,0449 |
| 2,1 | ,0440 | ,0431 | ,0422 | ,0413 | ,0404 | ,0396 | ,0387 | ,0379 | ,0371 | ,0363 |
| 2,2 | ,0355 | ,0347 | ,0339 | ,0332 | ,0325 | ,0317 | ,0310 | ,0303 | ,0227 | ,0290 |
| 2,3 | ,0283 | ,0277 | ,0270 | ,0264 | ,0258 | ,0252 | ,0246 | ,0241 | ,0235 | ,0229 |
| 2,4 | ,0224 | ,0219 | ,0213 | ,0208 | ,0203 | ,0198 | ,0194 | ,0189 | ,0184 | ,0180 |
| 2,5 | ,0173 | ,0171 | ,0167 | ,0163 | ,0158 | ,0154 | ,0151 | ,0147 | ,0143 | ,0139 |
| 2,6 | ,0136 | ,0132 | ,0129 | ,0126 | ,0122 | ,,0119 | ,0116 | ,0113 | ,0110 | ,0107 |
| 2,7 | ,0104 | ,0101 | ,0098 | ,0096 | ,0093 | ,0091 | ,0088 | ,0086 | ,0084 | ,0081 |
| 2,8 | ,0079 | ,0077 | ,0075 | ,0073 | ,0071 | ,0069 | ,0067 | ,0065 | ,0063 | ,0061 |
| 2,9 | ,0060 | ,0058 | ,0056 | ,0055 | ,0053 | ,0051 | ,0050 | ,0048 | ,0047 | ,0046 |
| 3,0 | ,0044 | ,0043 | ,0042 | ,0040 | ,0039 | ,0038 | ,0037 | ,0036 | ,0035 | ,0034 |
| 3,1 | ,0033 | ,0032 | ,0031 | ,0030 | ,0029 | ,0028 | ,0027 | ,0026 | ,0025 | ,0025 |
| 3,2 | ,0024 | ,0023 | ,0022 | ,0022 | ,0021 | ,0020 | ,0020 | ,0019 | ,0018 | ,0018 |
| 3,3 | ,0017 | ,0017 | ,0016 | ,0016 | ,0015 | ,0015 | ,0014 | ,0014 | ,0013 | ,0013 |
| 3,4 | ,0012 | ,0012 | ,0012 | ,0011 | ,0011 | ,0010 | ,0010 | ,0010 | ,0009 | ,0009 |
| 3,5 | ,0009 | ,0008 | ,0008 | ,0008 | ,0008 | ,0007 | ,0007 | ,0007 | ,0007 | ,0006 |
| 3,6 | ,0006 | ,0006 | ,0006 | ,0005 | ,0005 | ,0005 | ,0005 | ,0005 | ,0005 | ,0004 |
| 3,7 | ,0004 | ,0004 | ,0004 | ,0004 | ,0004 | ,0004 | ,0003 | ,0003 | ,0003 | ,0003 |
| 3,8 | ,0003 | ,0003 | ,0003 | ,0003 | ,0003 | ,0002 | ,0002 | ,0002 | ,0002 | ,0002 |
| 3,9 | ,0002 | ,0002 | ,0002 | ,0002 | ,0002 | ,0002 | ,0002 | ,0002 | ,0001 | ,0001 |
Приложение 2.
Критические точки распределения x 2
| Уровень Значимости, α | Число степеней свободы, к | ||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| 0,01 | 6,6 | 9,2 | 11,3 | 13,3 | 15,1 | 16,8 | 18,5 | 20,1 | 21,7 | 23,2 | 24,7 | 26,2 | 27,7 | 29,1 | 30,6 |
| 0,05 | 3,8 | 6,0 | 7,8 | 9,9 | 11,1 | 12,6 | 14,1 | 15,5 | 16,9 | 18,3 | 19,7 | 21,0 | 22,4 | 23,7 | 25,0 |
Приложение 3.
Критические точки распределения Стьюдента
| Число степеней свободы, к | Уровень значимости, α (двусторонняя критическая область) | Число степеней свободы к | Уровень значимости, α (двусторонняя критическая область) | ||
| 0,05 | 0,01 | 0,05 | 0,01 | ||
| 1 | 12,7 | 63,7 | 18 | 2,10 | 2,88 |
| 2 | 4,30 | 9,92 | 19 | 2,09 | 2,86 |
| 3 | 3,18 | 5,84 | 20 | 2,09 | 2,85 |
| 4 | 2,78 | 4,60 | 21 | 2,08 | 2,83 |
| 5 | 2,57 | 4,03 | 22 | 2,07 | 2,82 |
| 6 | 2,45 | 3,71 | 23 | 2,07 | 2,81 |
| 7 | 2,36 | 3,50 | 24 | 2,06 | 2,80 |
| 8 | 2,31 | 3,36 | 25 | 2,06 | 2,79 |
| 9 | 2,26 | 3,25 | 26 | 2,06 | 2,78 |
| 10 | 2,23 | 3,17 | 27 | 2,05 | 2,77 |
| 11 | 2,20 | 3,11 | 28 | 2,05 | 2,76 |
| 12 | 2,18 | 3,05 | 29 | 2,05 | 2,76 |
| 13 | 2,16 | 3,01 | 30 | 2,04 | 2,75 |
| 14 | 2,14 | 2,98 | 40 | 2,02 | 2,70 |
| 15 | 2,13 | 2,95 | 60 | 2,00 | 2,66 |
| 16 | 2,12 | 2,92 | 120 | 1,98 | 2,62 |
| 17 | 2,11 | 2,90 | - | 1,96 | 2,58 |
|
| 2,025 | 0,005 | |||
| Уровень значимости α (односторонняя критическая область) | |||||
САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ
АГРАРНЫЙ УНИВЕРСИТЕТ
ИМ. Н.И. В АВИЛОВА
КАФЕДРА ЭКОНОМИЧЕСКОЙ КИБЕРНЕТИКИ
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА
ПО МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ
Выполнила студент III курса группы Б-303
Хуртов Денис
Саратов 2009 г.
Таблица исходных данных.
Вариант № 46
| № хозяйства | Расход кормов, и.к.ед. (Х) | Себестоимость 1 ц. молока, руб. (У) |
| 1 | 1,27 | 95,6 |
| 2 | 1,92 | 148,8 |
| 3 | 1,63 | 115,7 |
| 4 | 1,54 | 115,7 |
| 5 | 1,49 | 110,5 |
| 6 | 1,62 | 121,9 |
| 7 | 1,48 | 110,9 |
| 8 | 1,19 | 91,5 |
| 9 | 1,53 | 110,5 |
| 10 | 1,33 | 91,5 |
| 11 | 1,60 | 121,9 |
| 12 | 1,43 | 110,5 |
| 13 | 1,45 | 110,5 |
| 14 | 1,63 | 110,5 |
| 15 | 1,71 | 148,8 |
| 16 | 1,23 | 91,5 |
| 17 | 1,27 | 95,6 |
| 18 | 1,43 | 110,5 |
| 19 | 1,07 | 85,0 |
| 20 | 1,21 | 91,5 |
| 21 | 1,61 | 121,9 |
| 22 | 1,58 | 115,7 |
| 23 | 1,57 | 110,5 |
| 24 | 1,43 | 110,5 |
| 25 | 1,45 | 115,7 |
| 26 | 1,43 | 95,6 |
| 27 | 1,74 | 148,8 |
| 28 | 1,53 | 110,5 |
| 29 | 1,54 | 115,7 |
| 30 | 1,76 | 148,8 |
Х – независимый признак;
У – зависимый признак.
Оглавление
Введение…………………………………………………………………………...4
Глава 1. Построение и графическое изображение вариационных рядов.
1.1 Порядок построения вариационных рядов………………………………….5
1.2. Графическое изображение дискретных вариационных рядов……………6
1.3. Графическое изображение интервальных вариационных рядов………….6
Глава 2. Статистические характеристики рядов распределения.
2.1. Показатели центра распределения……………………………………….….7
2.2. Показатели колеблемости признака……………………………………….8
2.3. Показатели формы распределения……………………………..…………..9
2.4. Построение нормальной кривой по эмпирическим и теоретическим данным……………………………………………………………………………10
2.5. Проверка гипотезы о законе нормального распределения……………….11
2.6. Проверка гипотезы о законе нормального распределения по критерию Пирсона с помощью табличного процессора Excel………………………...…11
2.7. Статистические оценки параметров распределения…………………...…13
2.8. Статистические оценки параметров распределения……………………...14
Глава 3. Корреляционно – регрессионный анализ.
3.1. Выбор типа аппроксимирующей функции…………………………….….16
3.2. Исследование корреляционной связи и оценка степени пригодности полученного корреляционного уравнения……………………………………..18
3.3. Вычисление показателей тесноты корреляционной связи……………….19
3.4. Проведение регрессионного анализа с помощью инструмента
Регрессия ………………………………………………………………………...19
Глава 4. Дисперсионный анализ.
4.1. Понятие дисперсионного анализа……………………………………….…20
4.2. Однофакторный дисперсионный анализ…………………………………..20
Список литературы……………………………………………………………....21
Приложения……………………………………………………………………...22
Введение
Расчетно-графическая работа (РГР) предполагает применение основных приемов статистики для обработки массовой социально – экономической информации.
Программное обеспечение современных персональных компьютеров позволяет автоматизировать процесс расчетов. Наиболее эффективно использовать для этой цели табличный процессор Excel.
Excel предлагает широкий диапазон средств для анализа статистических данных. Такие встроенные функции, как СРЗНАЧ, МЕДИАНА, МОДА, могут быть полезны для проведения несложного анализа. Если встроенных статистических функций недостаточно, то можно обратиться к Пакету анализа.
Пакет анализа, являющийся надстройкой, содержит коллекцию функций и инструментов, расширяющих встроенные аналитические возможности Excel. В частности, пакет анализа можно использовать для создания гистограмм, ранжирования данных, извлечения случайных или периодических выборок из выбора данных, проведения регрессионного анализа, получения основных статистических характеристик выборки, генерации случайных чисел с различным распределением и для многих других расчетов.
Дата: 2019-12-22, просмотров: 298.