Условное высказывание – сложное высказывание, формулируемое обычно с помощью связки «если ..., то ...» и устанавливающее, что одно событие, состояние и т.п. является в том или ином смысле основанием или условием для другого.

Например: «Если есть огонь, то есть дым», «Если число делится на 9, оно делится на 3» и т.п.

Условное высказывание слагается из двух более простых высказываний. То из них, которому предпослано слово «если», называется основанием, или антецедентом (предыдущим); высказывание, идущее после слова «то», называется следствием, или консеквентом (последующим).

Утверждая условное высказывание, мы прежде всего имеем в виду, что не может быть так, чтобы то, о чем говорится в его основании, имело место, а то, о чем говорится в следствии, отсутствовало. Иными словами, не может случиться, чтобы антецедент был истинным, а консеквент – ложным.

В терминах условного высказывания обычно определяются понятия достаточного и необходимого условия: антецедент (основание) есть достаточное условие для консеквента (следствия), а консеквент – необходимое условие для антецедента.

Например, истинность условного высказывания «Если выбор рационален, то выбирается лучшая из имеющихся альтернатив» означает, что рациональность – достаточное основание для избрания лучшей из имеющихся возможностей и что выбор такой возможности есть необходимое условие его рациональности.

Типичной функцией условного высказывания является обоснование одного высказывания ссылкой на другое высказывание.

Например, то, что серебро электропроводно, можно обосновать ссылкой на то, что оно металл: «Если серебро – металл, оно электропроводно».

Выражаемую условным высказыванием связь обосновывающего и обосновываемого (основания и следствия) трудно охарактеризовать в общем виде, и только иногда природа ее относительно ясна. Эта связь может быть, во-первых, связью логического следования, имеющей место между посылками и заключением правильного умозаключения («Если все живые многоклеточные существа смертны, а медуза является таким существом, то она смертна»); во-вторых, законом природы («Если тело подвергнуть трению, оно начнет нагреваться»); в-третьих, причинной связью («Если Луна в новолуние находится в узле своей орбиты, наступает солнечное затмение»); в-четвертых, социальной закономерностью, правилом, традицией и т.п. («Если меняется общество, меняется также человек», «Если совет разумен, он должен быть выполнен»).

Со связью, выражаемой условным высказыванием, обычно соединяется убеждение, что консеквент с определенной необходимостью «вытекает» из антецедента и что имеется некоторый общий закон, сумев сформулировать который, мы могли бы логически вывести консеквент из антецедента.

Например, условное высказывание «Если висмут – металл, он пластичен» как бы предполагает общий закон «Все металлы пластичны», делающий консеквент данного высказывания логическим следствием его антецедента.

И в обычном языке, и в языке науки условное высказывание кроме функции обоснования может выполнять также ряд других задач: формулировать условие, не связанное с каким-либо подразумеваемым общим законом или правилом («Если захочу, разрежу свой плащ»); фиксировать какую-то последовательность («Если прошлое лето было сухим, то в этом году оно дождливое»); выражать в своеобразной форме неверие («Если вы решите эту задачу, я докажу великую теорему Ферма»), противопоставление («Если в огороде растет бузина, то в Киеве живет дядька») и т.п. Многочисленность и разнородность функций условного высказывания существенно затрудняет его анализ.

Употребление условного высказывания связано с определенными психологическими факторами. Так, обычно мы формулируем такое высказывание, только если не знаем с определенностью, истинны или нет его антецедент и консеквент. В противном случае его употребление кажется неестественным («Если вата – металл, она электропроводна»).

Условное высказывание находит очень широкое применение во всех сферах рассуждения. В логике оно представляется, как правило, посредством импликативного высказывания, или импликации. При этом логика проясняет, систематизирует и упрощает употребление «если ..., то ...», освобождает его от влияния психологических факторов.

Логика отвлекается, в частности, от того, что характерная для условного высказывания связь основания и следствия в зависимости от контекста может выражаться с помощью не только «если ..., то ...», но и других языковых средств.

Например: «Так как вода жидкость, она передает давление во все стороны равномерно», «Хотя пластилин и не металл, он пластичен», «Если бы дерево было металлом, оно было бы электропроводно» и т.п. Эти и подобные им высказывания представляются в языке логики посредством импликации, хотя употребление в них «если ..., то ...» было бы не совсем естественным.

Утверждая импликацию, мы утверждаем, что не может случиться, чтобы ее основание (антецедент) было истинным, а следствие (консеквент) – ложным.

Это определение предполагает, как и предыдущие определения связок, что всякое высказывание является либо истинным, либо ложным и что истинностное значение сложного высказывания зависит только от истинностных значений составляющих его высказываний и способа их связи.

Таким образом, для установления истинности импликации «если А, то В» достаточно выяснить истинностные значения высказываний А и В. Из четырех возможных случаев импликация истинна в следующих трех: 1) и ее основание, и ее следствие истинны; 2) основание ложно, а следствие истинно; 3) и основание, и следствие ложны.

Только в четвертом случае, когда основание истинно, а следствие ложно, импликация ложна.

Импликацией не предполагается, что высказывания А и В как-то связаны между собой по содержанию. В случае истинности В высказывание «если А, то В» истинно независимо от того, является А истинным или ложным и связано оно по смыслу с В или нет.

Например, истинным считаются высказывания: «Если на Солнце есть жизнь, то дважды два равно четыре», «Если Волга – озеро, то Токио – большой город» и т.п. Условное высказывание истинно также тогда, когда А ложно, и при этом опять-таки безразлично, истинно В или нет и связано оно по содержанию с А или нет. К истинным относятся высказывания: «Если Солнце – куб, то Земля – треугольник», «Если дважды два равно пять, то Токио – маленький город» и т.п.

В обычном рассуждении все эти высказывания вряд ли будут рассматриваться как имеющие смысл и еще в меньшей степени как истинные.

Хотя импликация полезна для многих целей, она не совсем согласуется с обычным пониманием условной связи. Импликация охватывает многие важные черты логического поведения условного высказывания, но она не является вместе с тем достаточно адекватным его описанием.

В последние полвека были предприняты энергичные попытки реформировать теорию импликации. При этом речь шла не об отказе от описанного понятия импликации, а о введении наряду с ним другого понятия, учитывающего не только истинностные значения высказываний, но и связь их по содержанию.

Эквивалентность

С импликацией тесно связана эквивалентность, называемая иногда «двойной импликацией».

Эквивалентность – сложное высказывание «А, если и только если В», образованное из высказываний А и В и разлагающееся на две импликации: «если А, то В» и «если В, то А». Например: «Треугольник является равносторонним, если и только если он является равноугольным». Термином «эквивалентность» обозначается и связка «..., если и только если ...», с помощью которой из двух высказываний образуется данное сложное высказывание. Вместо «..., если и только если ...» для этой цели могут использоваться «... в том и только в том случае, когда ...», «... тогда и только тогда, когда ...» и т.п.

Если логические связки определяются в терминах истины и лжи, эквивалентность истинна тогда и только тогда, когда оба составляющих ее высказывания имеют одно и то же истинностное значение, т.е. когда они оба истинны или оба ложны. Соответственно эквивалентность является ложной, когда одно из входящих в нее высказываний истинно, а другое ложно.

Категорические высказывания

При рассмотрении способов образования сложных высказываний из простых внутреннее строение простых высказываний во внимание не принималось. Они брались как неразложимые атомы, обладающие только одним свойством: быть истинными или ложными. Простые высказывания не случайно иногда именуются атомарными: из них, как из элементарных кирпичиков, с помощью логических связок «и», «или» и т.п. строятся разнообразные сложные («молекулярные») высказывания.

Теперь следует остановиться на вопросе о внутреннем строении, или внутренней структуре, самих простых высказываний: из каких конкретных частей они слагаются и как эти части связаны между собой.

Сразу же нужно подчеркнуть, что простые высказывания могут разлагаться на составные части по-разному. Результат разложения зависит от цели, ради которой оно осуществляется, т.е. от той теории логического вывода (логического следования), в рамках которой анализируются такие высказывания.

Далее будет рассматриваться лишь одна разновидность простых высказываний – категорические высказывания, по традиции называемые также категорическими суждениями.

Особый интерес к категорическим высказываниям объясняется прежде всего тем, что с исследования их логических связей началось развитие логики как науки. Кроме того, высказывания этого типа широко используются в наших рассуждениях.

Категорическое высказывание – это высказывание, в котором утверждается или отрицается наличие какого-то признака у всех или некоторых предметов рассматриваемого класса.

Например, в высказывании «Все динозавры вымерли» всем динозаврам (или, что то же самое, каждому из динозавров) приписывается признак «быть вымершими». В высказывании «Некоторые динозавры летали» способность летать приписывается некоторым динозаврам. В высказывании «Все кометы не астероиды» отрицается наличие признака «быть астероидом» у каждой из комет. В высказывании «Некоторые животные не являются травоядными» отрицается травоядность некоторых животных.

Если отвлечься от количественной характеристики, содержащейся в категорическом высказывании и выражающейся словами «все» и «некоторые», то получится два варианта таких высказываний: утвердительный и отрицательный. Их структура:

«S есть Р» и «S не есть Р»,

где буква S представляет имя того предмета, о котором идет речь в высказывании, а буква Р – имя признака, присущего или не присущего этому предмету.

Имя предмета, о котором говорится в категорическом высказывании, называется субъектом, а имя его признака – предикатом. Субъект и предикат именуются терминами категорического высказывания и соединяются между собой связками «есть» или «не есть» («является» или «не является» и т.п.).

Например, в высказывании «Солнце есть звезда» терминами являются имена «Солнце» и «звезда» (первый из них – субъект высказывания, второй – его предикат), а слово «есть» – связка.

Простые высказывания типа «S есть (не есть) Р» называются атрибутивными: в них осуществляется атрибуция (приписывание) какого-то свойства предмету.

Атрибутивным высказываниям противостоят высказывания об отношениях, в которых устанавливаются отношения между двумя или большим числом предметов: «Три меньше пяти», «Клев больше Одессы», «Весна лучше осени», «Париж находится между Москвой и Нью-Йорком» и т.п. Высказывания об отношениях играют существенную роль в науке, особенно в математике. Они не сводятся к категорическим высказываниям, поскольку отношения между несколькими предметами (такие, как «равно», «любит», «теплее», «находится между» и т.д.) не сводятся к свойствам отдельных предметов.

В категорическом высказывании не просто устанавливается связь предмета и признака, но и дается определенная количественная характеристика субъекта высказывания. В высказываниях типа «Все S есть (не есть) Р» слово «все» означает «каждый из предметов соответствующего класса». В высказываниях типа «Некоторые S есть (не есть) Р» слово «некоторые» употребляется в неисключающем смысле и означает «некоторые, а может быть, все». В исключающем смысле слово «некоторые» означает «только некоторые», или «некоторые, но не все». Различие между двумя смыслами этого слова можно продемонстрировать на примере высказывания «Некоторые звезды есть звезды». В неисключающем смысле оно означает «Некоторые, а возможно, и все звезды есть звезды» и является, очевидно, истинным. В исключающем же смысле данное высказывание означает «Лишь некоторые звезды являются звездами» и является явно ложным.

В категорических высказываниях утверждается или отрицается принадлежность каких-то признаков рассматриваемым предметам и указывается, идет ли речь обо всех этих предметах или же о некоторых из них. Возможны, таким образом, четыре вида категорических высказываний:

Все S есть Р – общеутвердительное высказывание,

Некоторые S есть Р – частноутвердительное высказывание,

Все S не есть Р – общеотрицательное высказывание,

Некоторые S не есть Р – частноотрицательное высказывание.

Категорические высказывания можно рассматривать как результаты подстановки каких-то имен в следующие выражения с «пробелами» (многоточиями): «Все... есть...», «Некоторые ... есть...», «Все ... не есть ...» и «Некоторые ... не есть ...». Каждое из этих выражений является логической постоянной (логической операцией), позволяющей из двух имен получить высказывание. Например, подставляя вместо многоточий имена «летающие» и «птицы», получаем, соответственно, следующие высказывания: «Все летающие есть птицы», «Некоторые летающие есть птицы», «Все летающие не есть птицы» и «Некоторые летающие не есть птицы». Первое и третье высказывания являются ложными, а второе и четвертое – истинными.

Аристотель истолковывал рассматриваемые четыре выражения именно как логические постоянные, не имеющие самостоятельного содержания и позволяющие из двух обладающих содержанием имен получать содержательные, являющиеся истинными или ложными высказывания.

В традиционной логике предполагалось также, что имена, подставляемые вместо многоточий (или переменных, если они используются вместо многоточий), не должны быть единичными или пустыми. Иначе говоря, высказывания типа «Платон – человек», «Все золотые горы – это горы» не относятся к категорическим в традиционном смысле, поскольку «Платон» – единичное имя, а «золотые горы» – пустое имя.

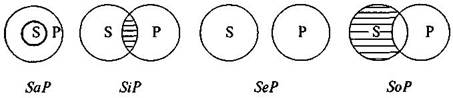
Обозначим оборот «Все ... есть ...» буквой а, оборот «Некоторые ... есть...» буквой i (первые гласные буквы латинского слова affirmo – утверждаю), оборот «Все ... не есть ...» буквой е и оборот «Некоторые ... не есть...» буквой о (гласные буквы латинского слова nego – отрицаю).

SaP – «Все S есть Р» – «Все жидкости упруги»,

SiP – «Некоторые S есть Р» – «Некоторые животные говорят»,

SeP – «Все S не есть Р» – «Все дельфины не есть рыбы»,

SoP – «Некоторые S не есть Р» – «Некоторые металлы не есть жидкости».

Отношения между терминами в четырех видах категорических высказываний представляются с помощью кругов Эйлера следующим образом:

Модальные высказывания

Модальные понятия – это понятия, позволяющие охарактеризовать высказывание или описываемую в нем ситуацию с той или иной точки зрения. К модальным относятся такие понятия, как «необходимо», «возможно», «доказуемо», «опровержимо», «хорошо», «плохо», «обязательно», «запрещено» и т.п.

Например, из немодального высказывания «Цирконий – металл» с помощью модальных понятий «необходимо», «доказуемо» и «хорошо» можно образовать модальные высказывания: «Необходимо, что цирконий – металл», «Доказуемо, что цирконий – металл» и «Хорошо, что цирконий – металл». В этих высказываниях связь предмета и признака оценивается с трех разных точек зрения.

В общем случае о предмете S можно просто сказать, что он имеет свойство Р. Но можно, сверх того, используя модальные понятия, уточнить, является ли эта связь S и Р необходимой или же она случайна, доказано ли, что S есть Р, или это только предполагается, хорошо ли, что S есть Р, или это плохо, и т.д. Результатами таких уточнений будут модальные высказывания разных типов. Общая их форма: М (S есть Р); вместо М в эту форму могут подставляться различные модальные понятия.

Модальную характеристику можно дать не только связям предметов и их признаков, но и связям других типов.

Например, из сложного высказывания «Если металлический стержень нагреть, он удлинится» можно получить модальные высказывания: «Необходимо, что, если металлический стержень нагреть, он удлинится», «Доказуемо, что, если металлический стержень нагреть, он удлинится» и т.п.

Модальное высказывание – это сложное высказывание, слагающееся из какого-то высказывания и его модальной характеристики. Модальное высказывание дает оценку входящего в него более простого высказывания или описываемой в последнем ситуации с той или иной точки зрения.

Например, модальное высказывание «Физически необходимо, что планеты Солнечной системы движутся по эллипсам» оценивает движение планет с точки зрения законов физики. Модальное высказывание «Доказано, что планеты Солнечной системы движутся по эллипсам» оценивает это движение с теоретико-познавательной точки зрения. Данное высказывание истинно с того времени, как Кеплер доказал, что траектории движения планет Солнечной системы имеют форму не круга, а эллипса.

Одно и то же высказывание может стать объектом нескольких последовательных модальных оценок с одной или разных точек зрения: «Хорошо, что доказано, что цирконий – металл» и т.п.

Всякое модальное высказывание содержит по меньшей мере одно модальное понятие. Никакого точного и полного перечня модальных понятий не существует. Их круг постоянно изменяется и не имеет четкой границы. В языке эти понятия могут выражаться в разных контекстах разными словами. Еще Аристотель отнес к модальным понятиям «необходимо», «возможно», «случайно» и «невозможно». Долгое время класс модальных высказываний исчерпывался высказываниями, включающими эти понятия. Уже в XX в. к модальным были причислены такие понятия, как «знает», «полагает», «доказуемо», «опровержимо», «обязательно», «разрешено», «хорошо», «плохо» и т.д.

Эти понятия очень различаются по своему конкретному содержанию. Общей для них является та роль, какую они играют в высказываниях: конкретизация фиксируемой в высказывании связи, уточнение ее характера, оценка ее с какой-то точки зрения.

Возьмем высказывание «Металлы проводят электрический ток». Оно допускает двойное уточнение: количественное и качественное. Можно воспользоваться какими-то из слов: «все», «некоторые», «большинство», «только один», «ни один» и т.п. и уточнить, о всех металлах идет речь или нет, всякого ли рода ток они проводят или же только одну его разновидность и т.д. Это будет количественная конкретизация высказывания.

Можно также попытаться конкретизировать качественный характер установленной в рассматриваемом высказывании связи. Для этого используются модальные понятия. Результатами их применения будут высказывания: «Необходимо, что металлы проводят ток», «Хорошо, что они проводят ток», «Опровергнуто, что это так» и т.п. Очевидно, что первое из этих модальных высказываний является истинным, а третье – ложным.

Виды модальных высказываний

Все модальные понятия распадаются на группы. Каждая из них дает характеристику с некоторой единой точки зрения. Так, для теоретико-познавательной конкретизации высказываний используются понятия «доказуемо», «опровержимо» и «неразрешимо», для нормативной – понятия «обязательно», «разрешено» и «запрещено», для оценочной – понятия «хорошо», «безразлично» и «плохо».

Точек зрения на тот или иной факт может быть сколько угодно. Число групп модальных понятий, выражающих эти точки зрения, также в принципе ничем не ограничено.

В логике рассматриваются только наиболее интересные и важные группы модальных понятий. К ним относятся, в частности, следующие группы модальных понятий: логические, физические, теоретико-познавательные, нормативные и оценочные модальные понятия.

В число логических модальных понятий входят: «логически необходимо», «логически возможно», «логически случайно», «логически невозможно» и др. Используя эти понятия, можно сформулировать такие, например, логические модальные высказывания: «Логически необходимо, что человек есть человек», «Логически возможно, что цирконий – металл», «Логически случайно, что Земля вращается», «Логически невозможно, что пять – простое число и пять одновременно не является простым числом». Во всех этих высказываниях связи, устанавливаемые в немодальных высказываниях, характеризуются с одной и той же – логической – точки зрения. В чем именно она состоит, выясняет раздел логики, занимающийся изучением логических модальных понятий. Сейчас, не входя в подробности, можно отметить, что все приведенные высказывания являются истинными.

К физическим модальным понятиям относятся: «физически необходимо», «физически возможно», «физически случайно», «физически невозможно» и др. Физические модальные понятия иногда именуются также казуальными или онтологическими (онтология – общая теория бытия). С помощью данных модальных понятий можно сформулировать такие, к примеру, физические модальные высказывания: «Физически необходимо, что металлы пластичны», «Физически возможно, что существуют еще не открытые химические элементы», «Физически случайно, будет ли через год в этот день солнечно» и «Физически невозможно, что вечный двигатель будет создан». Все эти высказывания характеризуют связи, устанавливаемые в соответствующих немодальных высказываниях с некоторой единой точки зрения – физической, или онтологической. Ее смысл уточняет раздел логики, занимающийся изучением физических модальных понятий.

Теоретико-познавательные модальные понятия называются также эпистемическими (от греч. episteme – знание). Группа этих понятий обширна и распадается на ряд подгрупп.

Можно выделить, в частности, эпистемические модальные понятия, относящиеся к доказуемости: «доказуемо», «опровержимо», «неразрешимо». С их помощью формулируются такие эпистемические модальные высказывания, как: «Доказуемо, что на Луне нет жизни», «Опровержимо, что сумма углов квадрата равна 180°», «Неразрешимо, каким будет автомобиль через сто лет». Еще одну подгруппу эпистемических модальных понятий составляют понятия, относящиеся к убеждению: «убежден», «сомневается», «отвергает». Доказуемость объективна и безлична, и если что-то считается доказуемым, то таковым оно является для каждого. Иначе обстоит дело с убеждениями. Они могут быть разными у разных людей; при разговоре о каких-то конкретных убеждениях надо указывать, кому именно они принадлежат. С помощью понятий «убежден», «сомневается» и «отвергает» можно сформулировать такие, к примеру, эпистемические модальные высказывания: «Аристотель был убежден, что у женщины меньше зубов, чем у мужчины», «Платон сомневался в жизнеспособности античной демократии» и «Сократ отвергал возможность уклонения от вынесенного ему смертного приговора».