В данной задаче рассматривается идеальный цикл двигателя внутреннего сгорания со смешанным подводом теплоты, впервые разработанный русским учёным Густавом Тринклером в 1902 году, в Московском высшем техническом училище. По этому циклу работают практически все современные двигатели с воспламенением от сжатия, которые в просторечии называются дизели (а совсем не по циклу Рудольфа Дизеля, как думают некоторые).
Основной задачей расчёта является определение параметров (р, v, T) в каждой из характерных точек диаграммы (1,2,3,4,5).
Для расчётов различных процессов используются формулы, представленные в таблице II.1. Полученные параметры заносятся в таблицу и затем используются для нанесения точек в масштабе на миллиметровой бумаге при построении p, v-диаграммы.
|
| 1 | 2 | 3 | 4 | 5 |
| v, м3/кг | |||||
| p, Мпа | |||||
| T, К |
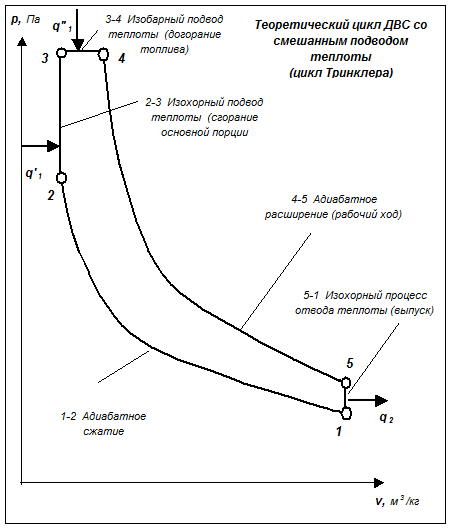
р, v – диаграмма цикла со смешанным подводом теплоты
Термический КПД цикла с подводом теплоты при постоянном объёме (цикл Отто), по которому работает подавляющее большинство бензиновых двигателей, определяется по формуле:
| h t = 1 - | 1 | ||
|
| e (k - 1) | ||
где h t – термический кпд цикла;
e – степень сжатия;
k – показатель адиабаты сжатия
Термический КПД цикла со смешанным подводом теплоты (цикл Тринклера), по которому работают практически все современные дизельные двигатели, определяется по формуле:
| h t = 1 - | 1 | * | l r k – 1 | |
|
| e (k - 1) | l - 1 + k l ( r - 1) | ||
где h t – термический кпд цикла;
e – степень сжатия;
k – показатель адиабаты сжатия
l - степень повышения давления в процессе подвода теплоты 2-3 (сгорания);
r – степень предварительного расширения в процессе подвода теплоты 3-4 (догорания).
З а д а ч а № 6.3
В данной задаче рассматривается идеальный цикл двигателя внутреннего сгорания с подводом теплоты при постоянном давлении, или цикл Отто. Определить максимальную температуру T3, в конце процесса сгорания, для бензинового двигателя, работающего по циклу с подводом теплоты при постоянном объёме, имеющего степень сжатия e, и степень повышения давления l. Если температура в начале процесса сжатия Т1 = 50оС, а давление р1 = 92 кПа, универсальная газовая постоянная R = 287 Дж/(кг*К), а коэффициент адиабаты k =1,4.
Данные для решения задачи взять из таблицы 6.1. Процесс сжатия представить в p, v-координатах на миллиметровой бумаге.
Таблица 6.1.
| Последняя цифра шифра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 | |
| e | 8,00 | 8,25 | 8,50 | 8,75 | 9,50 | 9,75 | 10,00 | 10,25 | 10,50 | 10,75 | |
| Предпоследняя цифра шифра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 | |
| l | 2,10 | 2,15 | 2,20 | 2,25 | 2,30 | 2,35 | 2,40 | 2,45 | 2,50 | 2,55 | |
З а д а ч а № 6.4
Определить параметры рабочего тела в характерных точках (1,2,3,4,5) идеального цикла поршневого двигателя внутреннего сгорания с изохорно-изобарным подводом теплоты (смешанный цикл), если известны давление p1 и температура t1 рабочего тела в начале сжатия. Степень сжатия e, степень повышения давления l и степень предварительного расширения r.
Определить термический КПД цикла. За рабочее тело принять воздух, считая теплоёмкость его в расчётном интервале температур постоянной. Универсальная газовая постоянная R = 287 Дж/(кг * К), коэффициент адиабаты k = 1,4.
Построить на миллиметровке в масштабе этот цикл в p,v-координатах. Дать пояснения к полученным графикам. Данные для решения взять из таблицы 6.2.
Таблица 6.2.
| Последняя цифра шифра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 | |
| p1, МПа | 0,090 | 0,092 | 0,094 | 0,096 | 0,098 | 0,100 | 0,102 | 0,104 | 0,106 | 0,108 | |
| t1, o C | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| e | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | |
| Предпоследняя цифра шифра | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 | |
L ,
1,50
1,55
1,60
1,65
1,70
1,75
1,80
1,85
1,90
1,95
r
1,50
1,45
1,40
1,35
1,30
1,25
1,20
1,15
1,10
1,05
З а д а ч а № 6.5 (продолжение задачи № 6.4)
При построении графика, по результатам расчёта задачи № 6.4 необходимо построить не менее 5-ти промежуточных точек для повышения точности построения графика. Затем провести через них линии графиков процессов 1-2 и 4-5. В этом случае используется основное уравнение адиабатного процесса
pvk = const
В любой точке процесса это равенство будет верным. Поэтому первоначально, в точке, где известны все параметры, вычисляется значение величины Const 1. Затем выбираются произвольные, удобные для построения, значения удельного объёма v1-2(1), v1-2(2), и т.д. по количеству выбранных точек. Зная v1-2(1), k и Const 1, вычисляется р1-2(1). Затем данные заносятся в таблицу, по ним строятся точки и проводится точная линия графика процесса адиабатного сжатия 1-2.
Точно такие же действия проводятся с процессом адиабатного расширения 4-5.
Раздел III . Теплопередача
Дата: 2019-12-22, просмотров: 399.