Цикл – это фрагмент программы, повторяемый многократно. В Паскале три оператора цикла – while, repeat и for. Все циклы имеют схожую структуру (Рис. 1)

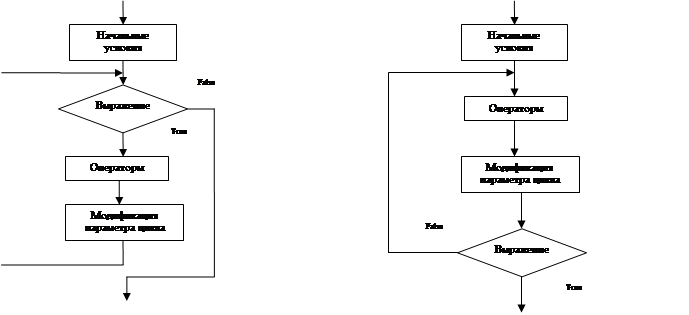
Рис. 1 Рис. 2
Операторы, ради многократного выполнения которых организуется цикл, называются телом цикла. Остальные операторы служат для управления процессом повторения вычислений: это начальные установки, проверка условия продолжения цикла и модификация параметра цикла. Один проход цикла называется итерацией. На этапе начальных установок (до входа в цикл) задаются значения переменных, которые в нем используются. Эти значения могут задаваться явно или неявно. Цикл завершается, если условие его продолжения не выполняется. Возможно принудительное завершение как текущей итерации (для этого применяется процедура continue ) , так и цикла в целом (процедура break и оператор goto). Передавать управление извне внутрь цикла не рекомендуется, потому что при этом не выполнятся начальные установки. Иными словами, выйти из цикла можно в любой момент, а войти – только в начало.
Цикл с предусловием while
В цикле с предусловием проверка условия продолжения цикла выполняется перед телом цикла
(Рис.2) Если при входе в цикл условие не выполняется, он не будет выполнен ни разу. Оператор цикла имеет вид
While выражение do оператор
Выражение должно быть логического типа. Если результат вычисления выражения равен true, выполняется расположенный после служебного слова do простой или составной оператор. Эти действия повторяются до того момента, пока результатом выражения не станет значение false. После окончания цикла управление передается следующему за ним оператору.
Задача 3.1. Печать таблицы значений функции
Написать программу печати таблицы значений функции sin для аргумента, изменяющегося в заданных пределах с заданным шагом.
Исходными данными являются начальное значение аргумента Х 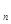 , конечное значение аргумента
, конечное значение аргумента 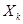 и шаг изменения аргумента dX. Все величины – вещественные и могут принимать любые значения на числовой оси. Результатом работы программы должна быть таблица, состоящая из двух столбцов – значений аргумента и соответствующих им значений функции.
и шаг изменения аргумента dX. Все величины – вещественные и могут принимать любые значения на числовой оси. Результатом работы программы должна быть таблица, состоящая из двух столбцов – значений аргумента и соответствующих им значений функции.
program tabl_fun;
var
Xn,Xk:real; {Начальное и конечное значения аргумента}
dx:real; {Шаг изменения аргумента}
x,y:real; {текущие значения аргумента и функции}
begin
writeln('Vvedite Xn,Xk,dX'); {Приглашение ко вводу данных}
readln(Xn,Xk,dX); {ввод исходных данных}
writeln('___________________________'); {заголовок таблицы}
writeln('______X_____|_______Y______');
writeln('___________________________');
x:=Xn; {первое значение аргумента =Хn}
while x<=Xk do begin {заголовок цикла}
y:=sin(x); {вычисление значения функции}
writeln('|',x:7:2,' |',y:7:2,' |'); {вывод строки табл.}
x:=x+dx; {переход к следующему значению аргумента} end;
writeln('___________________________') ;
readln; end.
Выполнить программу для Хn=-4, Xk=4, dx=1.
Индивидуальные задания
Задание 1
Вычислить и вывести на экран в виде таблицы значения функции, заданной графически (см. задание 1 лабораторной работы №2), на интервале от 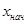 до
до 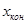 с шагом dx. Интервал и шаг задать таким образом, чтобы проверить все ветви программы. Таблицу снабдить заголовком и шапкой.
с шагом dx. Интервал и шаг задать таким образом, чтобы проверить все ветви программы. Таблицу снабдить заголовком и шапкой.
Задание 2
Для десяти выстрелов, координаты которых задаются с клавиатуры, вывести текстовые сообщения о попадании в мишень из задания 2 лабораторной работы «2.
Лабораторная работа №4. Организация циклов.(продолжение)
Задача 3.2. Вычисление суммы ряда
…………………………………………………………………………………………………………………
Написать программу вычисления значения функции sin с помощью степенного ряда с точностью 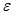 по формуле
по формуле
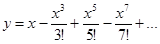
Этот ряд сходится на всей числовой оси. Для достижения заданной точности требуется суммировать члены ряда до тех пор, пока абсолютная величина очередного члена не станет меньше или равна 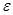 .
.
Запишем в общем виде формулу для вычисления n – го члена ряда:
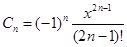
На первый взгляд может показаться, что придется организовать циклы для расчета факториала и степеней. При этом можно получить очень большие числа, при делении которых друг на друга произойдет потеря точности, поскольку количество значащих цифр, хранимых в ячейке памяти, ограничено. Кроме того, большие числа могут переполнить разрядную сетку.
Мы поступим по-другому. Легко заметить, что (n+1) – й член ряда вычисляется после n-го, поэтому программа получится более простой и эффективной, если находить член ряда не «с нуля», а умножением предыдущего члена на некоторую величину.
Найдем эту величину. Для этого сначала запишем формулу для (n+1)-го члена ряда, подставив в предыдущее выражение (n+1) вместо n:
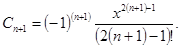
Теперь найдем выражение, на которое надо будет умножить C 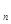 , чтобы получить С
, чтобы получить С 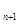 :
:
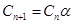
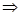
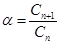 =
= 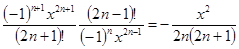
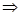
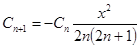
Запишем алгоритм вычисления суммы ряда в словесной форме:
1. Ввести исходные данные (аргумент и точность).
2. Задать начальные значения номеру члена ряда, первому члену ряда и сумме ряда.
3. Организовать цикл в котором:
1) Вычислить очередной член ряда;
2) Добавить его к сумме ряда;
3) Перейти к следующему члену ряда;
4) Проверить, достигнута ли точность вычислений.
4. Вывести значение функции.
Определить заранее, сколько членов ряда потребуется просуммировать для достижения точности, невозможно, поскольку при анализе условия выхода используется переменная, вычисляемая на каждой итерации цикла. Такие циклы потенциально опасны, поэтому для предотвращения зацикливания полезно предусмотреть аварийный выход из цикла по достижении некоторого максимально допустимого количества итераций с печатью предупреждающего сообщения.
Ниже приведен текст программы с комментариями. На каждой итерации требуется хранить значение одного члена ряда, поэтому все члены ряда формируются в одной и той же переменной с:
program sinus;
const MaxIter=500; {максимально допустимое количество итераций} 
var x,eps:double; {аргумент и точность}
c,y:double; {член ряда и его сумма}
n:integer; {номер члена ряда}
done:boolean; {признак достижения точности}
begin
writeln('Введите аргумент и точность:');
readln(x,eps);
done:=true;
c:=x; {первый член ряда}
y:=c; {начальное значение суммы}
n:=1;
while abs(c)>eps do begin
c:=-c*sqr(x)/2/n/(2*n+1); {очередной член ряда}
y:=y+c; {добавление члена ряда к сумме}
inc(n); {переход к следующему члену ряда}
if n<=MaxIter then continue;
writeln('ryd rasxoditsya');
done:=false;break {аварийный выход из цикла}
end;
if done then
writeln('Аргумент:',x:10:6,#13#10,
'Значение функции:',y:10:6,#13#10,
'Вычислено с точностью',eps:8:6,'за',n,'итераций');
readln;
end.
Первый член ряда равен х, поэтому, чтобы при первом проходе цикла значение второго члена вычислялось правильно, начальное значение n должно быть равно 1.Максимально допустимое количество итераций удобно задать с помощью именованной константы. Для аварийного выхода изх цикла применяется процедура break, которая обеспечивает переход к первому после цикла оператору. Символы #13#10 при выводе вызывают переход на следующую строку.
Контрольный пример для х=7.5 и eps=0,00001.
Индивидуальное задание
Вычислить и вывести на экран в виде таблицы значения функции, заданной с помощью ряда Тейлора, на интервале от 
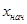 до
до 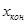 с шагом dx с точностью
с шагом dx с точностью 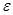 . Таблицу снабдить заголовком и шапкой. Каждая строка таблицы должна содержать значение аргумента, значение функции и количество просуммированных членов ряда.
. Таблицу снабдить заголовком и шапкой. Каждая строка таблицы должна содержать значение аргумента, значение функции и количество просуммированных членов ряда.
1. 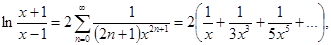
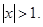
2. 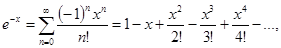
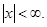
3. 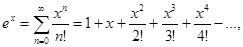
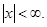
4. 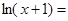
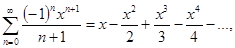
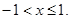
5. 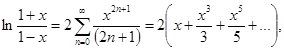
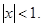
6. 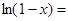
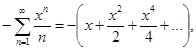
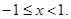
7. 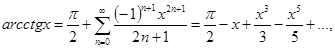
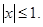
8. 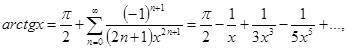 x>1.
x>1.
9. 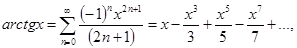
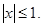
10. arthx= 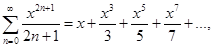
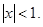
11. arthx= 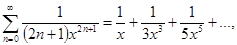
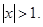
12. 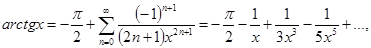
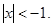
13. 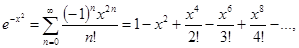
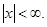
14. 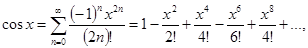
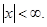
15. 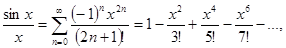
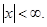
16. 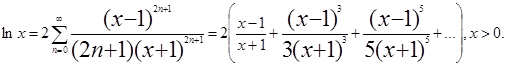
17. 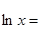

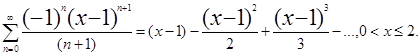
18. 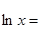
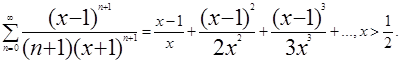

19. arcsinx = 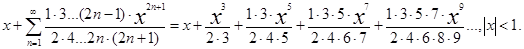
20. 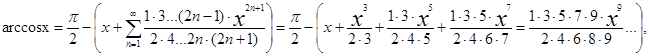
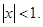
21. 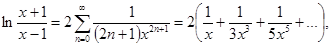
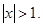
22. 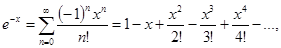
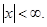
23. 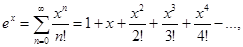
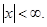
24. 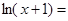
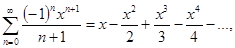
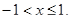
25. 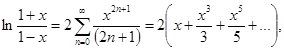
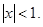
26. 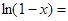
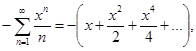
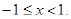
27. 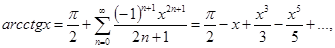
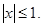
28. 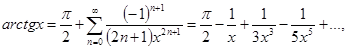 x>1.
x>1.
29. 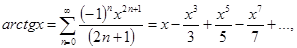
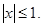
30. arthx= 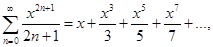
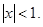
31. arthx= 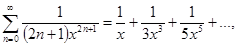
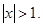
32. 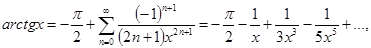
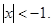
Дата: 2019-12-22, просмотров: 1217.