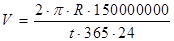МОУ «Лицей естественных наук города Кирова»
“Задачи по моделированию
средствами MS Excel”
г. Киров, 2009
Содержание
1. Введение ................................................................................................………………. 3
1.1 Психолого-педагогические особенности изучения темы
“Моделирования” в школьном курсе информатики
1.2 Обязательный минимум содержания образования по теме
“Моделирование и формализация”
1.3 Требования к уровню подготовки выпускников по теме
“Моделирование и формализация”
2. Основные понятия моделирования .......................................................……………. 7
3. Основные этапы моделирования ...........................................................……………. 10
4. Метод математических моделей ..........................................................…………….. 13
5. Задачи по моделированию из различных предметных областей ..........…………. 16
5.1 “Экономика” ……………………………………………………………………... 16
5.2 “Астрономия” ……………………………………………………………………. 24
5.3. “Физика” ………………………………………………………………………… 27
5.4 “Экология” ……………………………………………………………………….. 31
5.5 “Биология” ……………………………………………………………………….. 38
5.6 “География” ……………………………………………………………………… 44
6. Заключение …………………………………………………………………………... 45
7. Список литературы ………………………………………………………………….. 46
8. Приложение ………………………………………………………………………….. 47
Введение
Понятие модели
Модель — это некоторое упрощенное подобие реального объекта, явления или процесса.
Модель — это такой материальный или мысленно представляемый объект, который замещает объект-оригинал с целью его исследования, сохраняя некоторые важные для данного исследования типичные черты и свойства оригинала.
Хорошо построенная модель, как правило, доступнее для исследования, чем реальный объект (например, такой, как экономика страны, Солнечная система и т.п.). Другое, не менее важное назначение модели состоит в том, что с ее помощью выявляются наиболее существенные факторы, формирующие те или иные свойства объекта. Модель также позволяет учиться управлять объектом, что важно в тех случаях, когда экспериментировать с объектом бывает неудобно, трудно или невозможно (например, когда эксперимент имеет большую продолжительность или когда существует риск привести объект в нежелательное или необратимое состояние).
Таким образом, можно сделать вывод, что модель необходима для того, чтобы:
· понять, как устроен конкретный объект — каковы его структура, основные свойства, законы развития и взаимодействия с окружающим миром;
· научиться управлять объектом или процессом и определить наилучшие способы управления при заданных целях и критериях (оптимизация);
· прогнозировать прямые и косвенные последствия реализации заданных способов и форм воздействия на объект, процесс.
Структура — это определенный способ объединения элементов, составляющих единый сложный объект.
Система — это сложный объект, представляющий собой совокупность взаимосвязанных элементов, объединенных в некоторую структуру.
В учебнике “Информатика 9 класс” Н.В.Макаровой предложена следующая классификация моделей.
Классификация по области использования
|
|
| Модели |
|
| |||||||||
|
|
|
|
| ||||||||||
| Учебные | Опытные | Научно-технические | Игровые | Имитационные | |||||||||
Учебные: наглядные пособия, различные тренажеры, обучающие программы.
Опытные: уменьшенные или увеличенные копии исследуемого объекта для дальнейшего его изучения (модели корабля, автомобиля, самолета, гидростанции).
Научно-технические модели создают для исследования процессов и явлений (стенд для проверки телевизоров; синхротрон — ускоритель электронов и др.).
Игровые: военные, экономические, спортивные, деловые игры.
Имитационные: отражают реальность с той или иной степенью точности (испытание нового лекарственного средства в ряде опытах на мышах; эксперименты по внедрению в производство новой технологии).
Классификация с учетом фактора времени
|
| Модели |
| |||||
|
|
| ||||||
|
| |||||||
| Статические |
| Динамические | |||||
Статическая модель — модель объекта в данный момент времени.
Динамическая модель позволяет увидеть изменения объекта во времени.
Основные этапы моделирования
Моделирование — творческий процесс. Заключить его в формальные рамки очень трудно. В наиболее общем виде его можно представить поэтапно в следующем виде.
I этап. Постановка задачи
Описание задачи
Цель моделирования
Анализ объекта

 II этап. Разработка модели
II этап. Разработка модели
Информационная модель
Знаковая модель
Компьютерная модель
 III этап. Компьютерный
III этап. Компьютерный
Эксперимент
Экономика
Задача 1
Машиностроительный завод, реализуя продукцию по договорным ценам, получил определенную выручку, затратив на производство некоторую сумму денег. Определить отношение чистой прибыли к вложенным средствам.
Постановка задачи
Цель моделирования — исследовать процесс производства и реализации продукции с целью получения наибольшей чистой прибыли. Пользуясь экономическими формулами найти отношение чистой прибыли к вложенным средствам.
Чистая прибыль — это прибыль после уплаты налога. При расчете налога на прибыль необходимо учитывать его зависимость от уровня рентабельности. Примем, если уровень рентабельности не превышает 50%, то с прибыли предприятия взимается налог в 32%. Если же уровень рентабельности превышает 50%, то с соответствующей суммы прибыли налог взимается в размере 75%.
Объектом моделирования является процесс производства и реализации некоторой продукции.
Разработка модели
Основными параметрами объекта моделирования являются: выручка, себестоимость, прибыль, рентабельность, налог с прибыли.
Исходные данные:
выручка B;
затраты (себестоимость) S.
Другие параметры найдем, используя основные экономические зависимости. Значение прибыли определяется как разность между выручкой и себестоимостью P=B-S.
Рентабельность r вычисляется по формуле: 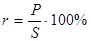 .
.
Прибыль, соответствующая предельному уровню рентабельности 50%, составляет 50% от себестоимости продукции S, т.е. S*50/100=S/2, поэтому налог с прибыли N определяется следующим образом:
если r<=50, то N=P*32/100 р., иначе N=S/2*32/100+(P-S/2)*75/100.
Чистая прибыль Рч=Р-N.
И, наконец, результат решения этой задачи — отношение чистой прибыли к вложенным средствам q= Рч/S.
Так выглядит электронная таблица в формате отображения формул:
| A. | B. | |
| 1. | ||
Рентабельность производства
Компьютерный эксперимент
1. Ввести в компьютерную модель исходные данные.
Например: B=3000; S=2000.
2. Исследовать, как изменяется отношение чистой прибыли к вложенным средствам, если менять только выручку, оставляя постоянной себестоимость.
3. Исследовать, как изменяется отношение чистой прибыли к вложенным средствам, если менять только себестоимость, оставляя постоянной выручку.
4. Как измениться модель, если налог вычисляется следующим образом:
| рентабельность | <=30% | от 30 до 70% | >70% |
| налог | 20% | 40% | 60% |
Изменится только формула в ячейке B8.
| 8. | Налог (р.) | =ЕСЛИ(B7<=30; B6*0,2;ЕСЛИ(B7<=70; B6*0,4; B6*0,6)) |
Анализ результатов
Полученная модель позволяет в зависимости от рентабельности определять налог с прибыли, автоматически пересчитывать размер чистой прибыли, находить отношение чистой прибыли к вложенным средствам.
Проведенный компьютерный эксперимент показывает, что отношение чистой прибыли к вложенным средствам увеличивается при увеличении выручки и уменьшается при увеличении себестоимости продукции.
Задача 2
Леспромхоз ведет заготовку деловой древесины. Известен ее первоначальный объем, ежегодный естественный прирост, а также годовой план заготовки. Какой объем деловой древесины на данной территории будет через год, через 2 года и т.д. — до тех пор, пока этот объем не станет меньше минимально допустимого значения.
Постановка задачи
Цель моделирования — показать динамику изменения объема деловой древесины, определить время до которого эти изменения будут происходить.
Объектом моделирования является процесс ежегодного изменения количества деловой древесины.
Количество деловой древесины в каждый следующий год вычисляется по количеству древесины предыдущего года до тех пор пока этот объем не станет меньше минимально допустимого значения (23000 м3).
Разработка модели
Допустим, исходные данные принимают следующие значения:
первоначальный объем V (м3) - 120000;
ежегодный прирост p (%) - 5,5;
годовой план заготовки R (м3) - 9500;
миним. допустимое значение (м3) - 23000.
Результатом является объем древесины через 1, 2, 3, ... года.
Объем древесины в каждом следующем году вычисляется по формуле:
Vi+1 = Vi + Vi*p/100-R
Так выглядит электронная таблица в режиме отображения формул:
| A. | B. | |
| 1. | ||
Задача 3
Фирма выпускает прогулочные и спортивные велосипеды. Ежемесячно сборочный цех способен собрать не более 600 прогулочных и не более 300 спортивных велосипедов. Качество каждого велосипеда проверяется на двух стендах А и В. Каждый прогулочный велосипед проверяется 0,3 ч на стенде А и 0,1 ч — на стенде В, а каждый спортивный велосипед проверяется 0,4 ч на стенде А и 0,3 ч — на стенде В. По технологическим причинам стенд А не может работать более 240 ч в месяц, а стенд В — более 120 ч в месяц. Реализация каждого прогулочного велосипеда приносит фирме доход в 50 руб., а каждого спортивного — 90 руб. Сколько прогулочных и сколько спортивных велосипедов должна ежемесячно выпускать фирма, чтобы ее прибыль была наибольшей? [3]
Постановка задачи
Цель моделирования — составить такой производственный план, который обеспечит максимальную прибыль.
Объект моделирования — процесс производства и реализации велосипедов
Разработка модели
Исходные данные:
x - количество прогулочных велосипедов, выпускаемых ежемесячно фирмой;
y - количество спортивных велосипедов.
Занятость стенда А составляет 0,3х+0,4y, что не должно превышать 240 ч.
Занятость стенда В составляет 0,1х+0,3y, что не должно превышать 120 ч.
Прибыль фирмы составляет S=50х+90у (руб.)
Итак, мы пришли к следующей модели: необходимо найти целые значения х и у, удовлетворяющие системе неравенств.
0,3х+0,4y £ 240 О1
0,1х+0,3y £ 120 О2
0 £ x £ 600 О3
0 £ y £ 300 О4
и такие, чтобы прибыль S=50х+90у была наибольшей.
Таким образом, задача нахождения наилучшего производственного плана свелась к задаче определения максимального значения функции S(x,y) при заданных ограничениях. (Такие задачи называются задачами условной оптимизации)
Электронная таблица в режиме отображения формул выглядит следующим образом:
| A. | B. | |
| 1. | Задача планирования | |
| 2. | Исходные данные | |
| 3. | х | |
| 4. | у | |
| 5. | Ограничения | |
| 6. | =0,3*B3+0,4*B4 | |
| 7. | =0,1*B3+0,3*B4 | |
| 8. | Результат | Прибыль |
| 9. | =50*B3+90*B4 | |
Компьютерный эксперимент
В среде электронных таблиц существует возможность автоматического поиска максимального (минимального) значения функции. Для этого:
1. введите значения исходных данных в ячейки В3 и В4 — любые целые числа, учитывая ограничения О3 и О4;
2. выберите команду [Сервис-Поиск решения...];
3. в появившемся диалоговом окне введите адрес ячейки, где содержится формула (функция для оптимизации);
4. укажите цель оптимизации (максимальное значение);
5. введите диапазон ячеек, посредством изменения значений которых будет достигнуто оптимальное значение целевой функции;
6. введите все ограничения.
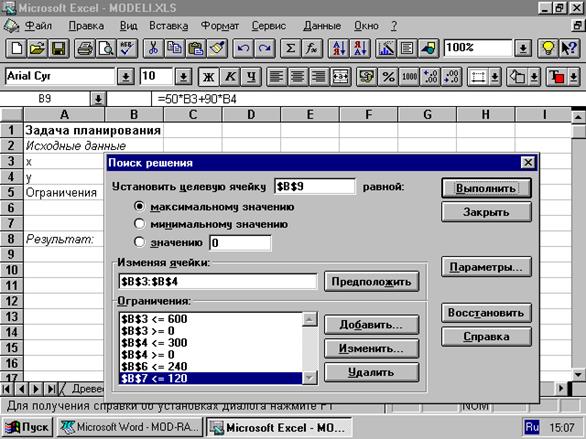
Результат выполнения выглядит так:
| A. | B. | |
| 1. | Задача планирования | |
| 2. | Исходные данные | |
| 3. | х | 480 |
| 4. | у | 240 |
| 5. | Ограничения | |
| 6. | 240 | |
| 7. | 120 | |
| 8. | Результат | Прибыль |
| 9. | 45600 | |
Анализ результатов
Значения, находящиеся в ячейках В3, В4 являются оптимальными для получения максимальной прибыли.
Продолжите компьютерный эксперимент
1. Что будет, если по технологическим причинам возможность работы стенда В уменьшится до 100 ч. в месяц.
2. Что будет, если доход от реализации каждого прогулочного велосипеда увеличится до 60 руб.
3. Что будет, если проверку спортивного велосипеда на стенде А ограничить до 0,3ч
Задача 4
В городе имеются два склада муки и два хлебозавода. Ежедневно с первого склада вывозится 50 т муки, со второго — 70 т. Эта мука доставляется на хлебозаводы, причем первый получает 40 т, второй — 80 т. Допустим, что перевозка одной тонны муки с первого склада на первый завод составляет 120 руб., с первого склада на второй завод — 160 руб., со второго склада на первый завод — 80 руб. и со второго склада на второй завод — 100 руб. Как нужно спланировать перевозки, чтобы их общая стоимость за один день была минимальной? [13]
Задача 5
Для полива трех полей колхоз использует насосную станцию. На первое поле требуется подать не менее 200 кубометров воды в сутки, на второе — не менее 300, на третье — не менее 350. Колхоз имеет право расходовать не более 1200 кубометров воды в сутки. Стоимость подачи одного кубометра воды на первое поле — 1570 руб., на второе поле — 1720 руб., на третье — 1930 руб. Сколько кубометров воды надо подать на каждое поле, чтобы затраты были наименьшими? [13]
Астрономия
Задача 1
Определите скорость движения планет по орбите. Для этого составьте компьютерную модель Солнечной системы.
Постановка задачи
Цель моделирования — определить скорость движения планет по орбите.
Объект моделирования — Солнечная система, элементами которой являются планеты. Внутреннее строение планет в расчет не принимается. Будем рассматривать планеты как элементы, обладающие следующими характеристиками:
название;
R - удаленность от Солнца (в астрономических единицах;
астроном. ед. — среднее расстояние от Земли до Солнца);
t - период обращения вокруг Солнца (в годах);
V - скорость движения по орбите (астр.ед./год), предполагая, что планеты
движутся вокруг Солнца по окружностям с постоянной скоростью.
Разработка модели
Исходные данные:
R - расстояние от планеты до Солнца,
t - период обращения планеты вокруг Солнца.
Т.к. планеты движутся вокруг Солнца по окружностям с постоянной скоростью, значение скорости найдем по формуле:

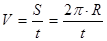 , (1)
, (1)
Данную модель реализуем в среде электронных таблиц. Диапазон ячеек D3:D11 содержат формулы. Так выглядит таблица в формате отображения формул:
| A. | B. | C. | D. | |
| 1. | ||||
Модель Солнечной системы
Компьютерный эксперимент
1. Выполните расчеты по формулам.
| A. | B. | C. | D. | |
| 1. |
Модель Солнечной системы | |||
| 2. | Планета | Расстояние от Солнца (астр.ед.) | Период обращения вокруг Солнца (год) | Скорость движения по орбите (астр.ед./год) |
| 3. | Меркурий | 0,387 | 0,24 | 10,132 |
| 4. | Венера | 0,723 | 0,62 | 7,327 |
| 5. | Земля | 1,000 | 1,00 | 6,283 |
| 6. | Марс | 1,524 | 1,88 | 5,093 |
| 7. | Юпитер | 5,203 | 11,86 | 2,756 |
| 8. | Сатурн | 9,539 | 29,46 | 2,034 |
| 9. | Уран | 19,18 | 84,02 | 1,434 |
| 10. | Нептун | 30,07 | 164,79 | 1,147 |
| 11. | Плутон | 39,44 | 247,7 | 1,000 |
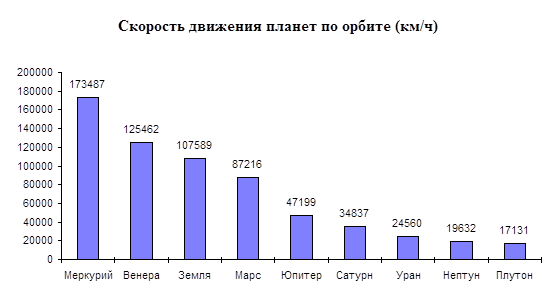
2. Вычислите скорость движения планет по орбите в км/ч и постройте график в виде столбчатой диаграммы для скоростей.
|
|
В данной модели формула (1) будет иметь вид:
(1 астрономическая единица = 150 млн. км.)
Анализ результатов
1. Проанализируйте результаты расчетов. Можно ли утверждать, что планеты, находящиеся ближе к Солнцу имеют большую скорость движения по орбите?
2. Представленная модель Солнечной системы является статической. При построении этой модели мы пренебрегали изменениями расстояния от планет до Солнца во время их движения по орбите. Чтобы знать, какая планета дальше и каковы примерные соотношения между расстояниями, этой информации вполне достаточно. Если же мы хотим определить расстояние между Землей и Марсом, то пренебрегать временными изменениями нельзя, и здесь придется использовать уже динамическую модель. Объясните, как вы понимаете термин динамическая модель?
Физика
Задача 1
При подъеме в гору “заглох” мотор у машины. Остановится ли машина на горе или же она будет скатываться вниз.
Постановка задачи
Цель моделирования — пользуясь знакомыми физическими законами движения тела под действием нескольких сил, исследовать данную ситуацию при различных значениях исходных данных.
Объектом моделирования является система, состоящая из двух компонентов: машина и дорога.
Разработка модели
Необходимо рассмотреть силы, действующие на машину в данной системе.
 y
y
 N
N



 Fтр
Fтр
 |


a

 a
a
x
 Fт a
Fт a

_ _
На машину действуют три силы: сила тяжести Fт=mg, сила трения Fтр и сила реакции опоры N.
По I закону Ньютона тело находится в состоянии покоя или движется прямолинейно и равномерно, если равнодействующая всех приложенных к телу сил равна нулю, т.е. F=0. _ _ _
II закон Ньютона в векторной форме записывается так: Fт+N+Fтр=0.
Запишем его в скалярной форме, для этого рассмотрим проекции сил
| на ось x: | на ось y: |
| (Fт)х=m*g*sina; Nx=0; (Fтр)х=-Fтр Уравнение: m*g*sina-Fтр=0 | (Fт)y=-m*g*cosa; Ny=N; (Fтр)y=0 Уравнение: -m*g*cosa+N=0 |
Fтр= m*g*sina
N= m*g*cosa
Так как Fтр=m*N, то m*g*sina=m* m*g*cosa
sina=m* cosa
tga=m
Итак, если tga>m, то машина стоит на месте, в противном случае она будет скатываться вниз.
Исходными данными являются:
m - коэффициент трения, 0<m<1;
a - угол наклона, 0<a<90. Так как в электронной таблице Excel функция tg находит значение tg от угла, выраженного в радианах, то при записи формулы предусмотрим перевод градусной меры угла в радианную.
Так выглядит таблица в формате отображения формул:
| A. | B. | |
| 1. | ||
Задача 2
На заданном расстоянии от пушки находится стена. Известны угол наклона пушки и начальная скорость снаряда. Попадет ли снаряд в стену?[5]
Постановка задачи
Цель моделирования — пользуясь знакомыми физическими законами движения тела, брошенного под углом к горизонту, исследовать данную ситуацию при различных значениях исходных данных.
Объектом моделирования является система, состоящая из двух компонентов: снаряд, брошенный под углом к горизонту, и стена. Подобрать начальную скорость и угол бросания так, чтобы брошенное тело (снаряд) достигло цели.
Разработка модели
Снаряд считаем материальной точкой.
Сопротивлением воздуха и размерами пушки пренебрегаем.
Исходные данные:
a - угол наклона пушки, 0<a<90 градусов;
V - начальная скорость снаряда (м/с), 0<V<1000;
S - расстояние от пушки до стены (м), S>0;
h - высота стены (м), h>0.
Результатом является одно из сообщений: “Снаряд попал в стену”, “Снаряд не попал в стену”.
Для определения попадания снаряда в стену надо найти высоту L снаряда на расстоянии S от пушки: ведь попадание снаряда в стену означает, что 0<L<h. Перемещение снаряда по горизонтали и вертикали:
x=V*t*cosa
y=V*t*sina-g*t2/2, где g-ускорение свободного падения (9,8 м/с2).
Определим, сколько времени понадобится снаряду, чтобы преодолеть расстояние S:
t=S/( V*cosa).
Подставив это значение t в выражение для y, получим значение:
L=S*tga-g*S2/(2*V2*cos2a).
Если L<0, то снаряд до стены не долетит. Если L>h, то снаряд перелетит через стену.
Так выглядит электронная таблица в формате отображения формул:
| A. | B. | |
| 1. | ||
Полет снаряда
Компьютерный эксперимент
1. Введите значения исходных данных:
Например: a=35; V=180; S=3000; h=6; g=9.8 и проанализируйте результат.
(Результат “Не попал”)
2. Найти такой угол наклона пушки, не изменяя другие параметры системы, при котором снаряд попадет в цель. (Результат a=32.6; a=32.7)
3. Найти такую скорость снаряда, не изменяя другие параметры системы, при котором снаряд попадет в цель. (Результат V=177)
4. Усовершенствуйте модель таким образом, чтобы результатом являлось одно из сообщений: “Снаряд попал в стену”, “Недолет”, “Перелет”.
Анализ результатов
Данная компьютерная модель позволяет проводить вычислительный эксперимент, взамен физическому. Меняя значения исходных данных, можно видеть все изменения происходящие в системе, производить расчет на поражение цели в зависимости от угла наклона пушки и скорости снаряда.
Задача 3
Две моторные лодки равномерно двигались по реке в направлении к озеру, в которое река впадает. Поравнявшись, они начали двигаться равноускоренно. Какая из лодок раньше дойдет до озера? [11]
Экология
Задача 1
Представьте себе, что на Земле останется только один источник пресной воды — озеро Байкал. На сколько лет Байкал обеспечит население всего мира водой?
Постановка задачи
Цель моделирования — определить количество лет, в течение которых Байкал обеспечит население всего мира водой, исследовать построенную модель.
Объектом моделирования является система, состоящая из двух компонентов: озеро Байкал и население Земли.
Зная количество воды в Байкале, численность населения Земли и потребляемость воды на 1 человека, можно найти на сколько лет ее хватит. При составлении этой модели мы не учитываем возможные изменения климатических условий. Мы также считаем постоянными численность населения Земли и потребляемость воды на 1 чел. в день. (Человечество потребляет на свои нужды огромное количество пресной воды. Основными ее потребителями являются промышленность, сельское и коммунально-бытовое хозяйство. Объем потребляемой воды зависит от уровня жизни, составляя от 3 до 700 л на одного человека.)
Разработка модели
Для построения математической модели определим исходные данные. Обозначим:
V - объем озера Байкал 23000 км3;
N - население Земли 6 млрд. чел.;
p - потребление воды в день на 1 человека (в среднем) 300 л.
Так как 1л. = 1 дм3 воды, необходимо выполнить перевод V воды озера из км3 в дм3. V (км3) = V * 109 (м3) = V * 1012 (дм3)
Результат — количество лет, за которое население Земли использует воды Байкала, обозначим g. Итак, g=(V*1000000000000)/(N*p*365)
Так выглядит электронная таблица в режиме отображения формул:
| A. | B. | |
| 1. | ||
Задача 2
Известны ежегодные показатели рождаемости и смертности некоторой популяции. Рассчитайте, до какого возраста могут дожить особи одного поколения.
Постановка задачи
Цель моделирования — исследовать изменение численности поколения популяции в зависимости от времени, определить возраст до которого могут дожить особи одного поколения популяции.
Объектом моделирования является процесс ежегодного изменения количества одного поколения популяции, который зависит от рождаемости популяции и ее смертности.
Разработка модели
Так как ежегодная рождаемость популяции соответствует количеству особей одного поколения в популяции, то исходными данными являются:
x - количество особей в 1 год;
p - ежегодная смертность (%).
Численность популяции в каждом следующем году рассчитывается по формуле: xi+1=xi - xi*p/100. Расчет производим до тех пор, пока значение xi не станет <1.
Так выглядит электронная таблица в режиме отображения формул:
| A. | B. | |
| 1. | ||
Задача 3
Определите, как будет меняться плотность популяции голубя в течение 5 ближайших лет, если предварительные наблюдения позволили установить, что ее плотность составляет 130 особей/га. За период размножения (у голубя раз в году) из одной кладки яиц в среднем выживает 1,3 детенышей. Смертность голубя постоянна, в среднем за год погибает 27% особей. При увеличении плотности популяции до 300 особей/га и выше смертность составляет 50%.
Постановка задачи
Цель моделирования — исследовать процесс изменения плотности популяции с учетом ее рождаемости и смертности.
Объект моделирования — процесс изменения плотности популяции.
Плотность популяции — это число особей, приходящаяся на единицу площади или объема жизненного пространства. Измерением плотности пользуются в тех случаях, когда важнее знать не конкретную величину популяции в тот или иной момент времени, а ее динамику, то есть ход изменений численности во времени.
Рождаемость характеризует способность популяции к увеличению численности за счет размножения особей. Показатель рождаемости — это число новых особей (также яиц, семян), родившихся (вылупившихся, отложенных) в популяции за определенный промежуток времени.
Смертность — это показатель, противоположный рождаемости. Смертность, как и рождаемость, выражается числом особей, погибших за данный период времени, но чаще в виде относительной или удельной величины. Такой величиной может быть процент особей, погибших в единичный отрезок времени.
Разработка модели
Известно начальное значение плотности популяции.
Плотность популяции к началу следующего года есть ее плотность к началу данного года плюс рождаемость и минус смертность.
Рождаемость зависит от плотности самок и плодовитости. Предположим, что в популяции равное количество самок и самцов, то, зная плотность популяции, можно определить плотность самок (плотность самок=1/2 плотности популяции). Плодовитость известна по условию задачи. Число особей, погибших за год — это процент (смертности) от общей плотности популяции. Смертность популяции зависит так же и от величины плотности популяции.
Исходные данные:
плотность популяции (P) - 130 особей/га;
плодовитость - 1,3 детеныша в год.
Остальные показатели рассчитываются следующим образом:
плотность самок = P/2;
рождаемость (R) = плотность самок * плодовитость;
смертность (S) = P * удельная смертность;
где удельная смертность голубя = 27% в год, если P<300,
в противном случае она равна 50%;
Плотность популяции в каждом следующем году рассчитывается по формуле:
Pi+1 = Pi + Ri - Si.
Так выглядит электронная таблица в режиме отображения формул:
| A. | B. | C. | D. | E. | F. | |
| 1. | ||||||
Задача 4
Как определить размер популяции рыбы в озере, используя метод мечения и повторного отлова.
Постановка задачи
Объект моделирования — популяция рыбы.
Для измерения обилия популяций испытано много различных методов. К наиболее распространенным относится метод мечения и повторного отлова (для подвижных животных). Этот метод — включает отлов животных, его мечение (без причинения вреда), пойманных животных подсчитывают и выпускают. Через некоторое время животных снова отлавливают и подсчитывают их общее число и отдельно число меченых. Численность популяции оценивают по формуле:
О = В1*В2/М,
где О - общая численность популяции,
В1 - число особей при 1 отлове,
В2 - число особей при 2 отлове,
М - число меченых животных пойманных при 2 отлове.
Используя данный метод, решите предложенную задачу при следующих значениях исходных данных: В1=625; В2=873; М=129.
Результат: 4230 особей.
Биология
Задача 1
Для производства вакцины на заводе планируется выращивать культуру бактерий. Известно, что если масса бактерий - x г., то через день она увеличится на (a-bx)x г., где коэффициенты a и b зависят от вида бактерий. Завод ежедневно будет забирать для нужд производства вакцины m г. бактерий. Для составления плана важно знать, как изменяется масса бактерий через 1, 2, 3, ..., 30 дней..[5]
Постановка задачи
Цель моделирования — исследовать изменения массы бактерий, в зависимости от ее начального значения.
Объектом моделирования является процесс ежедневного изменения количества вакцины с учетом выращивания и использования бактерий для производства вакцины.
Разработка модели
Исходные данные:
a и b - коэффициенты;
x0 - начальная масса бактерий;
m - масса бактерий, забираемых для нужд производства;
Количество бактерий каждого следующего дня зависит от количества бактерий предыдущего дня и вычисляется по формуле:
xi+1= xi+(a-b*xi)*xi-m - масса бактерий в следующий день.
Результатами являются значения массы бактерий через 1, 2, 3, 4 ... 30 дней.
Так выглядит электронная таблица в режиме отображения формул:
| A. | B. | |
| 1. | ||
Задача 2
Составить модель биоритмов для конкретного человека от указанной текущей даты (дня отсчета) на месяц вперед с целью дальнейшего анализа модели. На основе анализа индивидуальных биоритмов прогнозировать неблагоприятные дни, выбирать благоприятные дни для разного рода деятельности. [4]
Постановка задачи
Цель моделирования — составить модель биоритмов для конкретного человека от указанной текущей даты на месяц вперед с целью ее дальнейшего анализа.
Объектом моделирования является любой человек, для которого известна дата его рождения.
В жизни человека бывают творческие и бесплодные, счастливые и несчастливые дни, дни, когда он бывает в приподнятом или в подавленном настроении. Существует теория, что жизнь человека подчиняется циклическим процессам, называемым биоритмами. Эти циклы описывают три стороны самочувствия человека: физическую, эмоциональную и интеллектуальную. Биоритмы характеризуют подъемы и спады нашего состояния. Многие полагают, что “взлетам” графика, представляющего собой синусоидальную зависимость, соответствуют более благоприятные дни. Дни, в которые график переходит через ось абсцисс, являются критическими, т.е. неблагоприятными. Если у каких-либо двух (или у всех трех) биологических ритмов совпадают критические дни, то такой день называется дважды (трижды) критическим.
За точку отсчета трех биоритмов берется день рождения человека.
Физический биоритм характеризует жизненные силы человека, т.е. его физическое состояние. Периодичность ритма 23 дня.
Эмоциональный биоритм характеризует внутренний настрой человека, его возбудимость, способность эмоционального восприятия окружающего. Продолжительность периода эмоционального цикла равна 28 дням.
Третий биоритм характеризует мыслительные способности, интеллектуальное состояние человека. Цикличность его — 33 дня.
Разработка модели
Исходные данные:
дата рождения человека;
дата отсчета;
период физического цикла = 23 дня;
период эмоционального цикла =28 дней;
период интеллектуального цикла =33 дня.
Указанные циклы описываются следующими формулами:
физический цикл Rф(x)= 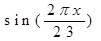
эмоциональный цикл Rэ(x)= 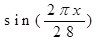
интеллектуальный цикл Rи(x)= 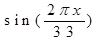 ,
,
где переменная x соответствует возрасту человека в днях.
Для нахождения x необходимо из текущей даты вычесть дату рождения человека.
Результатом является диаграммы биоритмов человека: физического, эмоционального и интеллектуального, построенные в одной системе координат.
Компьютерный эксперимент
1. Введите значения исходных данных в таблицу в ячейки C3:C7.
| A. | B. | C. | D. | E. | |
| 1. | |||||
География
Задача 1
Какова будет численность населения России в 2010 году? [16]
Постановка задачи
Объектом моделирования является процесс изменения численности населения в зависимости от времени. На этот процесс влияют многие факторы: экология, состояние медицинского обслуживания, экономическая ситуация в стране, международная обстановка и многое другое. Обобщив демографические данные, ученые вывели функцию, выражающую зависимость численности населения от времени:
f(t)= 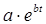
где коэффициента a и b для каждого государства свои,
e основание натурального логарифма.
Эта формула лишь приближенно отражает реальность. Для нахождения значений коэффициентов a и b можно воспользоваться статистическим справочником. Взяв из справочника значения f(t) (численность населения в момент времени t), можно приближенно подобрать a и b так, чтобы теоретические значения f(t), вычисляемые по формуле, не сильно отличались от фактических данных в справочнике.
6. Заключение
Тема “Моделирование” является очень важной в курсе информатики, так как дает учащимся возможность провести исследовательскую работу, выполнить анализ полученных результатов, обратить внимание на конечность алгоритма, оценить точность модели, столкнуться с погрешностью приближенных вычислений, увидеть взаимосвязь различных наук и дисциплин, получить удовлетворение от выполненной работы.
Использование компьютера как инструмента учебной деятельности дает возможность переосмыслить традиционные подходы к изучению многих вопросов естественнонаучных дисциплин, усилить экспериментальную деятельность учащихся, приблизить процесс обучения к реальному процессу познания, основанному на технологии моделирования.
Решение задач из различных областей деятельности человека на компьютере базируются не только на знаниях учащимися технологии моделирования, но, естественно, и на знаниях данной предметной области. В связи с этим, предложенные уроки по моделированию целесообразнее проводить после изучения учащимися материала на общеобразовательном предмете, учителю информатики необходимо сотрудничать с учителями разных образовательных областей. Известен опыт проведения бинарных уроков, т.е. уроков, проводимых учителем информатики совместно с учителем-предметником.
Предложенные задачи можно использовать при изучении курса информатики в 9-11 классах.
Список литературы
1. Извозчиков В.А., Бережной Л.Н., Слуцкий А.М. Межпредметные связи и информатика (методические рекомендации) — Санкт-Петербург, 1992.
2. Машбиц Е.И. Психолого-педагогические проблемы компьютеризации обучения — М., Педагогика, 1988.
3. Симонов А.С. Экономика на уроках математики. — М., Школа-Пресс, 1999.
4. Учебник “Информатика. 9 класс.” под ред. Макаровой Н.В. — Санкт-Петербург, ПИТЕР КОМ, 1999.
5. Гейн А.Г., Житомирский В.Г. и др. “Основы информатики и вычислительной техники” пробный учебник для 10-11 классов средней школы — М., Просвещение, 1992.
6. Семакин И., Залогова Л., Русаков С., Шестакова Л. "Информатика” учебник по базовому курсу — М., ООО Лаборатория Базовых Знаний, 1998.
7. Гисин В.Б., Коновалов В.П., “Программно-методический комплекс № 4 по курсу информатики. Элементы компьютерного моделирования” — М., АО КУДИЦ, 1994.
8. Дагене В.А., Григас Г.К., Аугутис К.Ф. “100 задач по программированию”, книга для учащихся, пер. с лит. — М., Просвещение, 1993.
9. Криксунов Е.А., Пасечник В.В., Сидорин А.П. “Экология 9 класс”, учебник для общеобразовательных учебных заведений — М., Дрофа, 1995.
10.Криксунов Е.А., Королев Ю.Б., Пасечник В.В., “Экология 9 класс”, рабочая тетрадь — М., Дрофа, 1996.
11. Кикоин И.К., Кикоин А.К. “Физика. 9 класс”, учебник — М., Просвещение,1990.
12.Петросян В.Г., Газарян Р.М. Межпредметные связи и решение задач//
Информатика и образование. 1998 №8.
13.Островская Е.М. Моделирование на компьютере// Информатика и образование. 1998 №7, 8; 1999 №1.
14.Пономарева Е.А. Основные закономерности развития мышления// Информатика и образование. 1999 №8.
15.Бешенков С.А., Лыскова В.Ю., Матвеева Н.В., Ракитина Е.А. Формализация и моделирование// Информатика и образование. 1999 №6.
16.Гусева О.Л., Миронова Н.Н. Excel для Windows. Практические работы// Информатика и образование. 1996 №5.
Приложение
МОУ «Лицей естественных наук города Кирова»
“Задачи по моделированию
средствами MS Excel”
г. Киров, 2009
Содержание
1. Введение ................................................................................................………………. 3
1.1 Психолого-педагогические особенности изучения темы
“Моделирования” в школьном курсе информатики
1.2 Обязательный минимум содержания образования по теме
“Моделирование и формализация”
1.3 Требования к уровню подготовки выпускников по теме
“Моделирование и формализация”
2. Основные понятия моделирования .......................................................……………. 7
3. Основные этапы моделирования ...........................................................……………. 10
4. Метод математических моделей ..........................................................…………….. 13
5. Задачи по моделированию из различных предметных областей ..........…………. 16
5.1 “Экономика” ……………………………………………………………………... 16
5.2 “Астрономия” ……………………………………………………………………. 24
5.3. “Физика” ………………………………………………………………………… 27
5.4 “Экология” ……………………………………………………………………….. 31
5.5 “Биология” ……………………………………………………………………….. 38
5.6 “География” ……………………………………………………………………… 44
6. Заключение …………………………………………………………………………... 45
7. Список литературы ………………………………………………………………….. 46
8. Приложение ………………………………………………………………………….. 47
Введение
Дата: 2019-12-22, просмотров: 448.