Второстепенная балка рассчитывается как многопролетная неразрезная балка таврового сечения. Конструктивная и расчетная схема второстепенно балки показана на рис.
Расчетные пролеты:
— крайние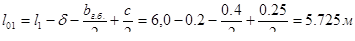 
;
— средние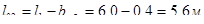 
;
Расчетные нагрузки на 1м определим с помощью таблицы 7, путем умножения их значений на шаг второстепенных балок, т.е.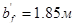 
. Тогда постоянная нагрузка (от собственной массы перекрытия и второстепенной балки) с учетом коэффициента надежности по назначению здания, 
:
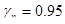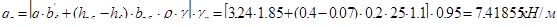
Временная нагрузка с учетом :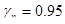
.
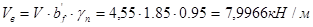Полная нагрузка:
.
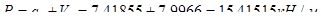Статический расчет балки. Расчетные усилия в сечениях балки определяются с учетом их перераспределения за счет появления пластических деформаций. Изгибающие моменты:
- в первом пролете
;
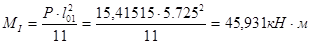- на первой промежуточной опоре
;
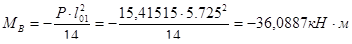- в средних пролетах и на средних опорах
;
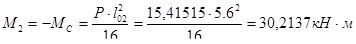Для средних пролетов балки определяют минимальные изгибающие моменты от невыгодного расположения временной нагрузки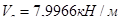 
на смежных пролетах при отношении
.
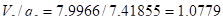Тогда в сечении 6 на расстоянии от опоры 
:
,
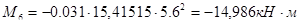в сечении 7 на расстоянии от опоры 
:
.
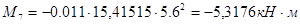Поперечные силы:
- на опоре А:
;
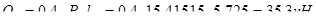- на опоре В слева:
;
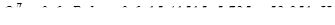- на опоре В справа и на остальных опорах:
.
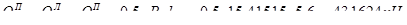Определение высоты сечения второстепенной балки. Высота сечения балки определяется по опорному моменту при значении коэффициента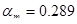 
и 
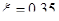(для элементов, рассчитываемых с учетом перераспределения внутренних усилий):
,
.
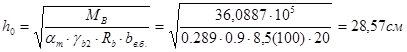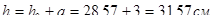Принимаем ранее принятую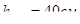 
, тогда 
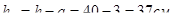. Проверяем достаточность высоты сечения второстепенной балки для обеспечения прочности бетона при действии главных сжимающих усилий:
.
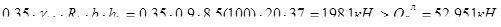Условие удовлетворяется, следовательно, высота сечения второстепенной балки достаточна.
Расчет по прочности сечений, нормальных к продольной оси балки. Отношение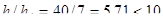 
, значит в расчет может быть введена ширина полки таврового сечения в пролете балки. 
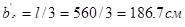,что больше, чем 
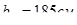. Изгибающий момент, воспринимаемый сжатой полкой сечения и растянутой арматурой:
.
Т.к.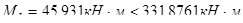 
, то нейтральная ось пересекает полку и пролетное сечение балки рассчитывается как прямоугольное. Определение площади сечения нижней рабочей продольной арматуры в крайнем пролете балки:
,
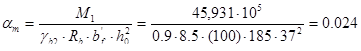по приложению Ⅹ [2] определяем табличные коэффициенты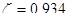 
, 
.
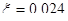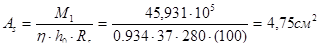
Принимаем 2ф18 класса А-II c As= 5,09 см2. Коэффициент армирования:
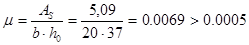
Определение площади сечения арматуры в среднем пролете балки:
,
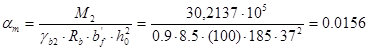табличные коэффициенты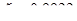 
, 
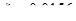, тогда
.
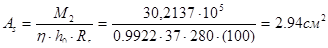Принимаем 2ф14 класса А-II c As= 3.08 см2. Растянутую рабочую арматуру в опорных сечениях второстепенных балок монолитных перекрытий конструируют в виде рулонных сеток с поперечной рабочей арматурой, раскатываемых вдоль главных балок. Размеры расчетного сечения: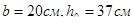 
. Определение рабочей арматуры в сечении над второй от края опорой:
,
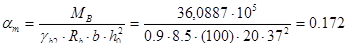по приложению Ⅹ [2] определяем табличные коэффициенты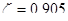 
, 
.
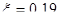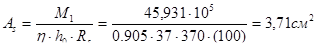
Принимаем 20ф5Вр-1 c As= 3,92 см2.
Коэффициент армирования:
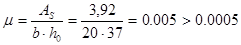
В сечении сеток, располагаемых в два слоя на ширине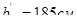 
, требуемый шаг стержней 
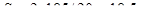. Ставим две рулонные сетки:
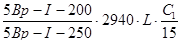
Обрывы надопорных сеток назначаем на следующих расстояниях: для одного конца сетки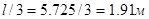 
; для другого 
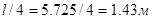. Определение рабочей арматуры в сечении над остальными опорами:
,
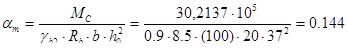по приложению Ⅹ [2] определяем табличные коэффициенты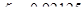 
, 
.
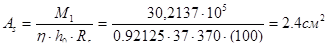
Принимаем 14ф5 Вр-1 c As= 2.75 см2.
Требуемый шаг стержней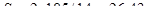 
.
Принимаем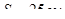 
.
Рулонные сетки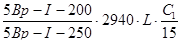 
с обрывами на 1.8 и 1.45 м от оси опор. За пределами длины надопорных сеток, т.е. на расстоянии 
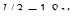от опор, минимальный отрицательный момент должен быть воспринят верхними стержнями арматурного каркаса балки и бетоном. Отрицательный изгибающий момент в сечении на расстоянии 
от опоры находим по интерполяции между величинам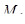и 
и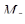 
:
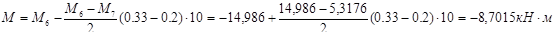
При прямоугольном сечении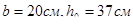 
:
,
, 
.
.
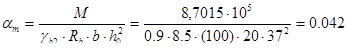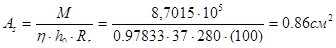Принимаем 2ф10 класса А-II c As= 1.57 см2.
Расчет по прочности сечений, наклонных к продольной оси балки.
Расчет ведется на действие поперечной силы. Прочность элемента по наклонному сечению на действие поперечной силы считается обеспеченной при отсутствии наклонных стержней, если соблюдается условие: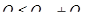 
,
где: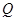 
- поперечная сила в элементе; 
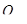- сумма осевых усилий в поперечных арматурных стержнях, пересекаемых сечением; 
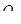- проекция на нормаль к продольному направлению элемента равнодействующей усилий в сжатой зоне бетона; Наибольшее значение поперечной силы на первой промежуточной опоре слева 
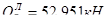. Вычисляем проекцию расчетного наклонного сечения (С) на продольную ось.
Влияние свесов сжатой полки:
,
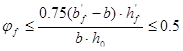где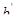 
принимается не более 
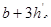, тогда
.
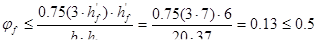Вычисляем:
,
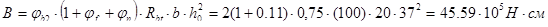где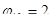 
- для тяжелого бетона; 
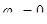- коэффициент, учитывающий влияние продольных сил.
В расчетном наклонном сечении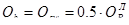 
, тогда
.
Принимаем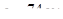 
, тогда 
;
,
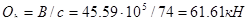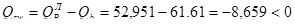т.е. поперечные стержни по расчету не требуются. Диаметр поперечных стержней устанавливаем из условия сварки в продольными стержнями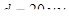 
и принимаем 
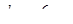класса А-I c 
.
Число каркасов два,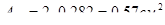 
.
Шаг поперечных стержней по конструктивным условиям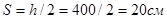 
, но не более 15 см. Для всех приопорных участков промежуточных и крайней опор балки принимаем 
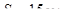. В средней части пролета (на расстоянии 
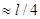) шаг 
.
Производим проверку по сжатой полосе между наклонными трещинами:
; 
;
;
.
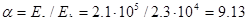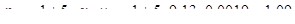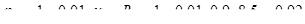Условие:
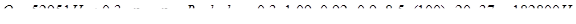
— удовлетворяется.
Расчет по прочности сечений, наклонных к продольной оси балки, на действие изгибающего момента.
Прочность наклонного сечения на действие изгибающего момента обеспечивается надлежащим заанкерованием рабочей продольной арматуры на опорах балки и в местах обрыва продольных стержней. Продольные стержни растянутой и сжатой арматуры должны быть заведены за нормальное к продольной оси элемента сечение, в котором они учитываются с полным расчетным сопротивлением, на длину не менее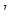 
, равную:
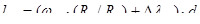, но не менее 
.
На свободной опоре балки напряжение продольной арматуры теоретически равно нулю, и длина заделки стержней периодического профиля ф18 А-II за грань должна быть не менее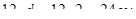 
. Конструктивно глубина заделки балки в стену 25см. В среднем пролете балки до опоры доводятся два нижних продольных стержня
Ф14 А-II. Расчет по раскрытию трещин и по деформациям для конструкций монолитного ребристого перекрытия допускается не производить, т.к. на основании практики из применения установлено, что величина раскрытия трещин в них не превышает предельно допустимых величин и жесткость конструкций в стадии эксплуатации достаточна.
Исходные данные
Сетка колонн 7,4×6,0м, число этажей-3, высота этажа 3.0м, размер оконного проема принимаем 1.5×1.4м, толщина наружной стены 510 мм.
Материалы: кирпич (обожженная глина пластического прессования) по [3]; раствор марки М50. Кладка сплошная, плотность кладки 18.000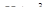 
, ширина оконного проема 
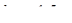, высота 
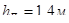. Ширина рассчитываемого простенка 
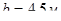. Грузовая площадь
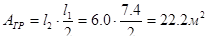(см. рис. 19),
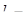шаг колонн в поперечном направлении,
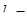шаг колонн в продольном направлении.
Нагрузка от верхних этажей, перераспределившись, прикладывается в центр тяжести сечения простенка. Нагрузка от перекрытия рассматриваемого этажа приложена с
фактическим эксцентриситетом. Расстояние от точки приложения опорной реакции балки до внутренней поверхности стены
.
Принимаем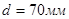 
.
9.2 Сбор нагрузок на простенок для сборного варианта перекрытия
1. Нагрузка от покрытия и перекрытия в уровне верха плиты перекрытия 1-го этажа:
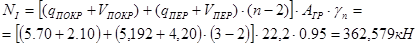
здесь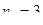 
- количество этажей;
2. Расчетная нагрузка от веса кирпичной кладки в уровне верха плиты перекрытия 1-го этажа:
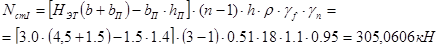
3. Нагрузка от кладки над оконным проемом 1-го этажа:
4. Нагрузка от перекрытия 1-го этажа:
.
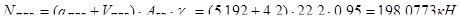5. Полная расчетная нагрузка в сечении II-II:
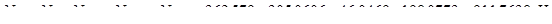
Определим расчетные моменты:
- момент в сечении I-I:
;
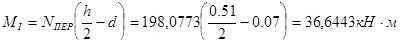- момент в сечении II-II:
,
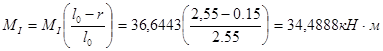где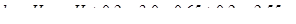 
.
Расчетные характеристики
Площадь сечения простенка:
.
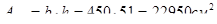Коэффициент условия работы кладки 
. Расчетное сопротивление кладки на растворе М50 с 
. Упругая характеристика кладки 
. Расчетная линия простенка
.
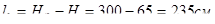Гибкость простенка
.
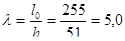По таблице 18 [3] определяем коэффициент продольного изгиба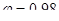 
(по интерполяции). Найденное значение 
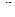принимается для средней трети высоты простенка. Расчетное сечение I-I (см. рис), поэтому значение для сечений I-I принимаем откорректированным 
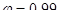. Расчетный эксцентриситет продольной силы:
.
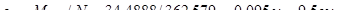Проверку несущей способности простенка в сечении I-I производим из расчета его на внецентренное сжатие по формуле: 
,
Здесь: 
- площадь сжатой части сечения. Для прямоугольного сечения:
;
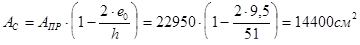- коэффициент продольного изгиба для внецентренно сжатых элементов: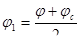 
;
где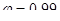 
; 
- коэффициент продольного изгиба для сжатой части сечения, определяемый по таблице 18[3] в зависимости от:
,
где
; 
;
;
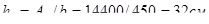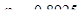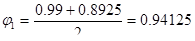При
( 
) 
; 
,
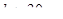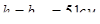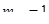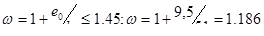тогда несущая способность простенка в сечении I-I:
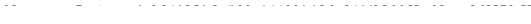
Прочность простенка обеспечена.
Список литературы
1. СНиП 2.03.01-84*. Бетонные и железобетонные конструкции. Госстрой СССР, 1989г.
2. СНиП 2.01.07-85. Нагрузки и воздействия. Госстрой СССР, 1986г.
3. СНиП II-22-81. Каменные и армокаменные конструкции. Госстрой СССР, 1983г.
4. Байков В.Н., Сигалов Э.Е. Железобетонные конструкции: общий курс: Учебник для вузов М.: Стройиздат, 1991г.
5. Бондаренко В.М., Суворкин Д.Г. Железобетонные и каменные конструкции: Учебник для студентов ВУЗов по спец. ПГС. М.: Высшая школа, 1987г.
6. Бондаренко В.М., Судницин А.И. Расчёт строительных конструкций. Железобетонные и каменные конструкции. М.: Высшая школа, 1988г.
7. Манриков А.П. Примеры расчёта железобетонных конструкций: Учебное пособие для техникумов. М.: Стройиздат, 1989г.
8. Пособие по проектированию каменных и армокаменных конструкций (к СНиП II-22-81) Госстрой СССР, 1989г.
9. Пособие по проектированию бетонных и железобетонных конструкций из тяжёлых и лёгких бетонов без преднапряжения арматуры (к СНиП 2.03.01-84). Госстрой СССР, 1986г.
10. Пособие по проектированию предварительно напряжённых железобетонных конструкций из тяжёлых и лёгких бетонов (к СНиП 2.03.01-84). Часть 1. Госстрой СССР, 1988г.
11. Пособие по проектированию предварительно напряжённых железобетонных конструкций из тяжёлых и лёгких бетонов (к СНиП 2.03.01-84). Часть 2. Госстрой СССР, 1988г.
Дата: 2019-12-22, просмотров: 263.
