Существует 2 способа описания термодинамических свойств растворов – с помощью активностей компонентов и с помощью избыточных термодинамических функций. Эти способы тесно связаны между собой.

Избыточная термодинамическая функция – это положительный или отрицательный избыток какого-либо термодинамического свойства реального раствора над тем же свойством гипотетического идеального раствора при одинаковых значениях параметров. Обозначают их верхними индексами Е.

Если в качестве стандартного состояния выбрать чистый компонент, и концентрации представлять в виде мольных долей, то для компонента s:

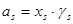 (1.2)

Коэффициент активности 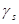 может быть выражен через соответствующий избыточный химический потенциал:

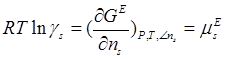 (1.3)

Прологарифмировав (1.2) с учётом (1.3) получим:

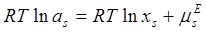 (1.4)

Таким образом, для определения активности необходимо знать избыточный химический потенциал (или избыточную энергию Гиббса), а для аналитического представления концентрационной и температурной зависимости термодинамических свойств растворов нужно знать соответствующую зависимость 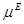 или .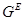

Обычно для описания реальных растворов применяют модель идеального раствора, при этом 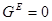. Однако, в реальном растворе законы Рауля и Генри, а также равенства типа 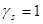(или 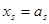) выполняются только в чрезвычайно узких диапазонах концентраций при 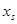→0, или 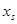→1 (то есть в бесконечно разбавленных растворах).

Существует теория, включающая в себя понятия «идеальный» и «предельно разбавленный» растворы, как частные случаи. Это обобщённая теория «регулярных» растворов (далее – ОТРР). С её позиций области, в которых реальный раствор является регулярным (так называемые области «граничной регулярности») располагаются также по краям диапазона концентраций, но они существенно шире.

Регулярным называется модельный раствор, при образовании которого может выделяться или поглощаться теплота, но не изменяется объём, а энтропия смешения компонентов которого равна энтропии смешения идеальных газов.

Для регулярного раствора, состоящего из m компонентов, в рамках ОТРР выполняется соотношение:

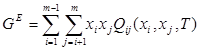 (1.5)

Здесь 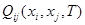- энергия смешения. Для идеального раствора 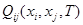=0, а в областях граничной регулярности энергия смешения не зависит от мольных долей компонентов.

Если в 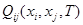отдельно выделить концентрационно зависимую составляющую и разложить её в ряд Тейлора, то получится уравнение:

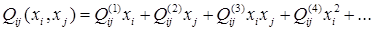 (1.6)

При этом каждое из слагаемых в правой части будет зависеть от температуры.

Как показывает математическая обработка экспериментальных данных, для бинарных растворов достаточно первых трёх параметров 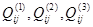, чтобы в большинстве случаев корректно аппроксимировать термодинамические функции смешения системы. При этом  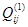имеет смысл энергии смешения компонентов i и j в растворе на основе компонента i,  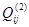– энергии смешения компонентов i и j в растворе на основе компонента j. Обе эти величины – это термодинамические характеристики областей граничной регулярности двойной системы. А  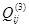– это параметр, учитывающий отклонение от регулярности вне этих областей.

Установлено, что для бинарных металлических систем достаточно двух параметров, поэтому принято принимать 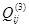=0. С учётом этого, выражение для химического потенциала компонента s в растворе, содержащем m компонентов, запишется так:

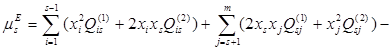
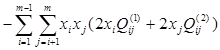 (1.7)

Формулы ОТРР позволяют успешно описывать термодинамические свойства металлических, неметаллических и смешанных систем [10].