Алгоритм расчета разработан с учетом [11, 12, 13, 14, 15].
Напряженность в точке М пространства 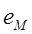 , кВ/м от заряда i - го проводника
, кВ/м от заряда i - го проводника 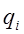 , Кл равна:
, Кл равна:
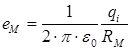
где 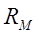 – расстояние, м от точки М в пространстве до i - ого заряда
– расстояние, м от точки М в пространстве до i - ого заряда 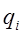 ;
;
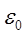 –диэлектрическая проницаемость вакуума,
–диэлектрическая проницаемость вакуума, 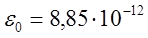 Ф/м.
Ф/м.
Чтобы получить формулы для расчета мгновенных, максимальных и действующих значений напряженности электрического поля в пространстве, окружающем линию электропередачи, сначала совмещаем комплексную плоскость с плоскостью поперечного сечения линии.
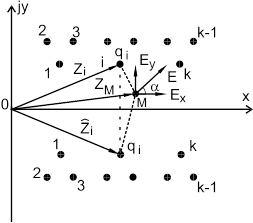
| Рисунок 2.1 - Расположение проводников линии электропередачи в комплексной плоскости |
Затем для данной точки М плоскости записываем уравнения для горизонтальной 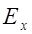 и вертикальной
и вертикальной 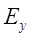 составляющих, создаваемых линейными зарядами ( k ) проводников линии
составляющих, создаваемых линейными зарядами ( k ) проводников линии
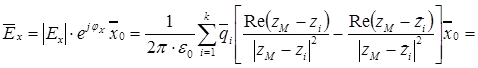
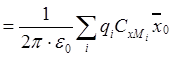 ; (2.1)
; (2.1)
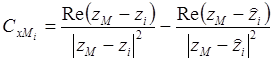
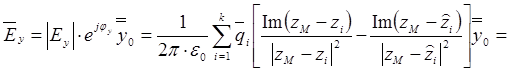
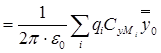 ,
,
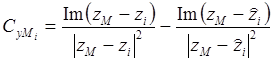
где 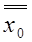 – единичный вектор в направлении оси х;
– единичный вектор в направлении оси х;
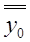 – единичный вектор в направлении оси y;
– единичный вектор в направлении оси y;
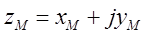 – координата точки М, в которой вычисляется напряженность;
– координата точки М, в которой вычисляется напряженность;
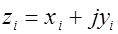 – координаты i - ого проводника линии электропередачи;
– координаты i - ого проводника линии электропередачи;
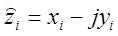 – координаты зеркально отраженного заряда i - ого проводника линии;
– координаты зеркально отраженного заряда i - ого проводника линии;
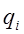 - комплексные заряды на i - ых проводниках ЛЭП, которые вычисляется по уравнениям Максвелла в матричной форме:
- комплексные заряды на i - ых проводниках ЛЭП, которые вычисляется по уравнениям Максвелла в матричной форме:
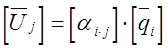 , откуда
, откуда 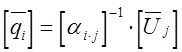
где 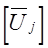 – столбцовая матрица комплексных напряжений, В;
– столбцовая матрица комплексных напряжений, В;
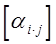 – столбцовая матрица потенциальных коэффициентов;
– столбцовая матрица потенциальных коэффициентов;
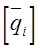 – столбцовая матрица комплексных зарядов, проводников, Кл.
– столбцовая матрица комплексных зарядов, проводников, Кл.
переходя к мгновенным значениям
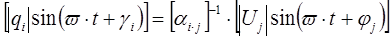 , (2.2)
, (2.2)
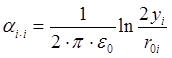 ;
;
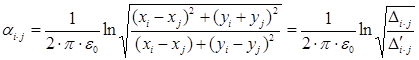
где 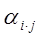 – потенциальные коэффициенты;
– потенциальные коэффициенты;
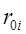 – радиус i - го проводника, м;
– радиус i - го проводника, м;
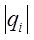 и
и 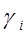 – соответственно амплитудное значение и фаза заряда на i - ом проводнике;
– соответственно амплитудное значение и фаза заряда на i - ом проводнике;
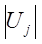 и
и 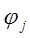 – соответственно амплитуда и фаза напряжения на i - ом проводнике.
– соответственно амплитуда и фаза напряжения на i - ом проводнике.
Амплитудное значение фазного напряжения на проводниках линии определяется через действующее значение номинального линейного напряжения как 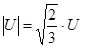
На основании (2.1) и (2.2) можно заключить, что мгновенные значения вертикальной и горизонтальной составляющих напряженности в данной точке пространства изменяются во времени по закону синуса:
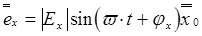 ; (2.3)
; (2.3)
 ;
;
Мгновенное значение результирующей напряженности согласно рисунку 2.1:
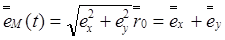 (2.4)
(2.4)
где 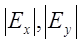 и
и 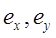 – соответственно амплитуды и мгновенные значения горизонтальной и вертикальной составляющих напряженности поля;
– соответственно амплитуды и мгновенные значения горизонтальной и вертикальной составляющих напряженности поля;
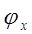 и
и 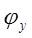 – фазы горизонтальной и вертикальной составляющих напряженности поля, которые, как следует из (2.1) равны;
– фазы горизонтальной и вертикальной составляющих напряженности поля, которые, как следует из (2.1) равны;
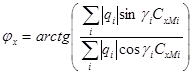
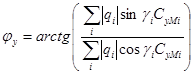 (2.5)
(2.5)
Записывая результирующую напряженность как вектор, изменяющийся во времени и на комплексной плоскости (пространстве), получим
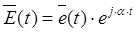 (2.6)
(2.6)
где с учетом (2.3)
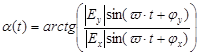 (2.7)
(2.7)
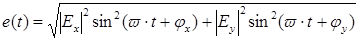 (2.8)
(2.8)
где 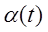 – направление результирующего вектора
– направление результирующего вектора 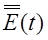 в данный момент времени;
в данный момент времени;
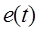 – мгновенное значение этого вектора.
– мгновенное значение этого вектора.
Анализ выражений (2.7) и (2.8) показывает, что в каждой точке пространства, окружающего проводники линии электропередачи, конец результирующего вектора напряженности электрического поля 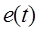 , описывает эллипс (рисок 2.2 б) за период времени, равный периоду изменения напряжения на фазах линии электропередачи.
, описывает эллипс (рисок 2.2 б) за период времени, равный периоду изменения напряжения на фазах линии электропередачи.

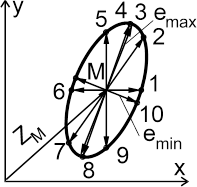
| а | б |
Рисунок 2.2 - Изменение электрического поля в точке М плоскости поперечного сечения линии: а - во времени горизонтальной Ex и вертикальной Ey составляющих; б - в пространстве направления a и во времени Т результирующей напряженности Е
| 1) a = 0°, T=0; 2) a = 54,7°, T = 45; 3) Emax, a = 68,34°, T=82,98; 4) a = 70,5°, T=90; 5) a = 90°, T=135; 6) a = 180°, T=180; 7) a = 234°, T=225; 8) a = 250,5°, T=270; 9) a = 270°, T=315; 10) Emin, a = - 21,66°, T= -7,02; |
Таким образом, в какие - то моменты времени величина результирующего вектора 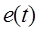 принимает максимальное и минимальное значения. Чтобы найти эти экстремальные значения, нужно взять производную по времени от выражения и приравнять ее к нулю:
принимает максимальное и минимальное значения. Чтобы найти эти экстремальные значения, нужно взять производную по времени от выражения и приравнять ее к нулю:
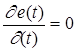 (2.9)
(2.9)
Решая уравнение (2.9), с учетом (2.8) получаем значения времени, при которых 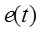 принимает экстремальные значения:
принимает экстремальные значения:
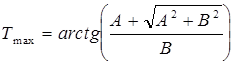
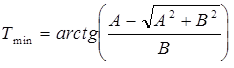 (2.10)
(2.10)
где
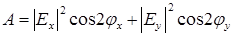 ;
;
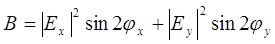
Подставляя (2.10) в (2.7) и (2.8), находим экстремальные значения результирующей напряженности поля:
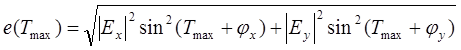 (2.11)
(2.11)
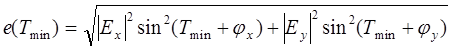
а так же их направления:
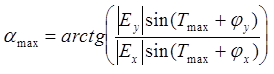 (2.12)
(2.12)
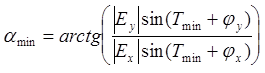
Действующее значение напряженности в точке М пространства найдем по формуле изменения периодической величины:
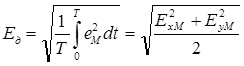 (2.13)
(2.13)
Таким образом, горизонтальная 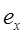 и вертикальная
и вертикальная 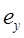 составляющие внешнего поля, создаваемого проводниками линии, синусоидальны, тогда как закон изменения во времени результирующего поля
составляющие внешнего поля, создаваемого проводниками линии, синусоидальны, тогда как закон изменения во времени результирующего поля 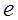 не синусоидален.
не синусоидален.
На рисунке 2.2 в качестве примера, представлены графики, показывающие изменение величин 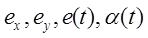 во времени и пространстве, для случая
во времени и пространстве, для случая 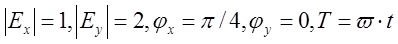
Дата: 2019-12-10, просмотров: 344.