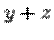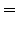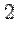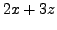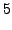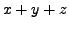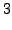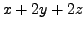Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Пример 1. Использовать метод Гаусса для решения линейной системы.

 

 

Решение: Расширенная матрица имеет вид 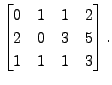Метод состоит из следующих шагов:

1. Поменяем местами первое и второе уравнение, чтобы коэффициент у х в первом уравнении не был равен нулю

1. Разделим первое уравнение на 2, чтобы коэффициент у х стал равен 1

1. Первое уравнение умножаем на -1 и складываем с третьим уравнением

1. Второе уравнение умножаем на -1 и складываем с третьим .

1. Умножим третье уравнение на -2/3

Последнее уравнение дает 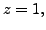второе уравнение дает теперь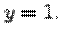

Наконец, первое уравнение дает

Следовательно, решение исходной системы х = 1, у = 1, z = 1.

AT-M Ad

Решение системы с бесконечным множеством решений

Пример 2 Решить систему линейных уравнений .

 

Решение: Расширенная матрица имеет вид 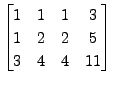и метод исключения неизвестных осуществляется следующим образом:

1. Первое уравнение умножим на -1 и сложим со вторым

2. Умножим первое уравнение на -3 и сложим с третьим

1. Умножим второе уравнение на -1 и сложим с третьим

Таким образом, y = 2 - z, x = 1, где z любое число. Т.е. система имеет бесконечное число решений.

Решение системы не имеющей решений

Пример 3

Решить линейную систему.

 

Решение: В этом случае, расширенная матрица имеет вид 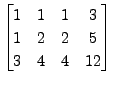и метод исключения неизвестных осуществляется следующим образом:

1. Умножим первое уравнение на -1 и сложим со вторым .

1. Умножим первое уравнение на -3 и сложим с третьим уравнением .

1. Второе уравнение умножим на -1 и сложим с третьим

Третьего уравнения системы имеет вид-

Это равенство не выполняется ни при каких значениях неизвестных 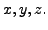Таким образом, система не имеет решений.

Примечание Обратите внимание, что для решения линейной системы уравнений методом Гаусса 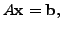нужно применять только элементарные преобразования расширенной матрицы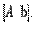

Метод Крамера

Система линейных уравнений имеет вид:

a₁₁ x₁ + a₁₂ x₂ +... + a_1n x_n = b₁,

a₂₁ x₁ + a₂₂ x₂ +... + a_2n x_n = b₂, (5.1)

... ... ... ...

a_m1 x₁ + a_m1 x₂ +... + a_mn x_n = b_m.

Здесь а_{i j} и b_i (i = ; j = 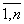) - заданные, а x_j - неизвестные действительные числа.

Метод Крамера состоит в том, что мы последовательно находим главный определитель системы (5.3), т.е. определитель матрицы А

D = det (a_{i j})

и n вспомогательных определителей D _i (i= 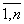), которые получаются из определителя D заменой i-го столбца столбцом свободных членов.

Формулы Крамера имеют вид:

D × x _i = D _i ( i = 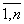). (5.4)

Из (5.4) следует правило Крамера, которое дает исчерпывающий ответ на вопрос о совместности системы (5.3): если главный определитель системы отличен от нуля, то система имеет единственное решение, определяемое по формулам:

x _i = D _i / D.

Если главный определитель системы D и все вспомогательные определители D _i = 0 (i= 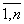), то система имеет бесчисленное множество решений. Если главный определитель системы D = 0, а хотя бы один вспомогательный определитель отличен от нуля, то система несовместна.

Пример 2.14. Решить методом Крамера систему уравнений:

x₁ + x₂ + x₃ + x₄ = 5,

x₁ + 2x₂ - x₃ + 4x₄ = -2,

2x₁ - 3x₂ - x₃ - 5x₄ = -2,

3x₁ + x₂ +2x₃ + 11 x₄ = 0.

Ссылка на вычисление определителей on-line.

Решение. Главный определитель этой системы

 

значит, система имеет единственное решение. Вычислим вспомогательные определители D _i ( i = 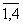), получающиеся из определителя D путем замены в нем столбца, состоящего из коэффициентов при x_i, столбцом из свободных членов:

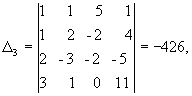
Отсюда x₁ = D ₁/D = 1, x₂ = D ₂/D = 2, x₃ = D ₃/D = 3, x₄ = D ₄/D = -1, решение системы - вектор С=(1, 2, 3, -1)^T.

Матричный метод

Если матрица А системы линейных уравнений невырожденная, т.е. det A ≠ 0, то матрица А имеет обратную, и решение системы совпадает с вектором C = A^-1B. Иначе говоря, данная система имеет единственное решение. Отыскание решения системы по формуле X=C, C=A^-1B называют матричным способом решения системы, или решением по методу обратной матрицы.

Пример 2.15. Решить матричным способом систему уравнений

x₁ - x₂ + x₃ = 6,

2x₁ + x₂ + x₃ = 3,

x₁ + x₂ +2x₃ = 5.

Решение. Обозначим

Тогда данная система уравнений запишется матричным уравнением AX=B. Поскольку , то матрица A невырождена и поэтому имеет обратную:

.

Для получения решения X мы должны умножить вектор-столбец B слева на матрицу A: X = A^-1B. В данном случае

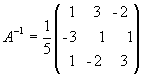
и, следовательно,

.

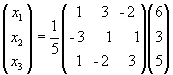Выполняя действия над матрицами, получим:

x₁ = 1/5(1×6+3×3-2×5) = 1/5 (6+9-10) = 1,

x₂ = 1/5 (-3×6 +1×3 - 1×5) = 1/5 (- 18 + 3 + 5) = -2,

x₃ = 1/5 (1×6 - 2×3 + 3×5) = 1/5 (6 -6 + 15) = 3.

Итак, X = (1, -2, 3)^T.