В настоящее время при расчете настроек регуляторов локальных систем широко используются простые динамические модели промышленных объектов управления. В частности, использование моделей инерционных звеньев первого или второго порядка с запаздыванием для расчета настроек регуляторов обеспечивает в большинстве случает качественную работу реальной системы управления.
В зависимости от вида переходной характеристики (кривой разгона) задаются чаще всего одним из двух видов передаточной функции объекта управления:
- в виде передаточной функции инерционного звена первого порядка
(1)
где –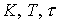 
коэффициент усиления, постоянная времени и запаздывание, которые должны быть определены в окрестности номинального режима работы объекта.
Для объекта управления без самовыравнивания передаточная функция имеет вид
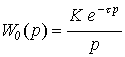(2)
По кривой разгона оценивается характер объекта управления (с самовыравниванием или без) и определяются параметры соответствующей передаточной функции. Передаточную функцию вида (1) рекомендуется применять для объектов управления с явно выраженной доминирующей постоянной времени (одноемкостный объект). Перед началом обработки кривую разгона рекомендуется пронормировать (диапазон изменения нормированной кривой 0 – 1) и выделить из ее начального участка величину чистого временного запаздывания.
Методы первого порядка
Передаточная функция и разгонная характеристика объекта регулирования
Wм(s) =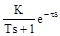 
,
h(t) = K (1 –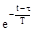 
).1 (t). (3)
Определение параметров модели
Постоянная времени Т определяется как длина подкасательной, проведенной к кривой в точке t = t (рис. 12, а) или в точке перегиба t = tw (рис. 12, б). В этом случае вводится дополнительное запаздывание tд (рис. 12, б), а модель характеризуется эквивалентным запаздыванием.
tэ = t + tд.
Описанный метод является довольно грубым, его можно использовать для предварительной оценки свойств объекта.
Интерполяционный метод Ормана.
Пусть основное запаздывание уже выделено (рис. 10), начало координат смещено в точку t = t. Поребуем, чтобы переходная кривая модели проходила через точки А и В.
Подставляя координаты (tA, DyA) и (tB, DyB) точек А и В и t = tд в формулу (27), для Dy(t) получим систему из двух уравнений:
|
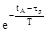) Dх,
DyВ = K (1 –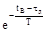 
) Dх.
Решение системы (4) относительно tд и Т имеет вид:
|
,
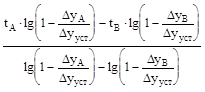Т = –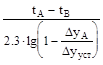 
.
|
tд = 0,5.(3.tА – tВ), Т = 1,25.(tВ – tА).
Для проверки точности модели ординаты экспериментальной кривой в точках t1 = 0,8.Т + tд, t2 = 2.Т + tд сравниваются с соответствующими ординатами переходной кривой модели Dy1 = 0,33. Dyуст, Dy2 = 0,865. Dyуст. Погрешность не должна превышать (0,02 + 0,03. Dyуст).
Выбор типа регулятора
Задача проектировщика состоит в выборе такого типа регулятора, который при минимальной стоимости и максимальной надежности обеспечивал бы заданное качество регулирования. Разработчиком могут быть выбраны релейные, непрерывные или дискретные (цифровые) типы регуляторов.
Выбор типа регулятора обычно начинается с простейших двухпозиционных регуляторов и может заканчиваться самонастраивающимися микропроцессорными регуляторами. Заметим, что по требованиям технологического регламента многие объекты не допускают применения релейного управляющего воздействия.
Рассмотрим показатели качества серийных регуляторов. В качестве серийных предполагаются аналоговые регуляторы, реализующие И, П, ПИ и ПИД – законы управления.
Теоретически, с усложнением закона регулирования качество работы системы улучшается. Известно, что на динамику регулирования наибольшее влияние оказывает величина отношения запаздывания к постоянной времени объекта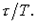 
Эффективность компенсации ступенчатого возмущения регулятором достаточно точно может характеризоваться величиной динамического коэффициента регулирования 
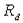, а быстродействие – величиной времени регулирования.
Минимально возможное время регулирования для различных типов регуляторов при оптимальной их настройке определяется таблицей 6.
Таблица 6.
| Закон регулирования | П | ПИ | ПИД |
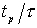
| 6.5 | 12 | 7 |
где –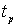 
время регулирования, 
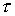– запаздывание в объекте.
Теоретически, в системе с запаздыванием, минимальное время регулирования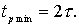 
Руководствуясь таблицей можно утверждать, что наибольшее быстродействие обеспечивает П-закон управления. Однако, если коэффициент усиления П-регулятора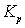 
мал (чаще всего это наблюдается в системах с запаздыванием), то такой регулятор не обеспечивает высокой точности регулирования, т. к. в этом случае велика величина статической ошибки. Если 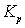имеет величину равную 10 и более, то П-регулятор приемлем, а если 
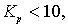то требуется введение в закон управления интегральной составляющей.
Наиболее распространенным на практике является ПИ-регулятор, который обладает следующими достоинствами:
1. Обеспечивает нулевую статическую ошибку регулирования;
2. Достаточно прост в настройке, т. к. настраиваются только два параметра, а именно коэффициент усиления 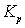и постоянная интегрирования 
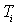. В таком регуляторе имеется возможность оптимизации 
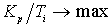, что обеспечивает управление с минимально возможной среднеквадратичной ошибкой регулирования;
3. Малая чувствительность к шумам в канале измерения (в отличии от ПИД-регулятора).
Для наиболее ответственных контуров можно рекомендовать использование ПИД-регулятора, обеспечивающего наиболее высокое быстродействие в системе. Обнако следует учитывать, что это условие выполняется только при его оптимальных настройках (настраиваются три параметра). С увеличением запаздывания в системе резко возрастают отрицательные фазовые сдвиги, что снижает эффект действия дифференциальной составляющей регулятора. Поэтому качество работы ПИД-регулятора для систем с большим запаздыванием становится сравнимо с качеством работы ПИ-регулятора. Кроме этого, наличие шумов в канале измерения в системе с ПИД-регулятором приводит к значительным случайным колебаниям управляющего сигнала регулятора, что увеличивает дисперсию ошибки регулирования и износ исполнительного механизма. Таким образом, ПИД-регулятор следует выбирать для систем регулирования, с относительно малым уровнем шумов и величиной запаздывания в объекте управления. Примерами таких систем является системы регулирования температуры.
При выборе типа регулятора рекомендуется ориентироваться на величину отношения запаздывания к постоянной времени в объекте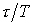 
. Если 
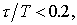то можно выбрать релейный, непрерывный или цифровой регуляторы. Если 
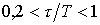, то должен быть выбран непрерывный или цифровой, ПИ- или ПИД-регулятор. Если 
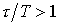, то выбирают специальный цифровой регулятор с упредителем, который компенсирует запаздывание в контуре управления. Однако этот же регулятор рекомендуется применять и при меньших отношениях .
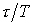6.3 Формульный метод определения настроек регулятора
Метод используется для быстрой, приближенной оценки значений параметров настройки регулятора для трех видов оптимальных типовых процессов регулирования.
Метод применим как для статических объектов с самовыравниванием (таблица 2.2), так и для объектов без самовыравнивания (таблица 2.3).
Таблица 5.
| Регулятор | Типовой процесс регулирования | ||
| апериодический | с 20% перерегулированием |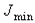 
| |
| И |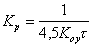 
| 
|
|
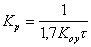
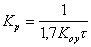
| П |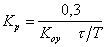 
| 
| 
|
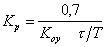
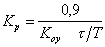
| ПИ |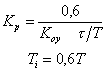 
| 
| 
|
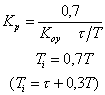
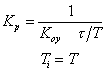
| ПИД |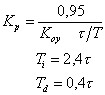 
| 
| 
|
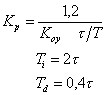
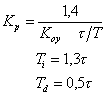
где T, ,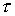 
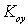– постоянная времени, запаздывание и коэффициент усиления объекта.
В этих формулах предполагается, что настраивается регулятор с зависимыми настройками, передаточная функция которого имеет вид:
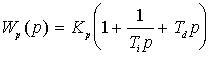, (6)
где – 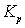коэффициент усиления регулятора, 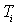– время изодрома (постоянная интегрирования регулятора), 
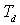– время предварения (постоянная дифференцирования).
Таблица 6.
| Регулятор | Типовой процесс регулирования | ||
| апериодический | с 20% перерегулированием |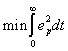 
| |
| П |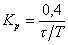 
| 
| - |
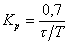
| ПИ |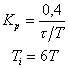 
| 
| 
|
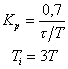
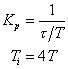
| ПИД |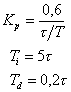 
| 
| 
|
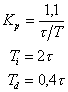
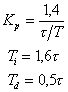
Дата: 2019-12-10, просмотров: 313.
