1) Если a + b + c = 0 в уравнении ax² + bx + c = 0, то
х1=1, а х2 =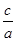 
.
Доказательство:
В уравнении ax² + bx + c = 0, его корни
x1,2 =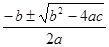 
(1).
Представим b из равенства a + b + c = 0
Подставим это выражение в формулу (1):
х1,2=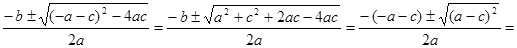 
= 
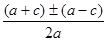
Если рассмотрим по отдельности два корня уравнения, получим:
1) х1=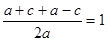 
2) х2=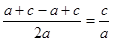 
Отсюда следует: х1=1, а х2 = .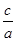
1. Пример:
2х² - 3х + 1 = 0
a = 2, b = -3, c = 1.
a + b + c = 0, следовательно
х1 = 1
х2 = ½
2. Пример:
418х² - 1254х + 836 = 0
Этот пример очень тяжело решить через дискриминант, но, зная выше приведенную формулу его с легкостью можно решить.
a = 418, b = -1254, c = 836.
х1 = 1 х2 = 2
2) Если a - b + c = 0, в уравнении ax² + bx + c = 0, то:
х1=-1, а х2 =- .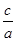
Доказательство:
Рассмотрим уравнение ax² + bx + c = 0, из него следует, что:
x1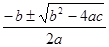,2 = 
(2).
Представим b из равенства a - b + c = 0
b = a + c, подставим в формулу (2):
x1,2=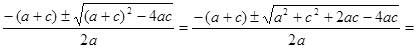 
= 
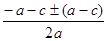
Получаем два выражения:
1) х1=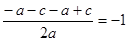 
2) х2=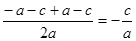 
Эта формула похожа на предыдущую, но она тоже важна, т.к. часто встречаются примеры такого типа.
1) Пример:
2х² + 3х + 1 = 0
a = 2, b = 3, c = 1.
a - b + c = 0, следовательно
х1 = -1
х2 = -1/2
2) Пример:
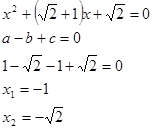
Ответ: x1 = -1; х2 = - 
3) Метод “переброски”
Корни квадратных уравнений y² + by + аc = 0 и ax² + bx + c = 0 связанны соотношениями:
х1 =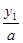 
и х2 =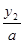 
Доказательство:
а) Рассмотрим уравнение ax² + bx + c = 0
x1,2 = =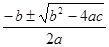 
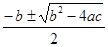
б) Рассмотрим уравнение y² + by + аc = 0
y1,2 = 
Заметим, что дискриминанты у обоих решений равны, сравним корни этих двух уравнений. Они отличаются друг от друга на старший коэффициент, корни первого уравнения меньше корней второго на а. Используя теорему Виета и выше приведенное правило, нетрудно решать разнообразные уравнения.
Пример:
Имеем произвольное квадратное уравнение
10х² - 11х + 3 = 0
Преобразуем это уравнение по приведенному правилу
y² - 11y + 30 = 0
Получим приведенное квадратное уравнение, которое можно достаточно легко решить с помощью теоремы Виета.
Пусть y1 и y2 корни уравнения y² - 11y + 30 = 0
y1y2 = 30 y1 = 6
y1 + y2 = 11 y2 = 5
Зная, что корни этих уравнений отличны друг от друга на а, то
х1 = 6/10 = 0,6
х2 = 5/10 = 0,5
В некоторых случаях удобно решать сначала не данное уравнение ax² + bx + c = 0, а приведенное y² + by + аc = 0, которое получается из данного «переброской» коэффициента а, а затем разделить найденный корни на а для нахождения исходного уравнения.
2.5 Формула Виета для многочленов (уравнений) высших степеней
Формулы, выведенные Виетом для квадратных уравнений, верны и для многочленов высших степеней.
Пусть многочлен
P(x) = a0xn + a1xn-1 + … +an
Имеет n различных корней x1 , x2 …, xn.
В этом случае он имеет разложение на множители вида:
a0xn + a1xn-1 +…+ an = a0( x – x1)( x – x2)…(x – xn)
Разделим обе части этого равенства на a0 ≠ 0 и раскроем в первой части скобки. Получим равенство:
xn + (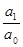 
)xn-1 + … + ( 
) = xn – (x1 + x2 + … + xn) xn-1 + ( x1x2 + x2x3 + … + xn-1xn)xn-2 + … +(-1)n x1x2 … xn
Но два многочлена тождественно равны в том и только в том случае, когда коэффициенты при одинаковых степенях равны. Отсюда следует, что выполняется равенство
x1 + x2 + … + xn = -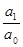
x1x2 + x2x3 + … + xn-1xn =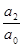 
x1x2 … xn = (-1)n
Например, для многочленов третей степени
a0x³ + a1x² + a2x + a3
Имеем тождества
x1 + x2 + x3 = -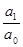 
x1x2 + x1x3 + x2x3 =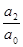 
x1x2x3 = -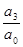 
Как и для квадратных уравнений, эту формулу называют формулами Виета. Левые части этих формул являются симметрическими многочленами от корней x1 , x2 …, xn данного уравнения, а правые части выражаются через коэффициент многочлена.
Дата: 2019-12-10, просмотров: 262.
