Квадратные уравнения и уравнения высших порядков
Выполнили:
Ученики 8 "Б" класса
Кузнецов Евгений и Руди Алексей
Руководитель:
Зенина Алевтина Дмитриевна
преподаватель математики
Тюмень
2005
Оглавление
Введение
Глава 1. История квадратных уравнений и уравнений высших порядков
1.1 Уравнения в Древнем Вавилоне
1.2 Уравнения арабов
1.3 Уравнения в Индии
Глава 2. Теория квадратные уравнения и уравнения высших порядков
2.1 Основные понятия
2.2 Формулы четного коэффициента при х
2.3 Теорема Виета
2.4 Квадратные уравнения частного характера
2.5 Теорема Виета для многочленов (уравнений) высших степеней
2.6 Уравнения, сводимые к квадратным (биквадратные)
2.7 Исследование биквадратных уравнений
2.8 Формулы Кордано
2.9 Симметричные уравнения третьей степени
2.10 Возвратные уравнения
Схема Горнера
Заключение
Список используемой литературы
Приложение 1
Приложение 2
Приложение 3
Введение
Уравнения в школьном курсе алгебры занимают ведущее место. На их изучение отводится времени больше, чем на любую другую тему. Действительно, уравнения не только имеют важное теоретическое значение, но и служат чисто практическим целям. Подавляющее число задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений. Овладевая способами их решения, мы находим ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство, промышленность, связь и т. д.).
В этом реферате хотелось бы отобразить формулы и способы решения различных уравнений. Для этого приводятся уравнения, которые не изучаются в школьной программе. В основном это уравнения частного характера и уравнения высших степеней. Чтобы раскрыть эту тему приводятся доказательства этих формул.
Задачи нашего реферата:
- улучшить навыки решения уравнений
- наработать новые способы решения уравнений
- выучить некоторые новые способы и формулы для решения этих уравнений.
Объект исследования - элементарная алгебра Предмет исследования уравнения. Выбор этой темы основывался на том, что уравнения есть как в программе начальной, так и в каждом последующем классе общеобразовательных школ, лицеев, колледжей. Многие геометрические задачи, задачи по физике, химии и биологии решаются с помощью уравнений. Уравнения решали двадцать пять веков назад. Они создаются и сегодня – как для использования в учебном процессе, так и для конкурсных экзаменов в вузы, для олимпиад самого высокого уровня.
Глава 1. История квадратных уравнений и уравнений высших порядков
Уравнения арабов
Некоторые способы решения уравнений как квадратных, так и уравнений высших степеней были выведены арабами. Так известный арабский математик Ал-Хорезми в своей книге «Ал - джабар» описал многие способы решения различных уравнений. Их особенность была в том, что Ал-Хорезми применял сложные радикалы для нахождения корней (решений) уравнений. Необходимость в решении таких уравнений была нужна в вопросах о разделе наследства.
Уравнения в Индии
Квадратные уравнения решали и в Индии. Задачи на квадратные уравнения встречаются уже в астрономическом трактате «Ариабхаттиам», составленном в 499 году индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта (VII век), изложил общее правило решения квадратных уравнений, приведенных к единой конической форме:
aх² + bx = c, где a > 0
В этом уравнении коэффициенты, кроме а, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.
В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи ». Задачи часто облекались в стихотворную форму.
Различные уравнения как квадратные, так и уравнения высших степеней решались нашими далекими предками. Эти уравнения решали в самых разных и отдаленных друг от друга странах. Потребность в уравнениях была велика. Уравнения применялись в строительстве, в военных делах, и в бытовых ситуациях.
Основные понятия
Квадратным уравнением называют уравнения вида
ax²+bx+c = 0,
где коэффициенты a, b, c – любые действительные числа, причём a ≠ 0.
Квадратное уравнение называют приведённым, если его старший коэффициент равен 1.
Пример:
x2 + 2x + 6 = 0.
Квадратное уравнение называют не приведенным, если старший коэффициент отличен от 1.
Пример:
2x2 + 8x + 3 = 0.
Полное квадратное уравнение - квадратное уравнение, в котором присутствуют все три слагаемых, иными словами, это уравнение, у которого коэффициенты b и c отличны от нуля.
Пример:
3x2 + 4x + 2 = 0.
Неполное квадратное уравнение – это квадратное уравнение, у которого хотя бы один коэффициент b, c равен нулю.
Таким образом, выделяют три вида неполных квадратных уравнений:
1) ax² = 0 (имеет два совпадающих корня x = 0).
2) ax² + bx = 0 (имеет два корня x1 = 0 и x2 = - 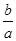 )
)
Пример:
x2 + 5x = 0
x(x+5) =0
x1= 0, x2 = -5.
Ответ: x1=0, x2= -5.
3) ax² + c = 0
Если – 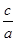 <0 - уравнение не имеет корней.
<0 - уравнение не имеет корней.
Пример:
5x2 + 6 = 0
Ответ: уравнение не имеет корней.
Если – 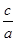 > 0, то x1,2 = ±
> 0, то x1,2 = ± 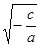
Пример:
2x2 – 6 = 0
х2=± 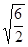
х1,2=± 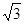
Ответ: х1,2=± 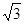
Любое квадратное уравнение можно решить через дискриминант (b² - 4ac). Обычно выражение b² - 4ac обозначают буквой D и называют дискриминантом квадратного уравнение ax² +bx + c = 0 (или дискриминантом квадратного трёх члена ax² + bx + c)
Пример:
х2 +14x – 23 = 0
D = b2 – 4ac = 144 + 92 = 256
x1,2 = 
x1 = 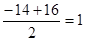
x2 = 
Ответ: x1 = 1, x2 = - 15.
В зависимости от дискриминанта уравнение может иметь или не иметь решение.
1) Если D < 0, то не имеет решения.
2) Если D = 0, то уравнение имеет два совпадающих решения x1,2 = 
3) Если D > 0, то имеет два решения, находящиеся по формуле:
x1,2 = 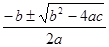
Теорема Виета
Очень любопытное свойство корней квадратного уравнения обнаружил французский математик Франсуа Виет. Это свойство назвали теорема Виета:
Чтобы числа x1 и x2 являлись корнями уравнения:
ax² + bx + c = 0
необходимо и достаточно выполнения равенства
x1 + x2 = -b/a и x1x2 = c/a
Теорема Виета позволяет судить о знаках и абсолютной величине квадратного уравнения
А именно
x² + bx + c = 0
1. Если b>0, c>0 то оба корня отрицательны.
2. Если b<0, c>0 то оба корня положительны.
3. Если b>0, c<0 то уравнение имеет корни разных знаков, причём отрицательный корень по абсолютной величине больше положительного.
4. Если b<0, c<0 то уравнение имеет корни разных знаков, причём отрицательный корень по абсолютной величине меньше положительного.
Имеем тождества
x1 + x2 + x3 = - 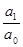
x1x2 + x1x3 + x2x3 = 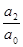
x1x2x3 = - 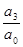
Как и для квадратных уравнений, эту формулу называют формулами Виета. Левые части этих формул являются симметрическими многочленами от корней x1 , x2 …, xn данного уравнения, а правые части выражаются через коэффициент многочлена.
Формула Кардано
Если воспользоваться современной символикой, то вывод формулы Кардано может иметь такой вид:
х = 
Эта формула определяет корни общего уравнения третей степени:
ax3 + 3bx2 + 3cx + d = 0.
Эта формула очень громоздкая и сложная (она содержит несколько сложныных радикалов). Она не всегда примениться, т.к. очень сложна для заполнения.
Возвратные уравнения
Возвратное уравнение – алгебраическое уравнение
а0хn + a1xn – 1 + … + an – 1x + an =0,
в котором ак = an – k, где k = 0, 1, 2 …n, причем, а ≠ 0.
Задачу нахождения корней возвратного уравнения сводят к задаче нахождения решений алгебраического уравнения меньшей степени. Термин возвратные уравнения был введён Л. Эйлером.
Уравнение четвёртой степени вида:
ax4 + bx3 + cx2 + bmx + am² = 0, (a ≠ 0).
Приведя это уравнение к виду
a (x² + m²/x²) + b(x + m/x) + c = 0, и y = x + m/x и y² - 2m = x² + m²/x²,
откуда уравнение приводится к квадратному
ay² + by + (c-2am) = 0.
Пример:
3х4 + 5х3 – 14х2 – 10х + 12 = 0
Разделив его на х2, получим эквивалентное уравнение
3х2 + 5х – 14 – 5 ×  , или
, или
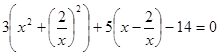
Где 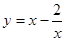 и
и 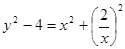
3(y2 - 4) + 5y – 14 = 0, откуда
y1 = 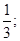 y2 = -2, следовательно
y2 = -2, следовательно
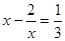 и
и 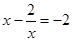 , откуда
, откуда
х1,2 = 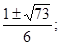
х3,4 = 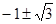
Ответ: х1,2 = 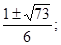 х3,4 =
х3,4 = 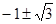 .
.
Частным случаем возвратных уравнений являются симметричные уравнения. О симметричных уравнениях третей степени мы говорили ранее, но существуют симметричные уравнения четвертой степени.
Симметричные уравнения четвертой степени.
1) Если m = 1, то это симметричное уравнение первого рода, имеющее вид
ax4 + bx3 + cx2 + bx + a = 0 и решающееся новой подстановкой
y = 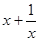
2) Если m = -1, то это симметричное уравнение второго рода, имеющее вид
ax4 + bx3 + cx2 - bx + a = 0 и решающееся новой подстановкой
y = 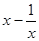
Схема Горнера
Для деления многочленов применяется правило “деления углом”, или схема Горнера. С этой целью располагают многочлены по убывающим степеням х и находят старший член частного Q(x) из условия, что при умножении его на старший член делителя D(x) получается старший член делимого P(x). Найденный член частного умножают, затем на делитель и вычитают из делимого. Старший член частного определяют из условия, что он при умножении на старший член делителя даёт старший член многочлена разности и т.д. Процесс продолжается до тех пор, пока степень разности не окажется меньше степени делителя.(см. приложение №2).
В случае уравнений R = 0 этот алгоритм заменяется схемой Горнера.
Пример:
х3 + 4х2 + х – 6 = 0
Находим делители свободного члена ±1; ± 2; ± 3; ± 6.
Левую часть уравнения обозначим f(x). Очевидно, что f(1) = 0, x1 = 1. Делим f(x) на х – 1. (см. приложение №3)
Значит,
х3 + 4х2 + х – 6 = (х – 1) (х2 + 5х + 6)
Последний множитель обозначим через Q(x). Решаем уравнение Q(x) = 0.
х2,3 = 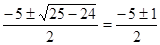
Ответ: 1; -2; -3.
В этой главе мы привели некоторые формулы решения различных уравнений. Большинство этих формул решения уравнений частного характера. Эти свойства очень удобны так, как гораздо легче решать уравнения по отдельной формуле для этого уравнения, а не по общему принципу. К каждому из способов мы привели доказательство и несколько примеров.
Заключение
В первой главе была рассмотрена история возникновения квадратных уравнений и уравнений высших порядков. Различные уравнения решали более 25 веков назад. Множество способов решения таких уравнений были созданы в Вавилоне, Индии. Потребность в уравнениях была и будет.
Во второй главе приведены различные способы решения (нахождения корней) квадратных уравнений и уравнений высших порядков. В основном это способы решения для уравнений частного характера, то есть к каждой группе уравнений, объединенных какими- либо общими свойствами или видом, приведено особое правило, которое применяется только для этой группы уравнений. Этот способ (подбора к каждому уравнению собственной формулы) гораздо легче, чем нахождение корней через дискриминант.
В этом реферате достигнуты все цели и выполнены основные задачи, доказаны и разучены новые, ранее неизвестные формулы. Мы проработали много вариантов примеров перед тем, как занести их в реферат, по этому мы уже представляем, как решать некоторые уравнения. Каждое решение пригодится нам в дальнейшей учебе. Этот реферат помог классифицировать старые знания и познать новые.
Список литературы
1. Виленкин Н.Я. “Алгебра для 8 класса”, М., 1995.
2. Галицкий М.Л. “Сборник задач по алгебре”, М. 2002.
3. Даан-Дальмедико Д. “Пути и лабиринты”, М., 1986.
4. Звавич Л.И. “Алгебра 8 класс”, М., 2002.
5. Кушнир И.А. “Уравнения”, Киев 1996.
6. Савин Ю.П. “Энциклопедический словарь юного математика”, М., 1985.
7. Мордкович А.Г. “Алгебра 8 класс”, М., 2003.
8. Худобин А.И. “Сборник задач по алгебре”, М., 1973.
9. Шарыгин И.Ф. “Факультативный курс по алгебре”, М., 1989.
Приложение 1
Исследование биквадратных уравнений
| C | b |
Выводы | ||
| О корнях вспомогательного уравнения ay² +by+c=0 | О корнях данного уравнения a(x²)² +bx² +c=0 | |||
| C < 0 | b- любое действительное число | y < 0 ; y > 0 1 2 | x = ±Öy 1,2 2 | |
| C > 0 | b<0 | D > 0 | y > 0 1,2 | x = ±Öy 1,2,3,4 1,2 |
| D = 0 | y > 0 | x = ±Öy 1,2 . | ||
| D < 0 | Нет корней | Нет корней | ||
| b ≥ 0 | y < 0 1,2 | Нет корней | ||
| Нет корней | Нет корней | |||
| y > 0 ; y < 0 1 2 | x = ±Öy 1,2 1 | |||
| C = 0 | b > 0 | y = 0 | x = 0 | |
| b = 0 | y = 0 | x = 0 | ||
| b < 0 | y = 0 | x = 0 | ||
Приложение 2
Деление многочлена на многочлен «уголком»
| A0 | a1 | a2 | ... | an | c | |
| + | ||||||
| b0c | b1c | … | bn-1c | |||
| B0 | b1 | b2 | … | bn | = R (остаток) | |
Приложение 3
Схема Горнера
| Корень | |||||
| 1 | 4 | 1 | -6 | 1 |
| х1 = 1 | |||||
| сносим | 5 | 6 | 0 | ||
 
|  1 1
|  1×1 +4 = 5 1×1 +4 = 5
| 5×1 + 1 = 6 | 6×1 – 6 = 0 | |
| корень | |||||
| х1 = 1 |
Квадратные уравнения и уравнения высших порядков
Выполнили:
Ученики 8 "Б" класса
Кузнецов Евгений и Руди Алексей
Руководитель:
Зенина Алевтина Дмитриевна
преподаватель математики
Тюмень
2005
Оглавление
Введение
Глава 1. История квадратных уравнений и уравнений высших порядков
1.1 Уравнения в Древнем Вавилоне
1.2 Уравнения арабов
1.3 Уравнения в Индии
Глава 2. Теория квадратные уравнения и уравнения высших порядков
2.1 Основные понятия
2.2 Формулы четного коэффициента при х
2.3 Теорема Виета
2.4 Квадратные уравнения частного характера
2.5 Теорема Виета для многочленов (уравнений) высших степеней
2.6 Уравнения, сводимые к квадратным (биквадратные)
2.7 Исследование биквадратных уравнений
2.8 Формулы Кордано
2.9 Симметричные уравнения третьей степени
2.10 Возвратные уравнения
Схема Горнера
Заключение
Список используемой литературы
Приложение 1
Приложение 2
Приложение 3
Введение
Уравнения в школьном курсе алгебры занимают ведущее место. На их изучение отводится времени больше, чем на любую другую тему. Действительно, уравнения не только имеют важное теоретическое значение, но и служат чисто практическим целям. Подавляющее число задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений. Овладевая способами их решения, мы находим ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство, промышленность, связь и т. д.).
В этом реферате хотелось бы отобразить формулы и способы решения различных уравнений. Для этого приводятся уравнения, которые не изучаются в школьной программе. В основном это уравнения частного характера и уравнения высших степеней. Чтобы раскрыть эту тему приводятся доказательства этих формул.
Задачи нашего реферата:
- улучшить навыки решения уравнений
- наработать новые способы решения уравнений
- выучить некоторые новые способы и формулы для решения этих уравнений.
Объект исследования - элементарная алгебра Предмет исследования уравнения. Выбор этой темы основывался на том, что уравнения есть как в программе начальной, так и в каждом последующем классе общеобразовательных школ, лицеев, колледжей. Многие геометрические задачи, задачи по физике, химии и биологии решаются с помощью уравнений. Уравнения решали двадцать пять веков назад. Они создаются и сегодня – как для использования в учебном процессе, так и для конкурсных экзаменов в вузы, для олимпиад самого высокого уровня.
Глава 1. История квадратных уравнений и уравнений высших порядков
Дата: 2019-12-10, просмотров: 346.