Рассмотрим пример. Предположим, что очередь содержит три элемента - в позициях 3, 4 и 5 пятиэлементного массива. Хотя массив и не заполнен, последний элемент очереди занят.
Если теперь делается попытка поместить в очередь элемент G, то он будет записан в первую позицию массива, как это показано на рис. 2.17. Первый элемент очереди есть Q(3), за которым следуют элементы Q (4), Q(5) и Q(l).
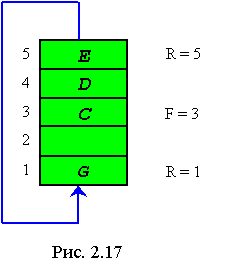
К сожалению, при таком представлении довольно трудно определить, когда очередь пуста. Условие R<F больше не годится для такой проверки, поскольку на рис. 2. 17 показан случай, при котором данное условие выполняется, но очередь при этом не является пустой.
Одним из способов решения этой проблемы является введение соглашения, при котором значение F есть индекс элемента массива, немедленно предшествующего первому элементу очереди, а не индексу самого первого элемента. В этом случае, поскольку R содержит индекс последнего элемента очереди, условие F = R подразумевает, что очередь пуста.
Отметим, что перед началом работы с очередью, в F и R устанавливается значение последнего индекса массива maxQ, а не 1 и 0, поскольку при таком представлении очереди последний элемент массива немедленно предшествует первому элементу. Поскольку R = F, то очередь изначально пуста.

Рис. 2.17’
Основные операции с кольцевой очередью:
1. Вставка элемента q в очередь x.
Insert(q,x)
2. Извлечение элемента из очереди x.
Remove(q)
3. Проверка очереди на пустоту.
Empty(q)
4.Проверка очереди на переполнение
Full(q).
Алгоритм проверки на пустоту кольцевой очереди следующий:
Empty(q)
if F = R
then empty = true
else empty = false
endif
return
Алгоритм извлечения элемента из кольцевой очереди следующий:
Remove(q)
empty (q)
if empty = true
then “ пусто ”
stop
endif
if F = maxQ
then F =1
else F = F+1
endif
x = q ( F )
return
Отметим, что значение F должно быть модифицировано до момента извлечения элемента.
Переполнение очереди происходит в том случае, если весь массив уже занят элементами очереди, и при этом делается попытка разместить в ней еще один элемент.
Для того чтобы запрограммировать операцию вставки, должна быть проанализирована ситуация, при которой возникает переполнение. Переполнение происходит в том случае, если весь массив уже занят элементами очереди и при этом делается попытка разместить в ней еще один элемент. Рассмотрим, например, очередь на рис. 2. 17. В ней находятся три элемента — С, D и Е, соответственно расположенные в Q (3), Q (4) и Q (5). Поскольку последний элемент в очереди занимает позицию Q (5), значение R равно 5. Так как первый элемент в очереди находится в Q (3), значение F равно 2. На рис. 2. 17 в очередь помещается элемент G, что приводит к соответствующему изменению значения R. Если произвести следующую вставку, то массив становится целиком заполненным, и попытка произвести еще одну вставку приводит к переполнению. Это регистрируется тем фактом, что F = R, а это как раз и указывает на переполнение. Очевидно, что при такой реализации нет возможности сделать различие между пустой и заполненной очередью.
Одно из решений состоит в том, чтобы пожертвовать одним элементом массива и позволить очереди расти до объема на единицу меньшего максимального. Рисунок 2.17’’ иллюстрирует данное соглашения при реализации очереди с помощью массива из 5 элементов.

Рис. 2.17’’
Если, например, очередь реализуется на массиве из 100 элементов, то очередь может содержать до 99 элементов. Попытка разместить в очереди 100-й элемент приведет к переполнению.
Проверка на переполнение в подпрограмме insert производится после установления нового значения для R, в то время как проверка на потерю значимости в подпрограмме remove производится сразу же после входа в подпрограмму до момента обновления значения F.
Алгоритм операции вставки элемента в кольцевую очередь при такой реализации следующий:
Insert(q,x)
if R = maxQ
then R = 1
else R = R+1
endif
‘проверка на переполнение’
if R = F
then print «переполнение очереди»
stop
endif
q (R) =x
return
Дек
От английского DEQ - Double Ended Queue (Очередь с двумя концами)
Особенностью деков является то, что запись и считывание элементов может производиться с двух концов (рис. 2.18).

Дек можно рассматривать и в виде двух стеков, соединенных нижними границами. Возьмем пример, иллюстрирующий принцип построения дека. Рассмотрим состав на железнодорожной станции. Новые вагоны к составу можно добавлять либо к его концу, либо к началу. Аналогично, чтобы отсоединить от состава вагон, находящийся в середине, нужно сначала отсоединить все вагоны или вначале, или в конце состава, отсоединить нужный вагон, а затем присоединить их снова.
Операции над деками:
1. Insert - вставка элемента.
2. Remove - извлечение элемента из дека.
3. Empty - проверка на пустоту.
4. Full - проверка на переполнениe.
Контрольные вопросы
1. Что такое структуры данных?
2. Назовите уровни представления данных?
3. Какова классификация структур данных?
4. Какая статическая структура является самой простой?
5. Перечислите основные элементы таблицы.
6. Назовите их основные особенности.
7. Что такое вектор?
8. Что представляет из себя запись?
9. Какова структура записи?
10. К каким структурам данных относятся очереди и стеки?
11. Каково правило выборки элемента из стека?
12. Какая операция читает верхний элемент стека без его удаления?
13. Какую дисциплину обслуживания принято называть FIFO, а какую - LIFO?
14. Признак заполнения кольцевой очереди?
15. Признак пустой очереди?
16. Что называется списком?
17. Перечислите виды списков.
18. Назовите элементы очереди.
19. Как организуется кольцевая очередь?
20. Какова особенность деков?
Дата: 2019-12-10, просмотров: 386.