Для работы с очередью вводят два указателя: один – на начало очереди (F), второй – на ее конец (R).
Full (q)
if R = maxQ then full = true
else full = false
endif
return
Empty (q)
if R < F then empty = true
else empty = false
endif
return
Insert (q, x)
Full (q)
if full = true then ‘ переполнение ’
stop
return
endif
R = R + 1
q(R) = x
return
Remove (q)
Empty (q)
if empty = true then ‘ пусто ’
stop
return
endif
x = q(F)
F = F + 1
return
Пример работы с очередью с использованием стандартных процедур.
Пусть очередь реализуется с помощью массива из 5 элементов.
MaxQ = 5
R = 0, F = 1
Условие пустоты очереди R < F (0 < 1)
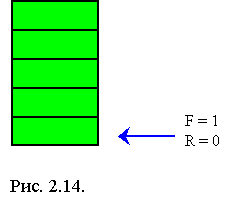
Производим вставку элементов A, B и C в очередь.
Insert(q, A);
Insert(q, B);
Insert(q, C);
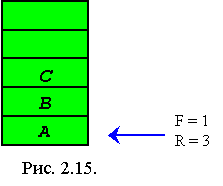
Убираем элементы A и B из очереди.
Remove(q);
Remove(q);
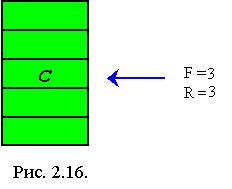
Добавляем элементы D и E:
Insert (q, D);
Insert (q, E);
Убираем элементы С,D и E из очереди:
Remove (q);
Remove (q);
Remove (q).
К сожалению, при подобном представлении очереди возникла абсурдная ситуация, при которой очередь является пустой, однако новый элемент разместить в ней нельзя, так как R = maxQ.
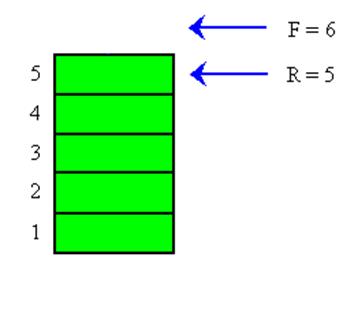
Рис. 2.16 `
Одним из решений возникшей проблемы может быть модификация операции remove таким образом, что при удалении очередного элемента вся очередь смещается к началу массива.
Переменная F больше не требуется, поскольку первый элемент массива всегда является началом очереди.
Пустая очередь представлена очередью, для которой значение R равно нулю.
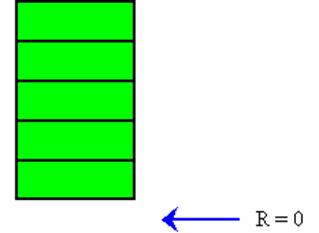
Рис. 2.16’’
Произведем вставку элементов A, B и C в очередь:
Insert (q, A);
Insert (q, B);
Insert (q, C);
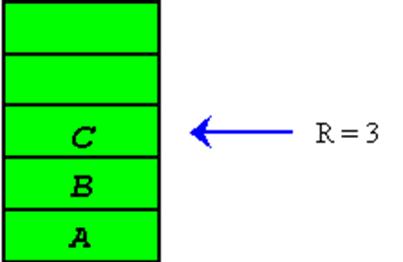
Рис. 2.16’’’
Убираем элемент A из очереди:
Remove (q)
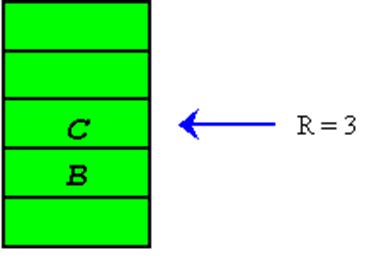
Рис. 2.16’’’’
Операция remove (q) может быть в этом случае реализована следующим образом:
Remove (q)
x = q(1)
for i =1 to R-1
q(i) = q(i+1)
next i
R =R-1
return
При такой модификации элементы очереди смещаются к началу массива, R=2.
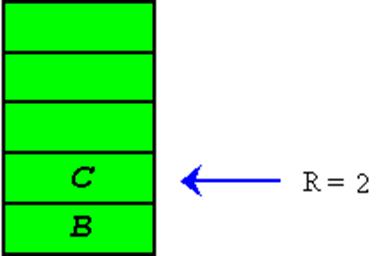
Рис 2.16’’’’’.
Однако этот метод весьма непроизводителен. Каждое удаление требует перемещения всех оставшихся в очереди элементов. Если очередь содержит 500 или 1000 элементов, то очевидно, что это весьма неэффективный способ. Кроме того, операция удаления элемента из очереди логически предполагает манипулирование только с одним элементом, т. е. с тем, который расположен в начале очереди. Реализация данной операции должна отражать именно этот факт, не производя при этом множества дополнительных действий.
Другой способ предполагает рассматривать массив, который содержит очередь в виде замкнутого кольца, а не линейной последовательности, имеющей начало и конец. Это означает, что первый элемент очереди следует сразу же за последним. Это означает, что даже в том случае, если последний элемент занят, новое значение может быть размещено сразу же за ним на месте первого элемента, если этот первый элемент пуст.
Дата: 2019-12-10, просмотров: 354.