Большинство современных потребителей электрической энергии имеют индуктивный характер нагрузки, токи которой отстают по фазе от напряжения источника. Активная мощность таких потребителей при
заданных значениях тока и напряжения зависит от cosφ
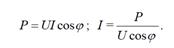
Следовательно, повышение коэффициента мощности приводит к уменьшению тока.
Если обозначить сопротивление проводов линии, то потери мощности в ней можно определить так: Rл
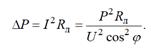
Таким образом, чем выше cosφ потребителя, тем меньше потери мощности в линии и дешевле передача электроэнергии. Коэффициент мощности показывает, как используется номинальная мощность источника.
Низкий cos φ приводит к: потерям мощности в сети; повышению потерь трансформатора; отклонению напряжения сети от номинала; дополнительным затратам на сооружение более мощных электростанций.
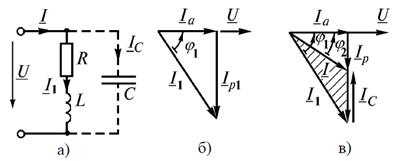
Из векторной диаграммы видно, что φ2<φ1, т.е. после включения конденсатора коэффициент мощности повышается от cosφ1 до cosφ2. Емкость конденсатора можно рассчитать при помощи векторной диаграммы токов
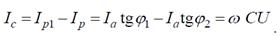
Учитывая, что 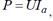 запишем емкость конденсатора
запишем емкость конденсатора 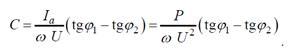
На практике обычно коэффициент мощности повышают не до 1,0, а до 0,90...0,95, так как полная компенсация требует дополнительной установки конденсаторов, что часто экономически не оправдано. Предприятия стремятся оплатить льготный тариф за электрическую энергию, для повышения cosφ существуют естественный и искусственный пути. Естественные пути: 1)Эксплуатировать силовые установки (двигатели, трансформаторы и другие) в номинальном режиме, которые используют максимум КПД и минимальные потери мощности. 2)Исключать режимы работ асинхронных двигателей и трансформаторов в холостом ходе, при которых cosφ=0,17. Искусственные пути: 1)Для повышения cosφ реальных установок применяют параллельное включение конденсаторов различных параллельных обмоток 2)Использование специальной машины, которая получила название асинхронного конденсатора.
Активная, реактивная и полная мощности цепи однофазного синусоидального тока.
Формулы для определения полной, активной и реактивной мощностей цепи однофазного синусоидального тока: 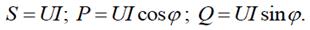 Рассмотрим простой прием, позволяющий найти активную и реактивную мощности по комплексным напряжению и току. Для этого умножим комплекс напряжения на сопряженный комплекс тока
Рассмотрим простой прием, позволяющий найти активную и реактивную мощности по комплексным напряжению и току. Для этого умножим комплекс напряжения на сопряженный комплекс тока 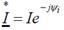 :
:
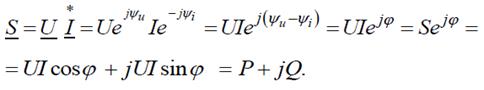
Полученное значение S называют комплексом полной мощности. Вещественная часть комплексной мощности равна активной мощности, мнимая часть – реактивной: 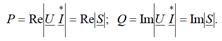
Дата: 2019-12-10, просмотров: 402.