Идеальные и реальные источники э.д.с. и тока, их вольтамперные характеристики.

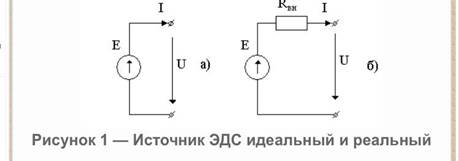
    Источник ЭДС это активный элемент цепи, который имеет два вывода. Напряжение на этих выводах не зависит от сопротивления цепи, в которую он включен. То есть независимо от того какой ток будет создавать источник ЭДС в цепи напряжение на его выводах не изменится. Считается, что внутри источника ЭДС отсутствуют пассивные элементы, такие как активное сопротивление, индуктивность и емкость. То есть можно сказать, что внутренне сопротивление источника ЭДС равно нулю.

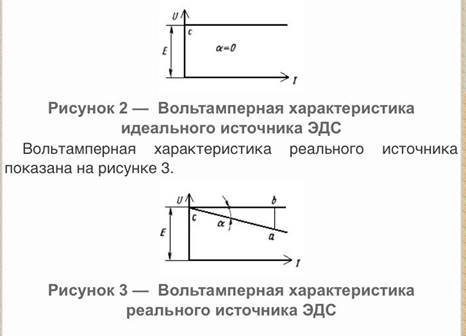
     Идеальный источник ЭДС в природе не существует. И в правду трудно себе представить такой источник. В котором при замыкании его выводов между собой, нулевым сопротивлением, возникнет бесконечно большой ток. Это видно из закона Ома. I=U\R при R=0 получим I=U/0.

   В реальных же источниках ЭДС всегда присутствует внутренне сопротивление. Таким образом, при замыкании выводов между собой падение напряжения на внутреннем сопротивлении уравновешивает ЭДС источника. Следовательно, ток короткого замыкания будет иметь какую-то конечную величину.

У идеального источника тока, величина тока не зависит от величины напряжения на зажимах (рис.2).

I = const .

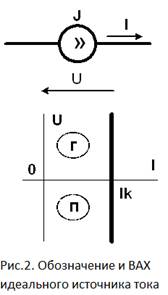Очевидно, что ток короткого замыкания у этого источника всегда равен I_к, а его напряжение холостого хода равно бесконечности (U_хх = ∞). Поскольку ток у идеального источника тока неизменен (ΔI = 0), то он имеет внутреннее сопротивление, равное бесконечности.

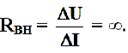
При положительном напряжении и токе источник отдаёт энергию с электрическую цепь и работает в режиме генератора (Г). При обратном направлении напряжения – источник принимает энергию из цепи и работает в режиме приёмника (П).

Применение законов Кирхгофа для расчета линейных электрических цепей постоянного тока.

Последовательное соединение сопротивлений.

3.Взаимные преобразования звезды и треугольника резистивных элементов в линейных электрических цепях постоянного тока.

Расчет линейной электрической цепи постоянного тока методом двух узлов.

Одним из распространенных методов расчета электрических цепей является метод двух узлов. Этот метод применяется в случае, когда в цепи всего два узла.

Алгоритм действий таков:

1 - Потенциал одного из узлов принимается равным нулю

2 - Составляется узловое уравнение для другого узла

3 - Определяется напряжение между узлами

4 - По закону Ома, находятся токи в ветвях

Действующее значение синусоидально изменяющихся электрических величин

Идеальные и реальные источники э.д.с. и тока, их вольтамперные характеристики.

    Источник ЭДС это активный элемент цепи, который имеет два вывода. Напряжение на этих выводах не зависит от сопротивления цепи, в которую он включен. То есть независимо от того какой ток будет создавать источник ЭДС в цепи напряжение на его выводах не изменится. Считается, что внутри источника ЭДС отсутствуют пассивные элементы, такие как активное сопротивление, индуктивность и емкость. То есть можно сказать, что внутренне сопротивление источника ЭДС равно нулю.

     Идеальный источник ЭДС в природе не существует. И в правду трудно себе представить такой источник. В котором при замыкании его выводов между собой, нулевым сопротивлением, возникнет бесконечно большой ток. Это видно из закона Ома. I=U\R при R=0 получим I=U/0.

   В реальных же источниках ЭДС всегда присутствует внутренне сопротивление. Таким образом, при замыкании выводов между собой падение напряжения на внутреннем сопротивлении уравновешивает ЭДС источника. Следовательно, ток короткого замыкания будет иметь какую-то конечную величину.

У идеального источника тока, величина тока не зависит от величины напряжения на зажимах (рис.2).

I = const .

Очевидно, что ток короткого замыкания у этого источника всегда равен I_к, а его напряжение холостого хода равно бесконечности (U_хх = ∞). Поскольку ток у идеального источника тока неизменен (ΔI = 0), то он имеет внутреннее сопротивление, равное бесконечности.

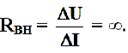
При положительном напряжении и токе источник отдаёт энергию с электрическую цепь и работает в режиме генератора (Г). При обратном направлении напряжения – источник принимает энергию из цепи и работает в режиме приёмника (П).