Этот метод еще не обсчитан на компьютерах.

Запишем на левом крае ещё одно уравнение краевых условий:

M ∙ Y(0) = m .

В качестве строк матрицы M можно взять те краевые условия, то есть выражения тех физических параметров, которые не входят в параметры краевых условий левого края L или линейно независимы с ними. Это вполне возможно, так как у краевых задач столько независимых физических параметров какова размерность задачи, а в параметры краевых условий входит только половина физических параметров задачи. То есть, например, если рассматривается задача об оболочке ракеты, то на левом крае могут быть заданы 4 перемещения. Тогда для матрицы М можно взять параметры сил и моментов, которых тоже 4, так как полная размерность такой задачи – 8. Вектор m правой части неизвестен и его надо найти и тогда можно считать, что краевая задача решена, то есть сведена к задаче Коши, то есть найден вектор Y(0) из выражения:

 ∙ Y(0) = ,

то есть вектор Y(0) находится из решения системы линейных алгебраических уравнений с квадратной невырожденной матрицей коэффициентов, состоящей из блоков U и M.

Аналогично запишем на правом крае ещё одно уравнение краевых условий:

N ∙ Y(0) = n ,

где матрица N записывается из тех же соображений дополнительных линейно независимых параметров на правом крае, а вектор n неизвестен.

Для правого края тоже справедлива соответствующая система уравнений:

 ∙ Y(1) = .

Запишем Y(1) = K(1←0) ∙Y(0) + Y*(1←0)  и подставим в последнюю систему линейных алгебраических уравнений:

 ∙ [ K(1←0) ∙Y(0) + Y*(1←0) ]  = ,

 ∙ K(1←0) ∙Y(0) =  -  ∙ Y*(1←0),

 ∙ K(1←0) ∙Y(0) =  ,

 ∙ K(1←0) ∙Y(0) =  .

Запишем вектор Y(0) через обратную матрицу:

Y(0) =  ∙

и подставим в предыдущую формулу:

 ∙ K(1←0) ∙  ∙  = .

Таким образом, мы получили систему уравнений вида:

В ∙  = ,

где матрица В известна, векторы u и s известны, а векторы m и t неизвестны.

Разобьем матрицу В на естественные для нашего случая 4 блока и получим:

∙  = ,

откуда можем записать, что

В11 ∙ u + B12 ∙ m = s,

B21 ∙ u + B22 ∙ m = t.

Следовательно, искомый вектор m вычисляется по формуле:

m = B12  ∙ (s – B11∙ u).

А искомый вектор n вычисляется через вектор t:

t = B21 ∙ u + B22 ∙ m,

n = t + N ∙ Y*(1←0).

В случае «жестких» дифференциальных уравнений предлагается выполнять поочередное построчное ортонормирование.

Запишем приведенную выше формулу

 ∙ K(1←0) ∙  ∙  =

в виде:

 ∙ K(1←x2) ∙ K(x2←x1) ∙ K(x1←0) ∙  ∙  = .

Эту формулу можно записать в виде разделения левой части на произведение матрицы на вектор:

[  ∙ K(1←x2) ] ∙ { K(x2←x1) ∙ K(x1←0) ∙  ∙  } =

[ матрица  ] ∙ {                вектор                   } = вектор

Эту группу линейных алгебраических уравнений можно подвергнуть построчному ортонормированию, которое сделает строчки [матрицы] ортонормированными, {вектор} затронут не будет, а вектор получит преобразование. То есть получим:

[  ∙ K(1←x2) ] { K(x2←x1) ∙ K(x1←0) ∙  ∙  } =

Здесь следует сказать, что подвектор t подвергать преобразованию не нужно, так как невозможно, так как его первоначальное значение не известно. Но подвектор t нам оказывается и не нужен для решения задачи.

Далее запишем:

[[  ∙ K(1←x2) ]  ∙ K(x2←x1)] { K(x1←0) ∙  ∙  } =

[        матрица               ]     {           вектор       } = вектор

Аналогично и эту группу линейных алгебраических уравнений можно подвергнуть построчному ортонормированию, которое сделает строчки [матрицы] ортонормированными, {вектор} затронут не будет, а вектор получит преобразование. То есть получим:

[[  ∙ K(1←x2) ] 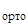K(x2←x1)]  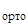{ K(x1←0) ∙  } = .

И так далее.

В результате поочередного ортонормирования получим:

В  ∙  = ,

∙  =  .

Следовательно, искомый вектор m вычисляется по формуле:

m = B12  ∙ (s  – B11 ∙ u).