Метод обсчитан на компьютерах. По нему уже сделано 3 кандидатских физ-мат диссертации.
Метод подходит для любых краевых задач. А для «жестких» краевых задач показано, что метод считает быстрее, чем метод С.К.Годунова до 2-х порядков (в 100 раз), а для некоторых «жестких» краевых задач не требует ортонормирования вовсе. Смотри:
Численный метод переноса краевых условий для жестких дифференциальных уравнений строительной механики
Журнал "ММ", Том: 14 (2002), Номер: 9, 3 стр. 1409-003r.pdf
Полное решение системы дифференциальных уравнений имеет вид
Y(x) = K(x←x 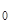 ) ∙ Y(x
) ∙ Y(x 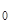 ) + Y*(x←x
) + Y*(x←x 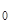 ) .
) .
Или можно записать:
Y(0) = K(0←x  ) ∙ Y(x
) ∙ Y(x  ) + Y*(0←x
) + Y*(0←x  ) .
) .
Подставляем это выражение для Y(0) в краевые условия левого края и получаем:
U∙Y(0) = u,
U∙[ K(0←x  ) ∙ Y(x
) ∙ Y(x  ) + Y*(0←x
) + Y*(0←x  ) ] = u,
) ] = u,
[ U∙ K(0←x  ) ] ∙ Y(x
) ] ∙ Y(x  ) = u - U∙Y*(0←x
) = u - U∙Y*(0←x  ) .
) .
Или получаем краевые условия, перенесенные в точку x  :
:
U  ∙ Y(x
∙ Y(x  ) = u
) = u  ,
,
где U  = [ U∙ K(0←x
= [ U∙ K(0←x  ) ] и u
) ] и u  = u - U∙Y*(0←x
= u - U∙Y*(0←x  ) .
) .
Далее запишем аналогично
Y(x  ) = K(x
) = K(x  ←x
←x  ) ∙ Y(x
) ∙ Y(x  ) + Y*(x
) + Y*(x  ←x
←x  )
)
И подставим это выражение для Y(x  ) в перенесенные краевые условия точки x
) в перенесенные краевые условия точки x 
U  ∙ Y(x
∙ Y(x  ) = u
) = u  ,
,
U  ∙ [ K(x
∙ [ K(x  ←x
←x  ) ∙ Y(x
) ∙ Y(x  ) + Y*(x
) + Y*(x  ←x
←x  ) ] = u
) ] = u  ,
,
[ U  ∙ K(x
∙ K(x  ←x
←x  ) ] ∙ Y(x
) ] ∙ Y(x  ) = u
) = u  - U
- U  ∙ Y*(x
∙ Y*(x  ←x
←x  ) ,
) ,
Или получаем краевые условия, перенесенные в точку x  :
:
U  ∙ Y(x
∙ Y(x  ) = u
) = u  ,
,
где U  = [ U
= [ U  ∙ K(x
∙ K(x  ←x
←x  ) ] и u
) ] и u  = u
= u  - U
- U  ∙ Y*(x
∙ Y*(x  ←x
←x  ) .
) .
И так в точку x 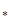 переносим матричное краевое условие с левого края и таким же образом переносим матричное краевое условие с правого края и получаем:
переносим матричное краевое условие с левого края и таким же образом переносим матричное краевое условие с правого края и получаем:
U 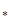 ∙ Y(x
∙ Y(x 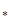 ) = u
) = u 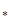 ,
,
V 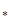 ∙ Y(x
∙ Y(x 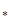 ) = v
) = v 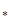 .
.
Из этих двух матричных уравнений с прямоугольными горизонтальными матрицами коэффициентов очевидно получаем одну систему линейных алгебраических уравнений с квадратной матрицей коэффициентов:
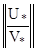 ∙ Y(x
∙ Y(x 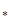 ) =
) = 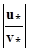 .
.
А в случае «жестких» дифференциальных уравнений предлагается применять построчное ортонормирование матричных краевых условий в процессе их переноса в рассматриваемую точку. Для этого формулы ортонормирования систем линейных алгебраических уравнений можно взять в [Березин, Жидков].
То есть, получив
U  ∙ Y(x
∙ Y(x  ) = u
) = u  ,
,
применяем к этой группе линейных алгебраических уравнений построчное ортонормирование и получаем эквивалентное матричное краевое условие:
U  ∙ Y(x
∙ Y(x  ) = u
) = u  .
.
И теперь уже в это проортонормированное построчно уравнение подставляем
Y(x  ) = K(x
) = K(x  ←x
←x  ) ∙ Y(x
) ∙ Y(x  ) + Y*(x
) + Y*(x  ←x
←x  ) .
) .
И получаем
U  ∙ [ K(x
∙ [ K(x  ←x
←x  ) ∙ Y(x
) ∙ Y(x  ) + Y*(x
) + Y*(x  ←x
←x  ) ] = u
) ] = u 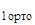 ,
,
[ U 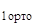 ∙ K(x
∙ K(x 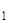 ←x
←x 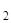 ) ] ∙ Y(x
) ] ∙ Y(x 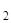 ) = u
) = u 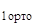 - U
- U 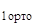 ∙ Y*(x
∙ Y*(x 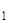 ←x
←x 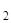 ) ,
) ,
Или получаем краевые условия, перенесенные в точку x 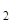 :
:
U 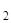 ∙ Y(x
∙ Y(x 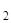 ) = u
) = u 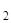 ,
,
где U 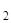 = [ U
= [ U 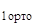 ∙ K(x
∙ K(x 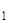 ←x
←x  ) ] и u
) ] и u  = u
= u 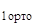 - U
- U 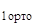 ∙ Y*(x
∙ Y*(x 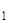 ←x
←x 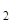 ) .
) .
Теперь уже к этой группе линейных алгебраических уравнений применяем построчное ортонормирование и получаем эквивалентное матричное краевое условие:
U 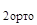 ∙ Y(x
∙ Y(x 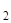 ) = u
) = u  .
.
И так далее.
И аналогично поступаем с промежуточными матричными краевыми условиями, переносимыми с правого края в рассматриваемую точку.
В итоге получаем систему линейных алгебраических уравнений с квадратной матрицей коэффициентов, состоящую из двух независимо друг от друга поэтапно проортонормированных матричных краевых условий, которая решается любым известным методом для получения решения Y(x  ) в рассматриваемой точке x
) в рассматриваемой точке x  :
:
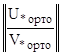 ∙ Y(x
∙ Y(x  ) =
) = 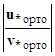 .
.
5 Второй вариант метода «переноса краевых условий» в произвольную точку интервала интегрирования
Этот вариант метода еще не обсчитан на компьютерах.
Предложено выполнять интегрирование по формулам теории матриц [Гантмахер] сразу от некоторой внутренней точки интервала интегрирования к краям:
Y(0) = K(0←x) ∙ Y(x) + Y*(0←x) ,
Y(1) = K(1←x) ∙ Y(x) + Y*(1←x) .
Подставим эти формулы в краевые условия и получим:
U∙Y(0) = u,
U∙[ K(0←x) ∙ Y(x) + Y*(0←x) ] = u,
[ U∙ K(0←x) ] ∙ Y(x) = u - U∙Y*(0←x) .
и
V∙Y(1) = v,
V∙[ K(1←x) ∙ Y(x) + Y*(1←x) ] = v,
[ V∙ K(1←x) ] ∙ Y(x) = v - V∙Y*(1←x) .
То есть получаем два матричных уравнения краевых условий, перенесенные в рассматриваемую точку x:
[ U∙ K(0←x) ] ∙ Y(x) = u - U∙Y*(0←x) ,
[ V∙ K(1←x) ] ∙ Y(x) = v - V∙Y*(1←x) .
Эти уравнения аналогично объединяются в одну систему линейных алгебраических уравнений с квадратной матрицей коэффициентов для нахождения решения Y(x) в любой рассматриваемой точке x:
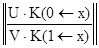 ∙ Y(x) =
∙ Y(x) = 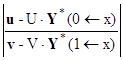 .
.
В случае «жестких» дифференциальных уравнений предлагается следующий алгоритм.
Используем свойство перемножаемости матриц Коши:
K(x 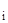 ←x) = K(x
←x) = K(x 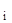 ←x
←x 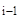 ) ∙ K(x
) ∙ K(x 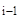 ←x
←x 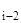 ) ∙ … ∙ K(x
) ∙ … ∙ K(x 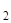 ←x
←x 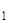 ) ∙ K(x
) ∙ K(x 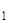 ←x)
←x)
и запишем выражения для матриц Коши, например, в виде:
K(0←x) = K(0←x 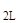 ) ∙ K(x
) ∙ K(x 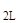 ←x
←x 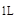 ) ∙ K(x
) ∙ K(x 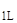 ←x),
←x),
K(1←x) = K(1←x 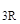 ) ∙ K(x
) ∙ K(x 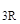 ←x
←x 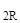 ) ∙ K(x
) ∙ K(x 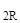 ←x
←x 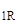 ) ∙ K(x
) ∙ K(x 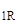 ←x),
←x),
Тогда перенесенные краевые условия можно записать в виде:
[ U∙ K(0←x 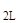 ) ∙ K(x
) ∙ K(x 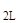 ←x
←x 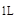 ) ∙ K(x
) ∙ K(x 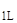 ←x) ] ∙ Y(x) = u - U∙Y*(0←x) ,
←x) ] ∙ Y(x) = u - U∙Y*(0←x) ,
[ V∙ K(1←x 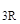 ) ∙ K(x
) ∙ K(x 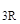 ←x
←x 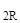 ) ∙ K(x
) ∙ K(x 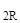 ←x
←x 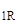 ) ∙ K(x
) ∙ K(x 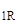 ←x) ] ∙ Y(x) = v - V∙Y*(1←x)
←x) ] ∙ Y(x) = v - V∙Y*(1←x)
или в виде:
[ U∙ K(0←x 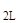 ) ∙ K(x
) ∙ K(x 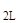 ←x
←x 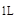 ) ∙ K(x
) ∙ K(x 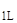 ←x) ] ∙ Y(x) = u* ,
←x) ] ∙ Y(x) = u* ,
[ V∙ K(1←x 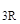 ) ∙ K(x
) ∙ K(x 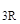 ←x
←x 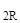 ) ∙ K(x
) ∙ K(x 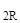 ←x
←x 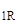 ) ∙ K(x
) ∙ K(x 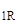 ←x) ] ∙ Y(x) = v* .
←x) ] ∙ Y(x) = v* .
Тогда рассмотрим левое перенесенное краевое условие:
[ U∙ K(0←x 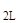 ) ∙ K(x
) ∙ K(x 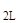 ←x
←x 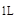 ) ∙ K(x
) ∙ K(x 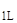 ←x) ] ∙ Y(x) = u* ,
←x) ] ∙ Y(x) = u* ,
[ U∙ K(0←x 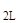 ) ] ∙ { K(x
) ] ∙ { K(x 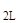 ←x
←x 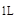 ) ∙ K(x
) ∙ K(x 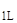 ←x) ∙ Y(x) } = u* ,
←x) ∙ Y(x) } = u* ,
[ матрица ] ∙ { вектор } = вектор .
Эту группу линейных алгебраических уравнений можно подвергнуть построчному ортонормированию, которое сделает строчки [матрицы] ортонормированными, {вектор} затронут не будет, а вектор получит преобразование. То есть получим:
[ U∙ K(0←x 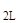 ) ]
) ]  ∙ { K(x
∙ { K(x 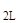 ←x
←x 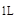 ) ∙ K(x
) ∙ K(x 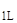 ←x) ∙ Y(x) } = u*
←x) ∙ Y(x) } = u* 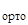 .
.
Далее последовательно можно записать:
[[ U∙ K(0←x 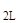 ) ]
) ] 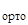 ∙ K(x
∙ K(x 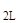 ←x
←x 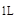 ) ] ∙ { K(x
) ] ∙ { K(x 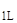 ←x) ∙ Y(x) } = u*
←x) ∙ Y(x) } = u* 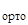 ,
,
[ матрица ] ∙ { вектор } = вектор .
Аналогично и эту группу линейных алгебраических уравнений можно подвергнуть построчному ортонормированию, которое сделает строчки [матрицы] ортонормированными, {вектор} затронут не будет, а вектор получит преобразование. То есть получим:
[[ U∙ K(0←x 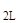 ) ]
) ] 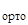 ∙ K(x
∙ K(x 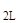 ←x
←x 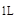 ) ]
) ] 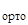 ∙ { K(x
∙ { K(x 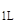 ←x) ∙ Y(x) } = u*
←x) ∙ Y(x) } = u* 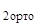 ,
,
Далее аналогично можно записать:
[[[ U∙ K(0←x 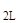 ) ]
) ] 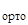 ∙ K(x
∙ K(x 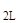 ←x
←x 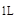 ) ]
) ] 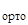 ∙ K(x
∙ K(x 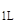 ←x) ] ∙ { Y(x) } = u*
←x) ] ∙ { Y(x) } = u* 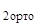 ,
,
[ матрица ] ∙ { вектор} = вектор .
Аналогично и эту группу линейных алгебраических уравнений можно подвергнуть построчному ортонормированию, которое сделает строчки [матрицы] ортонормированными, {вектор} затронут не будет, а вектор получит преобразование. То есть получим:
[[[ U∙ K(0←x 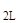 ) ]
) ] 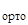 ∙ K(x
∙ K(x 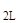 ←x
←x 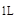 ) ]
) ] 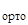 ∙ K(x
∙ K(x 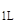 ←x) ]
←x) ] 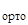 ∙ Y(x) = u*
∙ Y(x) = u* 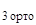 .
.
Аналогично можно проортонормировать матричное уравнение краевых условий и для правого края независимо от левого края.
Далее проортонормированные уравнения краевых условий:
[ U∙ K(0←x) ] 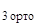 ∙ Y(x) = u*
∙ Y(x) = u* 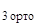 ,
,
[ V∙ K(1←x) ] 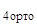 ∙ Y(x) = v*
∙ Y(x) = v* 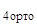
как и ранее объединяются в одну обычную систему линейных алгебраических уравнений с квадратной матрицей коэффициентов для нахождения искомого вектора Y(x) :
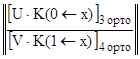 ∙ Y(x) =
∙ Y(x) = 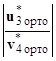 .
.
Дата: 2019-07-25, просмотров: 163.