Можно построить дешифратор со сложностью 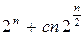 , где
, где 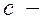 некоторая константа, не зависящая от
некоторая константа, не зависящая от 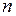 .
.
Очевидно, что сложность дешифратора, имеющего 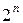 выходов, не может быть меньше чем
выходов, не может быть меньше чем 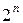 , т. е.
, т. е. 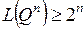 .
.
Получим оценку сверху.
Пусть 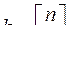 – целая часть от
– целая часть от 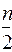 . Возьмем 2 дешифратора
. Возьмем 2 дешифратора 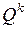 и
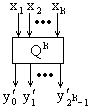
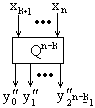
и 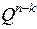 , направим
, направим 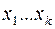 на входы
на входы 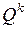 ,
, 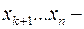 на входы
на входы 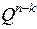 (рис. 6.12).
(рис. 6.12).
| 
|
| Рис. 6.12 | |
Обозначим выходы первого 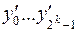 , второго дешифратора
, второго дешифратора 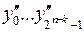 . Затем возьмем конъюнкцию
. Затем возьмем конъюнкцию 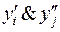 , где
, где 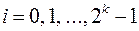 ,
, 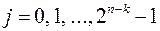 , т. е. конъюнкцию каждого выхода первого дешифратора с каждым выходом второго (рис. 6.13).
, т. е. конъюнкцию каждого выхода первого дешифратора с каждым выходом второго (рис. 6.13).
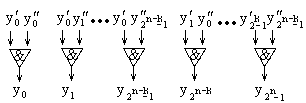 Рис. 6.13
Рис. 6.13
|
Получим 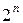 выходов
выходов 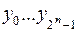 . Если на вход дешифратора поступил набор
. Если на вход дешифратора поступил набор 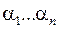 , т. е.
, т. е. 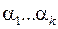 на вход дешифратора
на вход дешифратора 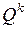 и
и 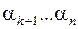 на вход
на вход 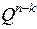 , то на выходе дешифратора
, то на выходе дешифратора  , на выходе
, на выходе 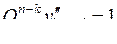 , именно конъюнкция этих выходов должна получить номер
, именно конъюнкция этих выходов должна получить номер 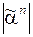 и
и 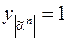 .
.
Оценим сложность 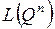 , но прежде напомним очевидные неравенства:
, но прежде напомним очевидные неравенства:
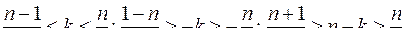 .
.
Тогда
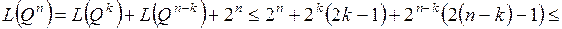
 .
.
Такой дешифратор позволяет получить упрощенную схему для реализации любой функции алгебры логики.
Теорема. Любую функцию алгебры логики 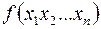 можно реализовать в стандартном базисе схемой со сложностью
можно реализовать в стандартном базисе схемой со сложностью 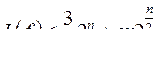 .
.
Если 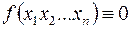 , она реализуется тривиальной схемой. Если
, она реализуется тривиальной схемой. Если 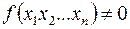 , то ее можно задать совершенной дизъюнктивной нормальной формой
, то ее можно задать совершенной дизъюнктивной нормальной формой
 .
.
Пусть 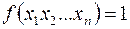 на
на 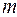 наборах.
наборах.
1. Пусть 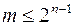 , т. е. меньше половины наборов. Возьмем улучшенный дешифратор
, т. е. меньше половины наборов. Возьмем улучшенный дешифратор 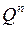 , выберем выходы, номера которых есть десятичные коды наборов, на которых
, выберем выходы, номера которых есть десятичные коды наборов, на которых 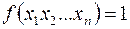 .
.
Например, 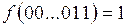 , десятичный код этого набора 3, тогда , десятичный код этого набора 3, тогда 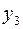 будет среди выбранных выходов. Затем возьмем дизъюнкцию этих выходов (рис. 6.14). будет среди выбранных выходов. Затем возьмем дизъюнкцию этих выходов (рис. 6.14).
| 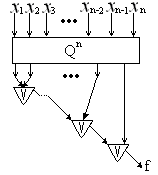 Рис. 6.14
Рис. 6.14
|
Если поступил набор 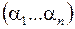 и
и 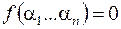 , тогда
, тогда 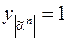 , но этот выход не вошел в дизъюнкцию, а на остальных выходах имеем
, но этот выход не вошел в дизъюнкцию, а на остальных выходах имеем 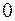 и
и 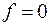 . Если поступил набор
. Если поступил набор 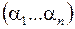 и
и 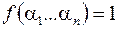 , то
, то 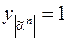 и этот выход вошел в нашу дизъюнкцию,
и этот выход вошел в нашу дизъюнкцию, 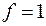 .
.
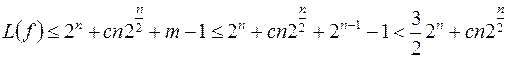 .
.
2. Пусть 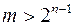 , тогда рассмотрим функцию , тогда рассмотрим функцию 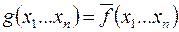 . . 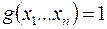 на на 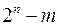 наборах, а наборах, а 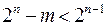 . Реализуем функцию . Реализуем функцию 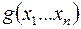 , а затем возьмем ее отрицание (рис. 6.15). , а затем возьмем ее отрицание (рис. 6.15).
| 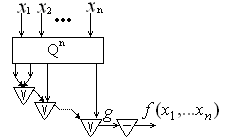 Рис. 6.15
Рис. 6.15
|
 .
.
Шифратор n -го порядка ( 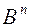 ).
).
Шифратор преобразует десятичный код в двоичный. Он имеет 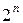 входов:
входов: 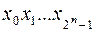 и
и 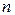 выходов
выходов 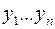 . Десятичное число подается по адресу, т. е. если в шифратор подается число
. Десятичное число подается по адресу, т. е. если в шифратор подается число 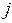 , то
, то 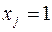 , а на все остальные входы подается
, а на все остальные входы подается 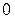 . На выходе
. На выходе 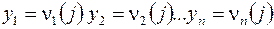 .
.
Теорема о шифраторе n -го порядка .
Можно построить схему, осуществляющую такую процедуру, со сложностью 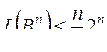 .
.
Для этого на каждом выходе 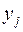 надо реализовать функцию
надо реализовать функцию 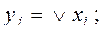
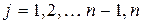 . Тогда
. Тогда 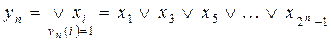

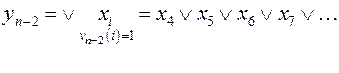
Будет нагляднее, если мы рассмотрим 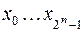 и
и 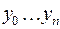 в виде таблицы (табл. 6.1).
в виде таблицы (табл. 6.1).
Таблица 6.1
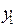
| 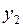
| 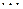
| 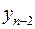
| 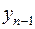
| 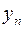
| |
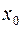
| 0 | 0 | 
| 0 | 0 | 0 |
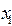
| 0 | 0 | 
| 0 | 0 | 1 |
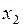
| 0 | 0 | 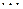
| 0 | 1 | 0 |
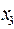
| 0 | 0 | 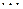
| 0 | 1 | 1 |
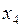
| 0 | 0 | 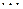
| 1 | 0 | 0 |
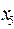
| 0 | 0 | 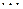
| 1 | 0 | 1 |
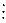
| 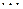
| |||||
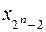
| 1 | 1 | 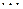
| 1 | 1 | 0 |
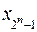
| 1 | 1 | 
| 1 | 1 | 1 |
Если, например, 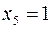 , то все остальные
, то все остальные 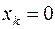 и эта 1 вошла в качестве дизъюнктивного слагаемого именно в те разряды, где в двоичном коде числа 5 стоит 1.
и эта 1 вошла в качестве дизъюнктивного слагаемого именно в те разряды, где в двоичном коде числа 5 стоит 1.
Оценим сложность. У нас 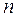 выходов и на каждом выходе берется дизъюнкция
выходов и на каждом выходе берется дизъюнкция 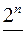 слагаемых (в каждом столбце табл. 6.1 равное число 0 и 1). Поэтому
слагаемых (в каждом столбце табл. 6.1 равное число 0 и 1). Поэтому 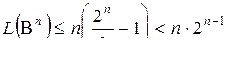 .
.
Мультиплексор n -го порядка 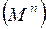 .
.
Мультиплексор – схема, имеющая 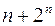 входов:
входов: 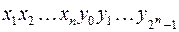 и один выход:
и один выход: 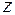 . Причем если на вход посылается набор
. Причем если на вход посылается набор 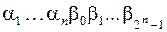 , то
, то 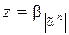 . Мультиплексор – переключатель, который может менять как номер канала, из которого берется информация, так и саму информацию.
. Мультиплексор – переключатель, который может менять как номер канала, из которого берется информация, так и саму информацию.
Теорема о мультиплексоре n-го порядка.
Можно построить схему, осуществляющую указанную процедуру со сложностью  .
.
Входы 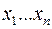 направляем в дешифратор с уменьшенной сложностью, возьмем конъюнкцию выхода дешифратора
направляем в дешифратор с уменьшенной сложностью, возьмем конъюнкцию выхода дешифратора 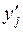 со входом
со входом 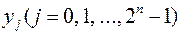 , а затем возьмем дизъюнкцию всех полученных конъюнкций (рис. 6.16).
, а затем возьмем дизъюнкцию всех полученных конъюнкций (рис. 6.16).
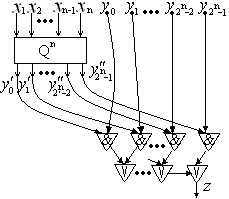 Рис. 6.16
Рис. 6.16
|
Пусть на вход подан набор 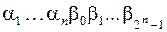 , тогда
, тогда 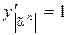 , остальные
, остальные 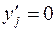 .
. 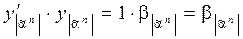 , остальные конъюнкции равны 0,
, остальные конъюнкции равны 0, 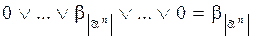 , таким образом,
, таким образом, 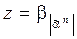 . Cложность мультиплексора
. Cложность мультиплексора 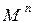 складывается из сложности дешифратора,
складывается из сложности дешифратора, 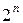 конъюнкций и
конъюнкций и 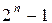 дизъюнкций
дизъюнкций
 .
.
Пример. Построить дешифратор 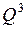 уменьшенной сложности и с его помощью реализовать функцию
уменьшенной сложности и с его помощью реализовать функцию 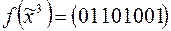 .
.
В этом случае 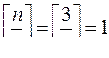 , один дешифратор будет
, один дешифратор будет 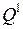 , другой
, другой 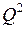 (рис. 6.17).
(рис. 6.17).
Если посылается набор 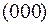 , дешифратор выдает 1 на выходе
, дешифратор выдает 1 на выходе 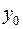 , на остальных выходах будут 0 и
, на остальных выходах будут 0 и 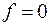 . Если послать набор
. Если послать набор 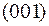 на выходе
на выходе 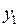 будет 1 и
будет 1 и 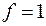 . Если поступает набор (010), на выходе
. Если поступает набор (010), на выходе 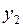 будет 1 и
будет 1 и 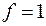 . Если поступает набор (011) на выходе
. Если поступает набор (011) на выходе 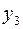 будет 1, на остальных выходах будет 0 и
будет 1, на остальных выходах будет 0 и 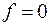 . На наборе (100) функция будет равна 1, на наборах (101) и (110) получим 0 и на наборе (111) получим 1.
. На наборе (100) функция будет равна 1, на наборах (101) и (110) получим 0 и на наборе (111) получим 1.
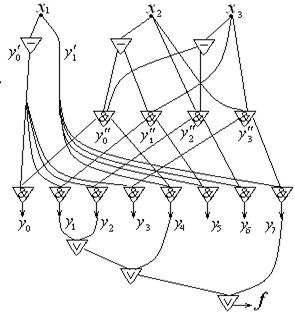 Рис. 6.17
Рис. 6.17
|
Задачи и упражнения по СФЭ
1. Для заданной функции 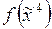 построить СФЭ в стандартном базисе сложности, не превосходящей m.
построить СФЭ в стандартном базисе сложности, не превосходящей m.
1) 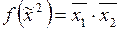 ,
, 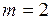 ;
;
2) 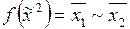 ,
, 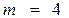 ;
;
3) 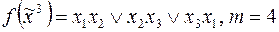 ;
;
4) 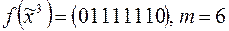 ;
;
5) 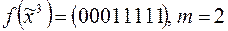 ;
;
6) 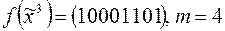 ;
;
7) 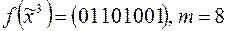 .
.
8)
2. Реализовать функцию 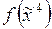 СФЭ в стандартном базисе, предварительно упростив выражение для
СФЭ в стандартном базисе, предварительно упростив выражение для 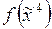 .
.
1) 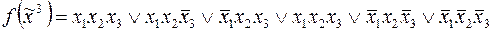 ;
;
2) 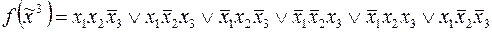 ;
;
3) 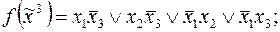
4) 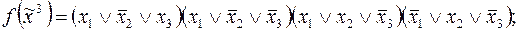
5) 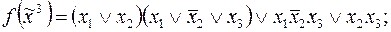
6) 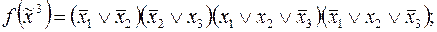
7) 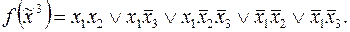
3. Реализовать функцию 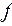 по методу, основанному на ДНФ.
по методу, основанному на ДНФ.
1) 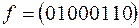 ; 4)
; 4) 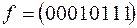 ;
;
2) 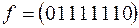 ; 5)
; 5) 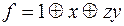 ;
;
3) 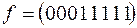 ; 6)
; 6) 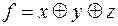 .
.
Глубинной CФЭ в базисе 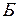 называется максимальное число функциональных элементов в ориентированных цепях, соединяющих вход с выходом.
называется максимальное число функциональных элементов в ориентированных цепях, соединяющих вход с выходом.
4. Построить CФЭ глубины 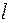 .
.
1) 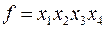 ,
, 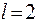 ;
;
2) 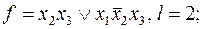
3) 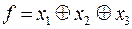 ,
, 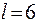 ;
;
4) 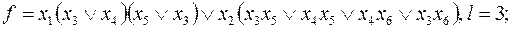
5) 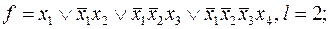
6) 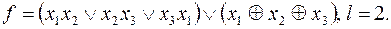
Дата: 2019-04-23, просмотров: 264.