Если в связном планарном графе  , где
, где  ,
,  , нет циклов длины меньше
, нет циклов длины меньше  , то
, то
 .
.
Доказательство. Рассмотрим геометрическую реализацию графа на плоскости. Пусть r – число граней и  – число сторон, окружающих i-ю грань, тогда
– число сторон, окружающих i-ю грань, тогда  и
и  , так как каждое ребро разделяет две грани и поэтому учитывается дважды.
, так как каждое ребро разделяет две грани и поэтому учитывается дважды.
 и
и  ,
,
отсюда  и
и  , откуда вытекает требуемое неравенство.
, откуда вытекает требуемое неравенство.
Замечание. Если  – простой связный планарный граф, то в нем нет циклов длины меньше трех, поэтому
– простой связный планарный граф, то в нем нет циклов длины меньше трех, поэтому  .
.
Теорема о непланарности графов  и
и 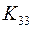 . В графе
. В графе 
 . Если он планарен, то
. Если он планарен, то  , т. е.
, т. е.  – противоречие.
– противоречие.
В графе 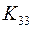
 . Если он планарен, то
. Если он планарен, то  –противоречие.
–противоречие.
Определение. Операцией подразбиения ребра  называется удаление этого ребра из графа, добавление новой вершины
называется удаление этого ребра из графа, добавление новой вершины 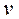 к
к  и двух новых ребер
и двух новых ребер  и
и  к множеству
к множеству 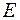 (рис. 5.16).
(рис. 5.16).
 Рис. 5 .16
Рис. 5 .16
|
Определение. Граф 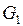 называется подразбиением графа
называется подразбиением графа  , если он может быть получен из G путем конечного числа подразбиений ребер.
, если он может быть получен из G путем конечного числа подразбиений ребер.
Из определения следует, что граф 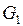 будет отличаться от графа G только вершинами степени 2.
будет отличаться от графа G только вершинами степени 2.
Определение. Два графа G и H называются гомеоморфными, если существуют их подразбиения, которые изоморфны друг другу.
Пример. На рис. 5.17 изображены гомеоморфные графы.

Рис. 5.17
Теорема Понтрягина-Куратовского (без доказательства). Граф  планарен тогда и только тогда, когда не содержит подграфов, гомеоморфных
планарен тогда и только тогда, когда не содержит подграфов, гомеоморфных  или
или 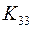 .
.
Эта теорема была доказана в 1930 г. советским математиком Львом Cеменовичем Понтрягиным и независимо от него польским математиком Казимиром Куратовским, и является критерием планарности графа.
Задача. Показать, что граф, изображенный на рис. 5.18, непланарен.

Рис. 5.18 Рис. 5.19 Рис. 5.20
Выделим подграф (рис. 5.19), он гомеоморфен графу 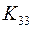 (рис. 5.20).
(рис. 5.20).
Раскраска вершин графа
Определение. Пусть  – произвольное множество элементов, называемых цветами или красками, тогда отображение
– произвольное множество элементов, называемых цветами или красками, тогда отображение  , где
, где  – множество вершин графа
– множество вершин графа  , называется раскраской вершин графа.
, называется раскраской вершин графа.
Раскраска называется правильной, если для любого ребра  .
.
Определение. Граф  – раскрашиваем, если его можно правильно раскрасить
– раскрашиваем, если его можно правильно раскрасить  цветами.
цветами.
Если граф  – раскрашиваем, но его нельзя правильно раскрасить
– раскрашиваем, но его нельзя правильно раскрасить 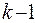 цветом, граф называется k -хроматическим, в этом случае
цветом, граф называется k -хроматическим, в этом случае  – хроматическое число графа
– хроматическое число графа  .
.
Граф 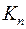 , например, n -хроматический, любой двудольный граф 2-хроматический.
, например, n -хроматический, любой двудольный граф 2-хроматический.
Теорема о раскраске произвольного графа. Если в графе  , то граф
, то граф 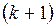 – раскрашиваем.
– раскрашиваем.
Доказательство методом индукции по числу вершин.
Если  , то
, то  и ее можно выкрасить одним цветом.
и ее можно выкрасить одним цветом.
Пусть  и граф
и граф 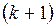 – раскрашиваем.
– раскрашиваем.
Рассмотрим граф с p вершинами,  . Удалим одну вершину со всеми инцидентными ребрами. Получим граф
. Удалим одну вершину со всеми инцидентными ребрами. Получим граф  и
и  . Тогда по индуктивному предположению граф
. Тогда по индуктивному предположению граф  – раскрашиваем. Добавим удаленную вершину со всеми инцидентными ребрами. Она будет иметь максимум
– раскрашиваем. Добавим удаленную вершину со всеми инцидентными ребрами. Она будет иметь максимум  смежных вершин, выкрасим ее в
смежных вершин, выкрасим ее в 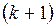 -й цвет, получим правильную раскраску графа G.
-й цвет, получим правильную раскраску графа G.
Для раскраски планарного графа достаточно 5 цветов, правда, более 100 лет существует гипотеза «четырех красок», до сих пор не опровергнутая и не доказанная. Компьютерное моделирование планарных графов с числом вершин меньше 52 показало справедливость этой гипотезы для графов с  .
.
Мы докажем теорему о достаточности 5 цветов для планарных графов, но прежде докажем лемму.
Лемма о существовании вершины степени 5. Пусть G – простой (т. е. без кратных ребер и петель), планарный граф, тогда в нем существует вершина, степень которой не превосходит 5.
Доказательство. Пусть 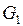 – связная компонента планарного графа,
– связная компонента планарного графа, 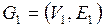 , пусть
, пусть  .
.  . Пусть
. Пусть  для любой вершины
для любой вершины  , тогда
, тогда  . C другой стороны, в планарном графе без кратных ребер и петель
. C другой стороны, в планарном графе без кратных ребер и петель  , мы пришли к противоречию
, мы пришли к противоречию
 ,
,
что и доказывает лемму.
Теорема о достаточности пяти цветов. Любой планарный граф без петель 5 – раскрашиваем.
Доказательство. При наличии петель граф не может быть правильно раскрашенным, так как концы любого ребра должны быть выкрашены в разные цвета.
При доказательстве теоремы мы воспользуемся леммой, в которой существенным требованием было отсутствие кратных ребер. Для правильной раскраски графа кратные ребра не играют никакой роли. На рис. 5.21 показано, что кратные ребра мы можем воспринимать как одно ребро.
 Рис. 5 .21
Рис. 5 .21
|
Если граф несвязный, то задача сводится к правильной раскраске каждой связной компоненты.
Поэтому пусть  – простой планарный связный граф. Теорему будем доказывать по индукции, по числу вершин.
– простой планарный связный граф. Теорему будем доказывать по индукции, по числу вершин.
Пусть  , тогда раскрасим эту вершину одним цветом.
, тогда раскрасим эту вершину одним цветом.
Пусть для графов с  утверждение верно.
утверждение верно.
Пусть  , рассмотрим геометрическую реализацию графа на плоскости. По лемме у графа существует вершина
, рассмотрим геометрическую реализацию графа на плоскости. По лемме у графа существует вершина 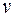 такая, что
такая, что  . Удалим эту вершину вместе с инцидентными ребрами, получим граф
. Удалим эту вершину вместе с инцидентными ребрами, получим граф  , он планарен, число вершин у него
, он планарен, число вершин у него  , по индуктивному предположению он 5-раскрашиваем.
, по индуктивному предположению он 5-раскрашиваем.
Вернем вершину 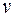 со всеми инцидентными ребрами. Пусть вершина
со всеми инцидентными ребрами. Пусть вершина 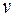 смежна с вершинами
смежна с вершинами  , где
, где  .
.
Возможны три варианта:
1.  , т. е. она смежна с четырьмя или менее вершинами. Если даже все эти вершины выкрашены в разные цвета, то есть пятый цвет, в который можно выкрасить эту вершину.
, т. е. она смежна с четырьмя или менее вершинами. Если даже все эти вершины выкрашены в разные цвета, то есть пятый цвет, в который можно выкрасить эту вершину.
2.  , но среди цветов вершин, с которыми смежна вершина, есть повторяющиеся цвета, тогда вновь остается запасной цвет для вершины v.
, но среди цветов вершин, с которыми смежна вершина, есть повторяющиеся цвета, тогда вновь остается запасной цвет для вершины v.
3.  и все вершины, смежные с ней, выкрашены в разные цвета.
и все вершины, смежные с ней, выкрашены в разные цвета.
Занумеруем вершины, смежные с 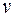 и обозначим цвет вершины
и обозначим цвет вершины  через
через  , как показано на рис. 5.20.
, как показано на рис. 5.20.
 Рис. 5 .22
Рис. 5 .22
| Пусть  – связное множество вершин, до которых можно дойти из вершины – связное множество вершин, до которых можно дойти из вершины 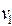 , идя по вершинам цветов , идя по вершинам цветов  и и  . Вершина . Вершина 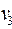 либо войдет в либо войдет в  , либо нет. Рис. 5.22 иллюстрирует именно этот случай. Тогда в множестве , либо нет. Рис. 5.22 иллюстрирует именно этот случай. Тогда в множестве  поменяем цвета поменяем цвета  на на  и и  на на  . .
|
При этом раскраска графа останется правильной, так как в 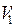 вошли все смежные вершины цветов
вошли все смежные вершины цветов  и
и  , но вершина
, но вершина 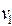 будет выкрашена в цвет
будет выкрашена в цвет  , тогда вершину
, тогда вершину 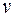 выкрасим в цвет
выкрасим в цвет  .
.
 Рис. 5 .23
Рис. 5 .23
| Если вершина  , как показано на рис. 5.23, то перекрашивать вершины в множестве , как показано на рис. 5.23, то перекрашивать вершины в множестве  в этом случае бесполезно. в этом случае бесполезно.
|
Тогда рассмотрим множество 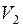 – связное множество вершин, до которых можно дойти из вершины
– связное множество вершин, до которых можно дойти из вершины  , идя по вершинам цветов
, идя по вершинам цветов  и
и  . Вершина
. Вершина  (рис. 5.23), так как она отделена от вершины
(рис. 5.23), так как она отделена от вершины  циклом. Путь из
циклом. Путь из  в
в  не может пересечь ребро – мы рассмотрели геометрическую реализацию графа на плоскости. Этот путь не может пройти и через вершину цикла, поскольку все вершины цикла окрашены в цвета
не может пересечь ребро – мы рассмотрели геометрическую реализацию графа на плоскости. Этот путь не может пройти и через вершину цикла, поскольку все вершины цикла окрашены в цвета  и
и  .
.
Поменяем в множестве 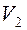 цвета
цвета  на
на  ,
,  на
на  и выкрасим вершину
и выкрасим вершину 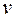 в цвет
в цвет  .
.
C задачей о раскраске графа связана, например, задача о раскраске географической карты, где соседние страны должны быть выкрашены в разные цвета. Cтранам сопоставим вершины графа, соседним странам соответствуют смежные вершины, которые должны быть выкрашены в разные цвета. Полученный граф будет плоским, следовательно, для его правильной раскраски достаточно пяти цветов.
Дата: 2019-04-23, просмотров: 207.