Ограниченно-детерминированная функция является математической моделью функционирования реального дискретного преобразователя (автомата), который имеет несколько внутренних состояний («память») и при поступлении одного и того же сигнала (входного набора переменных  ) вырабатывает выходной сигнал в зависимости от того, в каком состоянии он находился в этот момент времени. Классы эквивалентности моделируют внутренние состояния автомата.
) вырабатывает выходной сигнал в зависимости от того, в каком состоянии он находился в этот момент времени. Классы эквивалентности моделируют внутренние состояния автомата.
Обратимся к диаграмме Мура для автоматной функции  . Пусть в момент времени
. Пусть в момент времени  автомат находился в состоянии
автомат находился в состоянии  ,
,
тогда при поступлении в момент t сигнала  по дуге с номером
по дуге с номером  , соответствующим этому сигналу, автомат переходит в состояние
, соответствующим этому сигналу, автомат переходит в состояние  и вырабатывается выходной сигнал
и вырабатывается выходной сигнал  , который приписан этой дуге (рис. 7.5).
, который приписан этой дуге (рис. 7.5).

|
Рис. 7.5
Таким образом, величины  и
и  однозначно определяются по
однозначно определяются по  и
и  .
.
Пусть в момент t переменная  описывает значения входного сигнала,
описывает значения входного сигнала,  описывает значения состояния,
описывает значения состояния,  – значения выходного сигнала, тогда
– значения выходного сигнала, тогда


Эти уравнения называются каноническими уравнениями автоматной функции в векторной форме. Функция F называется функцией выходов, G – функцией переходов. Если задано начальное состояние автомата  , автомат называется инициальным.
, автомат называется инициальным.  – класс эквивалентности, к которому относится корень занумерованного дерева, часто
– класс эквивалентности, к которому относится корень занумерованного дерева, часто  =0, но это не обязательное требование.
=0, но это не обязательное требование.
Получим канонические уравнения автоматной функции в скалярной форме. Множество Q состоит из чисел  , где
, где 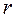 – вес автоматной функции, закодируем эти числа двоичными кодами. Пусть
– вес автоматной функции, закодируем эти числа двоичными кодами. Пусть 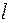 – минимальное целое число, такое, что
– минимальное целое число, такое, что  или
или  – целая часть сверху числа
– целая часть сверху числа  , тогда все числа от
, тогда все числа от  до r – 1 можно закодировать
до r – 1 можно закодировать 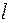 - разрядными двоичными кодами
- разрядными двоичными кодами  .
.
В предыдущем параграфе мы рассматривали автоматную функцию, вырабатывающую одну выходную последовательность  Не меняя рассуждений и лишь усложнив запись, можно считать, что автомат имеет m выходов и вырабатывает выходную последовательность
Не меняя рассуждений и лишь усложнив запись, можно считать, что автомат имеет m выходов и вырабатывает выходную последовательность  Запишем канонические уравнения в скалярной форме для этого более общего случая:
Запишем канонические уравнения в скалярной форме для этого более общего случая:

 .
.
Пример 4. Получим канонические уравнения автоматной функции, рассмотренной в примере 1.
Построим сначала каноническую таблицу. Вес этой функции равен 2, поэтому  . В левой части канонической таблицы стоят переменные
. В левой части канонической таблицы стоят переменные  и
и  , в правой части – функции
, в правой части – функции  и
и  , значения которых берем с усеченного дерева (рис. 7.3) или с диаграммы Мура (рис. 7.4). Если
, значения которых берем с усеченного дерева (рис. 7.3) или с диаграммы Мура (рис. 7.4). Если 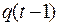 было равно 0 (корень дерева) и входной сигнал был
было равно 0 (корень дерева) и входной сигнал был  , то
, то  , и переходим в состояние
, и переходим в состояние  . Если
. Если 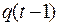 было равно 1, то по дуге, соответствующей входному сигналу
было равно 1, то по дуге, соответствующей входному сигналу  , переходим снова в состояние 0, но
, переходим снова в состояние 0, но  . Cняв информацию со всех дуг усеченного дерева, получим табл. 7.1.
. Cняв информацию со всех дуг усеченного дерева, получим табл. 7.1.
Таблица 7.1
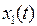
| 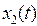
| 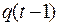
| 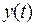
| 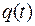
|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
В каждый момент времени t эта каноническая таблица является таблицей истинности для булевых функций 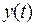 и
и 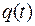 , которые можно задать формулами, например, в виде СДНФ или ДНФ или любыми другими
, которые можно задать формулами, например, в виде СДНФ или ДНФ или любыми другими

Пример 5. Построить канонические уравнения для автоматной функции, имеющей один вход и один выход:

Построим сначала информативное дерево (рис. 7.6).

|
Рис. 7.6
Найдем вес функции  , построим усеченное дерево (рис. 7.7).
, построим усеченное дерево (рис. 7.7).

|
Рис. 7.7
Диаграмма Мура для этой функции изображена на рис. 7.8 сплошной линией.

|
Рис. 7.8
Закодируем состояния  ,
,  ,
,  и построим каноническую табл. 7.2.
и построим каноническую табл. 7.2.
Таблица 7.2
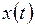
| 
| 
| 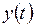
| 
| 
|
| 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 | 1 |
Функции 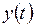 ,
,  ,
,  заданы на 6 наборах из 8, так как набор
заданы на 6 наборах из 8, так как набор  принимает только 3 значения. Доопределим наши функции на наборах (011) и (111) таким образом, чтобы получить наиболее простые формулы для их задания. Такое доопределение означает, что мы ввели дополнительное состояние и две дуги, которые на диаграмме Мура (рис. 7.8) изображены пунктиром. Введенное состояние будет недостижимым, так как нет ни одной дуги, входящей в эту вершину графа, и не скажется на функционировании автомата, хотя вид полученных уравнений может быть различным. Запишем канонические уравнения:
принимает только 3 значения. Доопределим наши функции на наборах (011) и (111) таким образом, чтобы получить наиболее простые формулы для их задания. Такое доопределение означает, что мы ввели дополнительное состояние и две дуги, которые на диаграмме Мура (рис. 7.8) изображены пунктиром. Введенное состояние будет недостижимым, так как нет ни одной дуги, входящей в эту вершину графа, и не скажется на функционировании автомата, хотя вид полученных уравнений может быть различным. Запишем канонические уравнения:



 .
.
В общем случае функции  ,
,  задаются на
задаются на  наборах длины
наборах длины  . Доопределив их на недостающих, мы получим булевы функции и система канонических уравнений примет вид:
. Доопределив их на недостающих, мы получим булевы функции и система канонических уравнений примет вид:

Пример 6. Построить диаграмму Мура, каноническую таблицу и канонические уравнения для функции  . (Здесь
. (Здесь  означает бесконечную последовательность 1).
означает бесконечную последовательность 1).
Построим информативное дерево.
 Рис. 7.9
Рис. 7.9
|  Рис. 7.10
Рис. 7.10
|
Cостояние в корне обозначим 0 (хотя это не обязательно), вершины первого яруса порождают одинаковые поддеревья, отличные от основного дерева, обозначим их 1. Вершины третьего яруса порождают одинаковые поддеревья, отнесем их ко второму классу эквивалентности. Итак, вес дерева равен 3. Cоответствующее усеченное дерево приведено на рис. 7.10, диаграмма Мура – на рис. 7.11.

|
Рис. 7.11
Каноническая табл. 7.3. для этой функции имеет вид:
Таблица 7.3

| 
| 
| 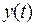
| 
| 
|
| 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 | 1 |
Выделенные пунктиром строчки, соответствующие недостижимому состоянию 3, заполним произвольным образом.
Для функций  и
и  переменная x – фиктивная.
переменная x – фиктивная.

 ;
;
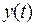 запишем в виде ДНФ:
запишем в виде ДНФ:

 .
.
Пример 7. Построить канонические уравнения функции  , если
, если 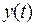 есть t-я цифра после запятой в двоичном разложении числа 5/7.
есть t-я цифра после запятой в двоичном разложении числа 5/7.
Двоичный код числа 5/7 будет  ,
, 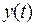 не зависит от
не зависит от  , зависит только от момента времени:
, зависит только от момента времени:  , и эта последовательность периодически повторяется. Поэтому можно сразу строить усеченное дерево (рис. 7.12) и диаграмму Мура (рис. 7.13).
, и эта последовательность периодически повторяется. Поэтому можно сразу строить усеченное дерево (рис. 7.12) и диаграмму Мура (рис. 7.13).
 Рис. 7.12 Рис. 7.12
|
 Рис. 7.13
Рис. 7.13
|
Каноническая табл. 7.4. для этой функции имеет вид:
Таблица 7.4

| 
| 
| 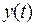
| 
| 
|
| 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 |
Мы получаем простые канонические уравнения

Пример 8. Найти вес автоматной функции, заданной диаграммой Мура на рис. 7.14.
Cостояние 4 – недостижимое состояние, поэтому эту вершину вместе с выходящими дугами можно убрать.
 Рис. 7.14
Рис. 7.14
|
Построим дерево; состояние 1~2, 5~0~3 и вес равен 2.
 Рис. 7.15
Рис. 7.15
|
Построим усеченное дерево веса 2 и приведенную (без лишних вершин) диаграмму Мура.

| 
|
Рис. 7.16
Дата: 2019-04-23, просмотров: 282.