Сущность вариационной пульсометрии заключается в изучении закона распределения кардиоинтервалов как случайных величин. При этом строится вариационная кривая (кривая распределения кардиоинтервалов – гистограмма) и определяются ее основные характеристики: Мо (Мода), Амо (амплитуда моды), MxDMn (вариационный размах). Мода – это наиболее часто встречающееся в данном динамическом ряде значение кардиоинтервала. При нормальном распределении и высокой стационарности исследуемого процесса Мо мало отличается от математического ожидания (М). Амо – (амплитуда моды) – это число кардиоинтервалов, соответствующих значению моды, в % к объему выборки. Вариационный размах (MxDMn) отражает степень вариативности значений кардиоинтервалов в исследуемом динамическом ряду. Он вычисляется по разности максимального (Mx) и минимального (Mn) значений кардиоинтервалов и поэтому при аритмиях или артефактах может быть искажен.

При построении гистограмм (или вариационных пульсограмм) первостепенное значение имеет выбор способа группировки данных. В многолетней практике сложился традиционный подход к группировке кардиоинтервалов в диапазоне от 400 до 1300 мс. с интервалом в 50 мс. Таким образом, выделяются 20 фиксированных диапазонов длительностей кардиоинтервалов, что позволяет сравнивать вариационные пульсограммы, полученные разными исследователями на разных группах исследований. При этом объем выборки, в которой производится группировка и построение вариационной пульсограммы, также стандартный – 5 минут. Другой способ построения вариационных пульсограмм заключается в том, чтобы вначале определить модальное значение кардиоинтервала, а затем, используя диапазоны по 50 мс, формировать гистограмму в обе стороны от моды. Вариационная пульсограмма может быть также представлена «гладким» графиком плотности распределения ( см. рис. 3).

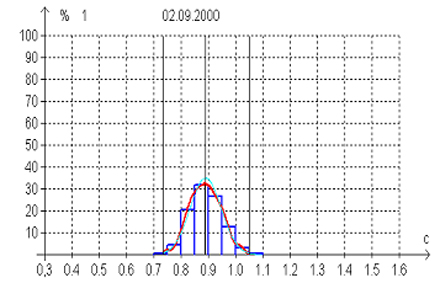
Рис. 3. Образцы вариационных пульсограмм при тахикардии и нормокардии.

По данным вариационной пульсометрии вычисляется широко распространенный в России индекс напряжения регуляторных систем или стресс-индекс.

Ин = АМо/2Mо* MxDMn.

Западноевропейские и американские исследователи используют апроксимацию кривой распределения кардиоинтервалов треугольником и вычисляют так называемый триангулярный индекс - интеграл плотности распределения (общее количество кардиоинтервалов) отнесенный к максимуму плотности распределения (АМо). Этот показатель обозначается как TINN (triangular interpolation of NN intervals).

Кроме того, используется построение гистограмм по разностным значениям соседних кардиоинтервалов с аппроксимацией их экспоненциальной кривой и вычислением логарифмического коэффициента, а также другие способы аппроксимации.

Автокорреляционный анализ

Вычисление и построение автокорреляционной функции динамического ряда кардиоинтервалов направлено на изучение внутренней структуры этого ряда как случайного процесса. Автокорреляционная функция представляет собой график динамики коэффициентов корреляции, получаемых при последовательном смещении анализируемого динамического ряда на одно число по отношению к своему собственному ряду.

После первого сдвига на одно значение коэффициент корреляции тем меньше единицы, чем более выражены дыхательные волны (см. рис. 4 вверху). Если в исследуемой выборке доминируют медленноволновые компоненты, то коэффициент корреляции после первого сдвига будет лишь незначительно ниже единицы (см. рис. 4 в середине и внизу). Последующие сдвиги ведут к постепенному уменьшению корреляционных коэффициентов. Автокоррелограмма позволяет судить о скрытой периодичности СР.

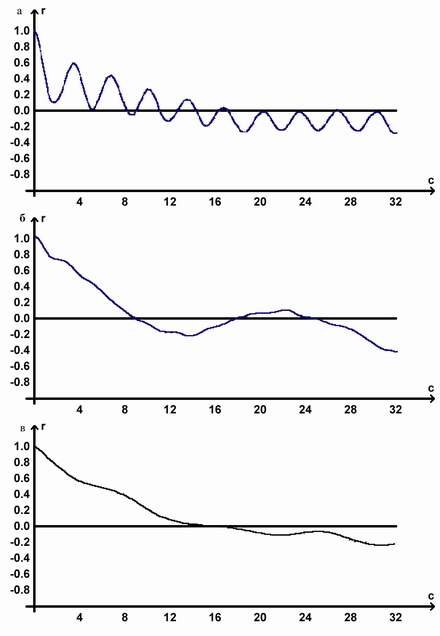
Рис. 4. Образцы автокоррелограмм с выраженными дыхательными волнами (вверху), с преобладанием медленных (в середине) и очень медленных ( внизу) волн.

В качестве количественных показателей автокоррелограммы рекомендуются С1 – значение коэффициента корреляции после первого сдвига и С0 – число сдвигов в результате которого значение коэффициента корреляции становиться отрицательным