Для нахождения альтернативного решения для клетки с нулевой оценкой строят еще один цикл перераспределения поставок по тем же правилам, что и при улучшении решения. Проверка оптимальности решения для альтернативного решения не производится. Следует проверить значение целевой функции, соответствующее альтернативному решению: оно должно совпадать со значением целевой функции, соответствующим первому оптимальному решению.
Найдем одно из альтернативных решений. Для этого для клетки с нулевой оценкой строим еще один цикл: 0*-9-6-15-0* (все вершины цикла, кроме первой, находятся в занятых клетках, углы прямые, число вершин четное). У вершин цикла с соответствующими значениями поставок по правилу чередования знаков ставим знаки (+) и (–), начиная со свободной клетки. У вершин со знаком (–) выбираем минимальный груз q = min[9, 15] = 9.
Его прибавляем к грузам, стоящим у положительных вершин, и отнимаем от грузов, стоящих у отрицательных вершин. Получаем новый цикл:
Получили альтернативное решение задачи (план перевозок):
Значение целевой функции:
.
Значение целевой функции альтернативного решения совпало со значением целевой функции первого оптимального решения транспортной задачи.
Таким образом, решение транспортной задачи:
, 
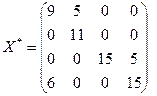, L(X*) = 381.
Решение транспортной задачи в среде Microsoft Exсel
Ввод исходных данных (в области C3:F6 – тарифы на перевозку продукции; в столбце G3:G6 – запасы; в ячейках С7, D7, E7, F7 – потребности).
В области решения в ячейке G10 введите формулу стоимости перевозок:
=СУММПРОИЗВ(C12:F15;C3:F6). Для этого необходимо нажать на значок f(x) на панели инструментов, выбрать математическую функцию СУММПРОИЗВ и ввести два массива C12:F15 и C3:F6. Далее в области C12:F15 проставьте любое первоначальное решение (например, единицы)/
В ячейке С16 записывается формула: =СУММ(C12:C14), т.е. сумма значений по столбцу (можно выделить значения столбца и нажать на знак автосуммы Σ на панели инструментов). Аналогично в D16, E16, F16. Автоматически суммируются значения по столбцам.
В ячейке G12 записывается формула: =СУММ(C12:F12), т.е. сумма значений по строке (можно выделить значения строки и нажать на знак автосуммы Σ на панели инструментов). Аналогично в G13, G14, G15. Автоматически суммируются значения по строкам:
Далее выполняют команду Поиск решения (вкладка СервисилиДанные).
Установить целевую ячейку G10, равной минимальному значению.
В поле ввода Изменяя ячейки установить C12:F15
В поле ввода Ограничения установить C12:F15 >= 0
C16:E16 = C7:E7
G12:G15= G3:G6
Далее нажимают на кнопку Параметры и устанавливают флажок на метод поиска сопряженных градиентов:
Вычисления производятся при нажатии кнопки Выполнитьдва раза. Получим решение задачи:
3.2.3. Обоснование ценовой стратегии
Решение
Определим нижнюю цену игры – α. Нижняя цена игры α — это максимальный выигрыш, который мы можем гарантировать себе, в игре против разумного противника, если на протяжении всей игры будем использовать одну и только одну стратегию (такая стратегия называется "чистой").
Найдем в каждой строке платежной матрицы минимальный элемент и запишем его в дополнительный столбец
Затем найдем максимальный элемент дополнительного столбца (отмечен звездочкой), это и будет нижняя цена игры.
| Стратегии "A" | Стратегии "B" | Минимумы строк | ||
| B1 | B2 | B3 | ||
| A1 | -1 | -1 | ||
| A2 | -2 | -2 | ||
| A3 | -1 | -1 | ||
| А4 | 1* | |||
В нашем случае нижняя цена игры равна: α = 1, и для того чтобы гарантировать себе выигрыш не хуже чем 1 мы должны придерживаться стратегии A4
Определим верхнюю цену игры - β
Верхняя цена игры β — это минимальный проигрыш, который может гарантировать себе игрок "В", в игре против разумного противника, если на протяжении всей игры он будет использовать одну и только одну стратегию.
Найдем в каждом столбце платежной матрицы максимальный элемент и запишем его в дополнительную строку снизу
Затем найдем минимальный элемент дополнительной строки (отмечен плюсом), это и будет верхняя цена игры.
| Стратегии "A" | Стратегии "B" | Минимумы строк | ||
| B1 | B2 | B3 | ||
| A1 | -1 | -1 | ||
| A2 | -2 | -2 | ||
| A3 | -1 | -1 | ||
| А4 | 1* | |||
| Максимумы столбцов | 1* |
В нашем случае верхняя цена игры равна: β = 1, и для того чтобы гарантировать себе проигрыш не хуже чем 1 противник ( игрок "B") должен придерживаться стратегии B2
Сравним нижнюю и верхнюю цены игры, в данной задаче они совпадают, т.е. α = β = 1 . Это значит, что игра имеет решение в так называемых "чистых", минимаксных стратегиях. Это как раз те стратегии для игроков "A" и "B" которые были найдены выше, при поиске нижней и верхней цен игры. То есть, в нашем случае для игрока "A" оптимальной будет стратегия A4, а для игрока "В" - B2. Нетрудно заметить, что элемент платежной матрицы расположенный на пересечении чистых оптимальных стратегий (строка 4, столбец 2) является одновременно минимальным в строке и максимальным в столбце. Такие элементы называются седловыми точками, именно их наличие и определяет существование решения игры в чистых стратегиях, а его значение (в нашем случае 1) совпадает с чистой ценой игры или просто ценой игры - v. Пара оптимальных стратегий, в играх имеющих седловую точку, всегда проходит через последнюю.
Ответ: Нижняя цена игры, верхняя цена игры и чистая цена игры: α = β = v = 1; Пара оптимальных стратегий: A4B2.
3.2.4. Обоснование распределения финансовых ресурсов между проектами.
На развитие трех предприятий выделено В млн. руб. Известна эффективность капитальных вложений xi в каждое j-е предприятие, заданная таблично значением нелинейной функции fj(xi), где 
, 
, n – количество предприятий, m – количество возможных сумм капитальных вложений.
Необходимо распределить выделенные средства между предприятиями таким образом, чтобы получить максимальный суммарный доход.
Исходные данные варианта 0:
| Объем капиталовложений xi (тыс. руб.) | Прирост выпуска продукции fj(xi) в зависимости от объема капиталовложений (тыс. руб.) | ||
| предприятие 1 | предприятие 2 | предприятие 3 | |
Математическая модель задачи.
Определить х* = (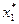 
, 
, …, 
, …, 
), обеспечивающий максимум целевой функции
и удовлетворяющий условиям
,
Математическая модель задачи варианта 0:
при ограничениях:
,
.
Условная оптимизация.
Максимально возможный доход, который может быть получен с предприятий (с k-го по n-е), определяется с помощью функции Беллмана:
,
где Сk – количество средств, инвестируемых в k-е предприятие, 0≤ Сk ≤ В.
На первом шаге условной оптимизации при k = n функция Беллмана представляет собой прибыль только с n-го предприятия. При этом на его инвестирование может остаться количество средств Сn, 0 ≤ Сn ≤ В. Чтобы получить максимум прибыли с этого предприятия, можно вложить в него все эти средства, т.е. Fn(Сn) = fn(Сn) и хn = Сn.
Для упрощения расчетов предполагаем, что распределение средств осуществляется в целых числах xi = {0, 100, 200, 300, 400, 500, 600, 700} тыс. руб.
Решение.
I этап. Условная оптимизация.
1-й шаг: k = 3.
Таблица 1
| x3 C3 | F3(C3) | 
| ||||||||
В шапке таблицы отражены варианты значений капиталовложений х3, которые могут быть предоставлены третьему предприятию. В столбце C3 отражены варианты значений капиталовложений, которые могут быть выделены всем трем предприятиям в совокупности.
Предположим, что все средства в количестве x3 = 700 тыс. руб. отданы третьему предприятию. В этом случае максимальный доход составит f3(x3) = 700 тыс. руб., следовательно: F3(C3) = f3(x3) и x3= C3.
2-й шаг: k = 2. Определяем оптимальную стратегию при распределении денежных средств между вторым и третьим предприятиями. При этом рекуррентное соотношение Беллмана имеет вид:
.
Представим в таблице расчет функции Беллмана.
Таблица 2
| x2 C2 | F2(C2) | 
| ||||||||
| 0+0 | ||||||||||
| 0+40 | 50+0 | |||||||||
| 0+50 | 50+40 | 70+0 | ||||||||
| 0+80 | 50+50 | 70+40 | 90+0 | |||||||
| 0+110 | 50+80 | 70+50 | 90+40 | 120+0 | 100/300 | |||||
| 0+150 | 50+110 | 70+80 | 90+50 | 120+40 | 160+0 | 100/400/500 | ||||
| 0+180 | 50+150 | 70+110 | 90+80 | 120+50 | 160+40 | 190+0 | 100/500 | |||
| 0+230 | 50+180 | 70+150 | 90+110 | 120+80 | 160+50 | 190+40 | 220+0 | 0/600 |
В шапке таблицы отражены варианты значений капиталовложений х2, которые могут быть предоставлены второму предприятию при условии, что часть средств выделяется третьему предприятию. В клетках таблицы первое слагаемое – это возможный прирост выпуска продукции второго предприятия f2(х2) в результате освоения капиталовложений х2; второе слагаемое – значение функции Беллмана, полученной на предыдущем шаге F3(C2 – х2), т.е. возможный прирост выпуска продукции третьего предприятия, если ему будет выделена оставшаяся часть капиталовложений, определяемая как C2 – х2.
Например, рассуждая формально, если при общей величине капиталовложений C2 = 0 второму предприятию выделяется х2 = 0, то прирост продукции составляет f2(0) = 0, а значение функции Беллмана из табл.1 составит: F3(0 – 0) = 0. Поэтому в клетке табл. 2 (0, 0) отражается сумма 0+0.
При общей величине капиталовложений C2 = 100 тыс. руб. возможны уже два варианта распределения средств между вторым и третьим предприятием:
1) второму предприятию ничего не выделяется, т.е. х2 = 0 и прирост продукции составляет f2(0) = 0. В этом случае значение функции Беллмана из табл. 1 составит F3(100 – 0) = F3(100) = 40 тыс. руб., т.е. вся сумма C2 = 100 тыс. руб. выделена третьему предприятию, поэтому суммарный прирост продукции составит 0+40, отражаемый в клетке (100, 0).
2) второму предприятию может быть выделено х2 = 100 тыс. руб., прирост продукции второго предприятия составляет f2(100) = 50 тыс. руб. В этом случае значение функции Беллмана из табл. 1 составит F3(100 – 100) = F3(0) = 0, т.е. вся сумма C2 = 100 тыс. руб. выделена второму предприятию, поэтому суммарный прирост продукции составит 50+0, отражаемый в клетке (100, 100).
Рассуждая аналогично, заполняются все строки табл. 2.
Максимальная сумма по каждой строке вносится в колонку F2(C2), одновременно в колонку вносят соответствующие максимальным суммам значения х2 из шапки табл. 2.
Например, в строке C2 = 100 максимальная сумма 160 не единственная, следовательно, F2(100) = 50, ему соответствует значение х2 = 100, следовательно, =100. В строке C2 = 500 максимальная сумма единственная 50, следовательно, F2(500) = 160, ему соответствуют значения х2 = 100, х2 = 400, х2 = 500, следовательно, =100/400/500.
3-й шаг: k = 1. Определяем оптимальную стратегию при распределении денежных средств между первым и двумя другими предприятиями, используя следующую формулу для расчета суммарного дохода:
,
на ее основе составлена табл. 3.
В шапке таблицы отражены варианты значений капиталовложений х1, которые могут быть предоставлены первому предприятию при условии, что часть средств выделяется второму и третьему предприятию. В клетках таблицы первое слагаемое – это возможный прирост выпуска продукции первого предприятия f1(х1) в результате освоения капиталовложений х1; второе слагаемое – значение функции Беллмана, полученной на предыдущем шаге F2(C1–х1), т.е. возможный прирост выпуска продукции второго и третьего предприятий, если им будет выделена оставшаяся часть капиталовложений, определяемая как C1 – х1.
Таблица 3
| x1 C1 | F1(C1) | 
| ||||||||
| 0+0 | ||||||||||
| 0+50 | 30+0 | |||||||||
| 0+90 | 30+50 | 50+0 | ||||||||
| 0+110 | 30+90 | 50+50 | 70+0 | |||||||
| 0+130 | 30+110 | 50+90 | 70+50 | 100+0 | 100/200 | |||||
| 0+160 | 30+130 | 50+110 | 70+90 | 100+50 | 150+0 | 0/100/200/300 | ||||
| 0+200 | 30+160 | 50+130 | 70+110 | 100+90 | 150+50 | 190+0 | 100/500 | |||
| 0+230 | 30+200 | 50+160 | 70+130 | 100+110 | 150+90 | 190+50 | 210+0 | 500/600 |
Значение функции Беллмана F1(С1) представляет собой максимально возможный доход со всех предприятий, а значение 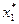, на котором достигается максимум дохода, является оптимальным количеством средств, вложенных в первое предприятие.
Значение целевой функции равно максимальному значению функции Беллмана F1(С1) из табл. 3.
Следовательно, значение целевой функции равно Fmax(x*) = 240 тыс. руб.
II этап. Безусловная оптимизация.
Далее на этапе безусловной оптимизации для всех последующих шагов вычисляется величина Сk = (Сk-1 – хk-1) оптимальным управлением на k-м шаге является то значение хk, которое обеспечивает максимум дохода при соответствующем состоянии системы Sk.
Определяем компоненты оптимальной стратегии. Для этого значения функций Беллмана и соответствующие им оптимальные значения х вносим в итоговую табл. 4.
Таблица 4.
| C1 | F3(C3) |
| F2(C2) |
| F1(C1) |
|
| 100/300 | 100/200 | |||||
| 100/400/500 | 0/100/200/300 | |||||
| 100/500 | 100/500 | |||||
| 0/600 | 500/600 |
1-й шаг. По данным из табл. 4 максимальный доход при распределении 700 тыс. руб. между тремя предприятиями составляет: C1 = 700, F1(700) = 240 тыс. руб.
При этом возможны следующие варианты.
Первому предприятию нужно выделить:
1) 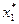= 500 тыс. руб.;
2) 
= 600 тыс. руб.
2-й шаг. Определяем величину оставшихся денежных средств, приходящуюся на долю второго и третьего предприятий:
1) С2 = C1 – 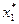= 700 – 500 = 200 тыс. руб.;
2) С2 = C1 – = 700 – 600 = 100 тыс. руб.
По данным табл. 4 находим, что оптимальный вариант распределения между вторым и третьим предприятиями денежных средств размером:
1) 200 тыс. руб. составляет: F2(200) = 90 тыс. руб. при выделении второму предприятию = 100 тыс. руб.;
2) 100 тыс. руб. составляет: F2(100) = 50 тыс. руб. при выделении второму предприятию 
= 100 тыс. руб.
3-й шаг. Определяем величину оставшихся денежных средств, приходящуюся на долю третьего предприятия:
1) С3 = C2 – = 200 – 100 = 100 тыс. руб.;
2) С3 = C2 – = 200 – 200 = 0.
По данным табл. 4 находим:
1) F3(100) = 40 и 
= 100 тыс. руб.;
2) F3(0) = 0 и = 0.
Таким образом, возможны два альтернативных варианта оптимального плана инвестирования предприятий:
1) х* = (500, 100, 100), который обеспечит максимальный доход, равный
F(700) = f1(500) + f2(100) + f3(100) = 150 + 50 + 40 = 240 тыс. руб.;
2) х** = (600, 100, 0), который обеспечит максимальный доход, равный
F(700) = f1(600) + f2(100) + f3(0) = 190 + 50 + 0 = 240 тыс. руб.
Оформление пояснительной записки
Курсовая работа оформляется на листах формата А4, общим объемом 35-40 страниц. Оформление контрольно-курсовой работы должно соответствовать требованиям ГОСТ 7.32-2001. Оформленная работа должна содержать титульный лист, содержание, основную часть, заключение с общими выводами.
К работе должны быть приложены отчеты о решении задач в среде Microsoft Excel.
Форма титульного листа контрольно-курсовой работы представлена в приложении А.
Дата: 2016-10-02, просмотров: 204.
