Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Алгоритм цифровой подписи DSA (Digital Signature Algorithm) предложен в 1991 г. в НИСТ США для использования в стандарте цифровой подписи DSS (Digital Signature Standard). Алгоритм DSA является развитием алгоритмов цифровой подписи Эль Гамаля и К.Шнорра.

Отправитель и получатель электронного документа используют при вычислении большие целые числа: G и P – простые числа, L бит каждое (512 £ L £ 1024); q – простое число длиной 160 бит (делитель числа (P –1)). Числа G, P, q являются открытыми и могут быть общими для всех пользователей сети.

Отправитель выбирает случайное целое число X, 1< X< q. Число X является секретным ключом отправителя для формирования электронной цифровой подписи.

Затем отправитель вычисляет значение

Y = G^X mod P.

Число Y является открытым ключом для проверки подписи отправителя. Число Y передается всем получателям документов.

Этот алгоритм также предусматривает использование односторонней функции хэширования h(·). В стандарте DSS определен алгоритм безопасного хэширования SHA (Secure Hash Algorithm).

Для того чтобы подписать документ M, отправитель хэширует его в целое хэш-значение m:

m = h(M), 1< m < q,

затем генерирует случайное целое число K, 1< K< q, и вычисляет число r:

r = (G^K mod P) mod q.

Затем отправитель вычисляет с помощью секретного ключа X целое число s:

s = 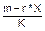mod q.

Пара чисел r и s образует цифровую подпись

S = (r ,s)

под документом M.

Таким образом, подписанное сообщение представляет собой тройку чисел [M, r, s].

Получатель подписанного сообщения [M, r, s] проверяет выполнение условий

0 < r < q, 0 < s < q

и отвергает подпись, если хотя бы одно из этих условий не выполнено.

Затем получатель вычисляет значение

w = mod q,

хэш-значение

m = h(M)

и числа

u₁ = (m * w) mod q,

u₂ = (r * w) mod q.

Далее получатель с помощью открытого ключа Y вычисляет значение

v = (( ) mod P) mod q

и проверяет выполнение условия

v = r.

Если условие v = r выполняется, тогда подпись

S = (r,s) под документом M признается получателем подлинной.

Можно строго математически доказать, что последнее равенство будет выполняться тогда, и только тогда, когда подпись S = (r,s) под документом M получена с помощью именно того секретного ключа X, из которого был получен открытый ключ Y. Таким образом, можно надежно удостовериться, что отправитель сообщения владеет именно данным секретным ключом X (не раскрывая при этом значения ключа X) и что отправитель подписал именно данный документ M.

По сравнению с алгоритмом цифровой подписи Эль Гамаля алгоритм DSA имеет следующие основные преимущества:

1. При любом допустимом уровне стойкости, т.е. при любой паре чисел G и P (от 512 до 1024 бит), числа q, X, r, s имеют длину по 160 бит, сокращая длину подписи до 320 бит.

2. Большинство операций с числами K, r, s, X при вычислении подписи производится по модулю числа q длиной 160 бит, что сокращает время вычисления подписи.

3. При проверке подписи большинство операций с числами u₁, u₂, v, w также производится по модулю числа q длиной 160 бит, что сокращает объем памяти и время вычисления.

Недостатком алгоритма DSA является то, что при подписывании и при проверке подписи приходится выполнять сложные операции деления по модулю q:

s = 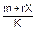(mod q), w = 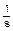(mod q),

что не позволяет получать максимальное быстродействие.

Следует отметить, что реальное исполнение алгоритма DSA может быть ускорено с помощью выполнения предварительных вычислений. Заметим, что значение r не зависит от сообщения M и его хэш-значения m. Можно заранее создать строку случайных значений K и затем для каждого из этих значений вычислить значения r. Можно также заранее вычислить обратные значения K^–1 для каждого из значений K. Затем, при поступлении сообщения M, можно вычислить значение s для данных значений r и K^–1. Эти предварительные вычисления значительно ускоряют работу алгоритма DSA.