Метод деления отрезка пополам (известный еще и как метод половинного деления) также является рекурсивным, т.е. предусматривает повторение с учетом полученных результатов.
Исходные данные к методу деления отрезка пополам:
- дана функция f(x);
- определена допустимая погрешность Q;
- определен некоторый интервал [a,b], содержащий решение уравнения.
Алгоритм нахождения корня:
1. Вычисляем значение координаты x, беря середину отрезка [a,b], т.е. x= (a+b)/2
2. Вычисляем значения f(a), f(b), f(x), и осуществляем следующую проверку:
Если |f(x)| <= Q, то корень с указанной точностью найден.
Если |f(x)| > Q, т.е. необходимая точность еще не достигнута, то формируем два интервала: [a,x] и [x,b] проверяем знаки f(a), f(b), f(x). На концах одного из этих интервалов знаки функции будут одинаковы, а на другом – различны. Именно тот интервал, на концах которого знаки различны, мы берем за основу при следующей итерации, т.е. приравниваем либо a, либо b к х.
3. Переходим к пункту 1.
Рис. 9. Метод деления отрезка пополам
Метод хорд
Исходные данные к методу деления отрезка пополам:
- дана функция F(x);
- определена допустимая погрешность Q;
- определен некоторый интервал [a,b], содержащий решение уравнения.
Алгоритм нахождения корня:
1. Строим хорду, проходящую через точки f(a) и f(b) и вычисляем точку пересечения (x) хорды с осью абсцисс.
Формула прямой, проходящей через точки а и в, т.е. хорды:
y=k*x+y0, где
k =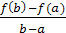 
y0 = 
тогда точка х пересечения хорды с осью абсцисс будет вычисляться по формуле:
x = 
2. Вычисляем значения f(a), f(b), f(x), и осуществляем следующую проверку:
Если |f(x)| <= Q или длина отрезка [a,b] <= Q, то корень с указанной точностью найден.
Если |f(x)| > Q, т.е. необходимая точность еще не достигнута, то формируем два интервала: [a,x] и [x,b] проверяем знаки F(a), F(b), F(x). На концах одного из этих интервалов знаки функции будут одинаковы, а на другом – различны. Именно то интервал, на концах которого знаки различны, мы берем за основу при следующей итерации, т.е. приравниваем либо a, либо b к х.
3. Переходим к пункту 1.
Рис. 10. Метод хорд
Вычисление интеграла
Известно, что определенный интеграл функции f(x) типа на интервале [a,b] численно представляет собой площадь криволинейной трапеции ограниченной прямыми x=0, y=a, y=b и функцией y=f(x) (рис. 11). Есть два метода вычисления этой площади или определенного интеграла — метод трапеций (Рис. 2) и метод средних прямоугольников (Рис. 3).
Рис. 11. Криволинейная трапеция
По методам трапеций и средних прямоугольников соответственно интеграл равен сумме площадей прямоугольных трапеций (рис. 12) или сумме площадей прямоугольников (рис. 13), в которых высота определяется по точке пересечения верхнего основания прямоугольника, которое график функции должен пересекать в середине. Соответственно получаем формулы площадей
для метода трапеций:
Рис. 12. Метод трапеций
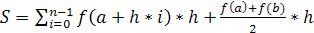, где h – длина отрезка, n – число отрезков
и для метода средних прямоугольников:
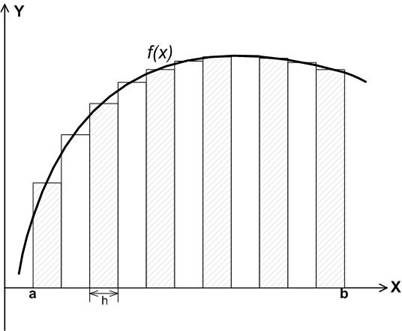
Рис. 13. Метод средних прямоугольников
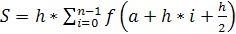, где h – длина отрезка, n – число отрезков
Алгоритм вычисления интеграла по любому из методов будет выглядеть следующим образом:
- При заданном числе отрезков разбиения вычисляется (по заданному методу) первоначальное приближение S0
- Число отрезков разбиения увеличивается на k (например, k=5) и вычисляется новое значение интеграла S1
- Если |S0-S1| <= заданной точности, то за точное значение интеграла принимается значение S1
В противном случае за первоначальное приближение S0 принимается значение S1 и алгоритм повторяется, начиная с п.2
Содержание отчета
Отчет по лабораторной работе должен содержать:
- задание лабораторной работы, соответствующее варианту
- структурную схему алгоритма программы и подпрограммы (подпрограмм)
- текст программы
- результаты работы программы
Лабораторная работа 14
Цель работы
Закрепление пройденного материала: основные элементы языка Си, массивы, условные операторы, функции, стандартные библиотеки.
Задание
Разработать программу и подпрограмму (подпрограммы) построения графика функции на экране в виде последовательности точек и в выходном файле в виде гистограммы.
При выводе графика функции на экран ось Xрасположить горизонтально (количество позиций по оси X = 78), а ось Y– вертикально (количество позиций по оси Y = 25).
При выводе графика функции в выходной файл ось Xрасположить вертикально (количество позиций по оси X = 60), а ось Y– горизонтально (количество позиций по оси Y = 80), каждый столбец гистограммы пометить значением функции. После гистограммы вывести масштаб функции по оси Y.
Функция и координаты отрезка приведены в таблице.
| № | Функция | Границы отрезка |
| у = ê2*sin(x)ê- êcos(3*x)ê | -p/2 ¸ p | |
| y = 2*sin(x) + 3*cos(2*x) | -p/2 ¸ p/2 | |
| y = (x-3)/(x2 + 2) | -1 ¸ 4 | |
| y = x2 * exp(-x) | -1 ¸ 2 | |
| y = exp(-x) * sin(2x) | -p/2 ¸ 2p | |
| y = (x+2)2/3 - (x-2)2/3 | -3 ¸ 2.5 |
Рекомендации по выполнению лабораторной работы
При выполнении даннной лабораторной работы необходимо учитывать следующее:
- Графики функций, выводимые на экран, должны быть отмасштабированы в соответствии с заданными диапазонами (количество позиций по оси X и количество позиций по оси/Y) и на каждом графике должны быть отображены оси X и Y.
В связи с этим можно предложить следующие варианты масштабирования функций:
a) Пусть ymax и ymin – максимальное и минимальное значения функции, график которой должен быть построен, а xmin и xmax – границы отрезка по оси Х.
В зависимости от вида функции возможны следующие случаи расчета масштаба функции:
График функции имеет вид, приведенный на рис. 14
Рис. 14. График функции (вариант 1)
В этом случае диапазон изменения х будет хmin=0 - xmax, а диапазон изменения функции - ymin и ymax.
График функции имеет вид, приведенный на рис. 15
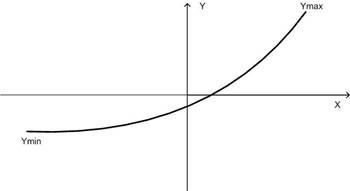
Рис. 15. График функции (вариант 2)
В этом случае диапазон изменения х будет xmin - xmax, а диапазон изменения функции - ymin и ymax.
График функции имеет вид, приведенный на рис. 16
Рис. 16. График функции (вариант 3)
В этом случае диапазон изменения х будет хmin =0 - xmax, а диапазон изменения функции - ymin=0 и ymax.
График функции имеет вид, приведенный на рис. 17
Рис. 17. График функции (вариант 4)
В этом случае диапазон изменения х будет хmin=0 - xmax, а диапазон изменения функции - ymin и ymax=0.
Значения границ отрезка по оси Х и значений ymin и ymax для расположения графика функции в других квадрантах получаются аналогично.
b) Масштаб функции по оси Y рассчитывается как my = (ymax-ymin)/<диапазон_по_Y>, а шаг изменения аргумента х – как dx = (xmax-хmin)/ <диапазон_по_X>
- На основании полученных масштабов строятся требуемые графики функций и оси координат.
График функции, построенный на экране, должен иметь вид, аналогичный приведенному на рис. 18 (с точностью до функции и символов, используемых для обозначения точек функции). Значения по осям X и Y можно не указывать.
Рис. 18. Вид графика на экране
График функции в виде гистограммы должен иметь вид, аналогичный приведенному на рис. 19 (с точностью до функции и символов, используемых для обозначения точек функции). Значения по осям X и Y можно не указывать. На гистограмме ОБЯЗАТЕЛЬНО должны быть указаны значения функции для соответствующих "столбиков" и в тех позициях, как показано на рисунке. Количество символов после десятичной точки для значений функции на гистограмме должно быть не меньше 3. Символы для построения гистограммы выбираются произвольно.
!!! После гистограммы должен быть выведен масштаб функции по оси Y !!!
Рис. 19. График в виде гистограммы
Содержание отчета
Отчет по лабораторной работе должен содержать:
- задание лабораторной работы, соответствующее варианту
- структурную схему алгоритма программы и подпрограммы (подпрограмм)
- текст программы
- результаты работы программы.
Дата: 2016-10-02, просмотров: 238.
