Задание № 4 содержит 5 задач для 25 вариантов. Каждый студент решает одну задачу в соответствии со своим вариантом.
Задача №1
Тонкая пластина из пластика толщиной 2δ = 6 мм с размерами 2х3м2, с начальной температурой tн погружается в горячую среду с температурой tж = 100 оС.
Коэффициент теплопроводности (λ), теплоемкость (с), плотность (ρ) для материала пластины, а также постоянный коэффициент теплоотдачи в процессе нагрева (α) и другие данные, необходимые для расчета, приведены в табл.10 по вариантам.а=λ/сρ
Определить температуру в центре (tц) и на поверхности (tп) пластины через время τ1 после погружения пластины в горячую среду.
Изобразить график распределения температуры по толщине пластины для моментов времени τ=0, τ= τ1, τ=∞.
Определить полное количество тепла, воспринятого пластиной в процессе нагрева (Qп, Дж). Ответы выделить.
Таблица10
| № вар | |||||
| λз, Вт/м· К | 1.2 | 1,4 | 1,6 | 1,8 | |
| С, Дж/кг К | |||||
| ρ, кг/м3 | |||||
| α, Вт/(м2 К) | |||||
| tн ,оC | |||||
| τ1, с |
Задача № 2
Длинный стальной вал диаметром d=40 мм с начальной температурой tн погружается в воду с температурой tж.
Свойства стали: теплопроводность λ = 40 Вт/мК. Теплоемкость с = 460 Дж/(кг·К), плотность ρ = 7900 кг/м3.
Коэффициент теплоотдачи в процессе охлаждения (α) и другие данные, необходимые для расчета, приведены в табл. 11 по вариантам.
Определить температуры в центре (tц) и на поверхности (tп) вала время (τ1) после его погружения в холодную воду.
Изобразить график распределения температуры по диаметру вала для моментов времени τ=0, τ= τ1, τ1=∞.
Определить полное количество тепла (Qп, Дж/м), отданное валом в процессе охлаждения, в расчете l=1м его длины. Ответы выделить.
Таблица 11
| № вар | |||||
| tн оC | |||||
| tж оC | |||||
| α, Вт/(м2 К) | |||||
| τ1, мин | 1,8 |
Задача № 3
Длинный металлический стержень диаметром d=50 мм с начальной температурой tн помещен с температурой tж для термической обработки.
Коэффициент теплопроводности (λ), удельная теплоемкость (с), плотность (ρ) материала стержня, коэффициент теплоотдачи (α) и другие исходные данные, необходимые для расчета, приведены в табл.12 по вариантам.
Сколько времени (τ1, сек) стержень должен оставаться в печи. Чтобы температура в центре стержня (tц) достигла заданной величины? Какую температуру в этот момент времени будет иметь поверхность стержня (tп)?
Изобразить график распределения температуры по диаметру вала для моментов времени τ=0, τ= τ1, τ1=∞.
Определить полное количество тепла (Qп,Дж/м), отданное валом в процессе охлаждения, в расчете на l=1м его длины. Ответы выделить.
Таблица 12
| № вар | |||||
| tн , оC | |||||
| tж , оC | |||||
| λ, Вт/(м К) | |||||
| с, Дж/(кг К) | |||||
| ρ, кг/м3 | |||||
| α, Вт/(м2 К) | |||||
| tц , оC |
Задача№ 4
Нагретый шаровой калориметр из меди диаметром d=50мм с начальной температурой tн помещен в воду с температурой tж.
Свойства меди: коэффициент теплопроводности λ=384 Вт/(м К), удельная теплоемкость с=381 Дж/(кг К), плотность ρ=8800 кг/м3.
Коэффициент теплоотдачи поверхности шара в процессе охлаждения (α) и другие исходные данные приведены в табл. 13 по вариантам.
Определить температуры в центре (tц) и на поверхности шара (tп) через время (τ1) после погружения его в воду.
Изобразить график распределения температуры по диаметру вала для моментов времени τ=0, τ= τ1, τ1=∞.
Определить полное количество тепла (Qп, Дж), отданное шаровым калориметром в процессе его охлаждения. Ответы выделить.
Таблица 13
| № вар | |||||
| tн , оC | |||||
| tж , оC | |||||
| α, Вт/(м2 К) | |||||
| τ1, с | 8,2 | 10,9 | 13,6 | 5,5 | 27,3 |
Задача № 5
Шаровой калориметр из мрамора диаметром d=50 мм с начальной температурой tн охлаждается на открытом воздухе с температурой tж.
Свойства мрамора: коэффициент теплопроводности λ=3,5 Вт/(м К), удельная теплоемкость с=920 Дж/(кг К), плотность ρ=2800 кг/м3.
Постоянный коэффициент теплоотдачи в процессе охлаждения (α) и другие исходные данные приведены в табл. 14 по вариантам.
Определить, через какое время (τ1,с) температура в центре шарового калориметра (tц) достигнет заданного значения. Какая температура в этот момент времени будет на поверхности шарового калориметра (tп)?
Изобразить график распределения температуры по диаметру вала для моментов времени τ=0, τ= τ1, τ1=∞.
Определить полное количество тепла (Qп, Дж), отданное шаровым калориметром в процессе его охлаждения.
Таблица5
| № вар | |||||
| tн ,оC | |||||
| tж ,оC | |||||
| α, Вт/(м2 К) | 9,8 | 8,4 | 5,6 | ||
| tц,, с | 25,7 | 24,2 | 37,7 |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Поясните, почему циклы в тепловых двигателях совершаются в направлении по часовой стрелке, а в холодильных машинах – против часовой стрелки?
2. Покажите идеальный цикл Карно холодильной машины T-s-диаграмме. Дайте понятие холодильного коэффициента. Как рассчитать холодильный коэффициент цикла Карно?
3. Приведите схему и цикл p-v диаграмме воздушной холодильной установки. Нанесите на схему узловые точки цикла. Какими площадями в p-v диаграмме характеризуются: а) работа, затрачиваемая на компрессор (lк), б) работа, получаемая в детандере (lD), в) результирующая работа цикла (l)?
4. Приведите цикл воздушной холодильной установки в T-s-диаграмме. Укажите, в каких узлах установки совершаются процессы цикла. Поясните физический смысл холодильного коэффициента цикла (ε), приведите формулу для его расчета.
5. Приведите цикл воздушной холодильной установки в T-s-диаграмме. Обозначьте температуру вырабатываемого холода (Тх) и температуру окружающей среды (Тос). Покажите цикл Карно для данного интервала температур. Сравните по удельной холодопроизводительности (qx) и затрачиваемой работе (l) обратимый цикл воздушной холодильной установки и цикл Карно, сделайте выводы.
6. Приведите схему и цикл парокомпрессионной холодильной установки в T-s-диаграмме. Нанесите узловые точки на схему. Какими площадями в T-s-диаграмме характеризуются: а) удельная холодопроизводительность (qx), б) теплота, отводимая в конденсаторе (q0)?
7. Приведите цикл парокомпрессионной холодильной установки в T-s-диаграмме. Укажите, в каких узлах установки совершаются процессы цикла. Поясните физический смысл холодильного коэффициента цикла (ε). Приведите формулу для его расчета.
8. В учебнике [1] с. 378 на рис. 3-10 приведен цикл парокомпрессионной холодильной установки. Как изменится удельная холодопроизводительность цикла (qx), если хладоагент испарять полностью до х3 = 1? Приведите такой цикл в T-s-диаграмме. Сделайте выводы.
9. В учебнике [1] с. 378 на рис. 3-10, приведен цикл парокомпрессионной холодильной установки. Сравните по удельной холодопроизводительности (qx) обратимый цикл этой установки и идеальный цикл Карно для данного интервала температур. Покажите площади, которыми характеризуется удельная холодопроизводительность (qx) этих циклов.
10. Возможно ли осуществить изотермические процессы подвода и отвода тепла в циклах: а) парокомпрессионной холодильной установки, б) воздушной холодильной установки?
11. Каково назначение теплового насоса? Дайте понятие отопительного коэффициента. Как вычислить отопительный коэффициент идеального цикла Карно?
12. Каков механизм передачи тепла теплопроводностью в газах? От каких факторов зависит коэффициент теплопроводности газов? Сравните коэффициенты теплопроводности легких и тяжелых газов.
13. Каков механизм передачи тепла теплопроводностью в металлах? Как зависит коэффициент теплопроводности от температуры для чистых металлов, для сплавов?
14. От каких факторов зависит коэффициент теплопроводности строительных и теплоизоляционных материалов? В каких пределах он изменяется? Приведите значения коэффициентов теплопроводности для кирпича, стекловаты, асбеста [4, с.401, табл.3].
15. Каков механизм передачи тепла теплопроводностью в жидкостях? От каких факторов зависит коэффициент теплопроводности жидкостей? Приведите пределы изменения λ для жидкостей.
16. Дайте понятие коэффициента температуропроводности. Как он обозначается, какую имеет размерность, что характеризует, от каких факторов зависит? Рассчитайте коэффициент температуропроводности для шлакобетона и льда при t=00C. Воспользуйтесь [4, с.401-402, табл.3].
17. Дайте понятие температурного поля. Приведите практические примеры температурных полей: 1) стационарного одномерного, 2) нестационарного одномерного, 3) стационарного трехмерного, 4) нестационарного двухмерного.
18. Дайте полную характеристику дифференциального уравнения 1.27 [4, с.19], поясните все величины, входящие в уравнение; укажите, какие процессы передачи тепла и в каких телах описывает данное уравнение.
19. Какие процессы передачи тепла и в каких телах описывает уравнение 1.27 [4, с.19]? Запишите это уравнение для стационарной теплопроводности в телах: а) с внутренними источниками тепла, б) без внутренних источников тепла. Приведите примеры таких процессов.
20. Что включают в себя условия однозначности? Для чего они нужны?
21. Как формируются граничные условия первого, второго и третьего рода? Для чего они присоединяются к дифференциальному уравнению?
22. Приведите математическое выражение закона Фурье: а) для теплового потока Q Вт, б) для плотности теплового потока q, Вт/м2. Какой способ передачи тепла описывает закон Фурье? Чем объяснить знак (-) в правой части уравнения Фурье?
23. Дайте понятие изотермической поверхности. Могут ли две изотермические поверхности пересекаться? Какое направление называется нормалью к изотермической поверхности? Сравните между собой градиенты температуры по нормали и по любому другому направлению к изотермической поверхности.
24. Что описывают уравнения (2.3) и (2.4), приведенные в [4, с.25]? Что рассчитывается по уравнениям (2.7) и (2.9)? Запишите указанные уравнения, дайте все пояснения, приведите рисунок.
25. Что рассчитывается по уравнению (2.22), приведенному в [4, с.30]? Как называются слагаемые знаменателя этого уравнения и как они связаны с перепадами температур (tж1-tс1), (tс1-tс2), (tс2-tж2)? Дайте понятие коэффициента теплопередачи плоской стенки. Запишите все уравнения с пояснениями, приведите рисунок.
26. Запишите уравнение, по которому можно рассчитать плотность теплового потока, q (Вт/м2), передаваемого от среды с температурой tж1 в среду с температурой tж2 через трехслойную плоскую стенку. Приведите график перепадов температур для условия: α1>>α2, λ1>>λ2, λ1>>λ2, λ2>>λ3.
27. Что описывают уравнения (2.35) и (2.36). приведенные в [4, с.33]? Что рассчитывается по уравнениям (2.39) и (2.40)? Запишите указанные уравнения, дайте все пояснения, приведите рисунок.
28. Что рассчитывается по уравнению (2.49), приведенному в [4, с.36]? Запишите уравнение с пояснением, приведите рисунок. Можно ли расчет теплопередачи через цилиндрическую стенку производить по уравнению для плоской стенки?
29. Запишите уравнение, по которому можно рассчитать линейную плотность теплового потока (ql, Вт/м), передаваемого от горячей воды с температурой tж1 к окружающему воздуху с температурой tж2 через стенку трубы, покрытой одним слоем тепловой изоляции. Приведите график перепадов температур для условия α1>>α2, λтр>>λиз.
30. Дайте понятие критического диаметра изоляции. Как изменятся теплопотери (Q, Вт), если наложить изоляцию на трубу, наружный диаметр которой: а) d2< dкр, б) d2=dкр, в) d2>d кр?
31. Что описывают уравнения (2.61) и (2.62), приведенные в [4, с.40]?Что рассчитывается по уравнениям (2.64) и (2.65)? Запишите указанные уравнения, дайте все пояснения, приведите рисунок.
32. Что рассчитывается по уравнению (2.66), приведенному в [4, с.41]? Запишите уравнение с пояснением, приведите рисунок.
33. Что рассчитывается по уравнениям (2.90) и (2.87), приведенным в [4, с.49-50]? Поясните все величины, входящие в уравнения, приведите рисунок.
34. Что рассчитывается по уравнению (2.85), приведенному в [4, с.41]? Запишите это уравнение и поясните все величины его правой части. Дайте рисунок с расстановкой размеров.
35. Какими способами можно увеличить тепловой поток Q, Вт, передаваемый через стенку от среды с температурой tж1 к среде с температурой tж2 при условии, что α1>>α2?
36. Приведите примеры тел и систем с внутренними источниками тепла. Поясните смысл величины qv, Вт/м3. Рассчитайте значение qv для проводника электрического тока диаметром d= 5 мм, длиной l= 10 м при напряжении U= 220В и силе тока I = 2А.
37. Что описывают уравнения (2.133) и (2.134), приведенные в [4, с.59]? Что рассчитывается по уравнениям (2.137), (1.138), (2.141)? Запишите указанные уравнения, дайте необходимые пояснения, приведите рисунок.
38. Что описывают уравнения (2.143) и (2.144), приведенные [4, с.61]? Что рассчитывается по уравнениям (2.147), (2.147), (2.148)? Запишите указанные уравнения, дайте необходимые пояснения, приведите рисунок.
39. Что рассчитывается по уравнению (2.153), приведенному в [4, с.64]? Запишите уравнение, приведите рисунок. Напишите ошибки в уравнении (2.158) и запишите его правильно.
40. Что рассчитывается по уравнению (2.159), приведенному [4, с.64]? Запишите уравнение, приведите рисунок. Запишите уравнения для расчета температур на поверхностях стенки tс1 и tс2.
41. В учебнике [4] рассматриваются следующие классические задачи стационарной теплопроводности с внутренним тепловыделением: 1. Пластина при симметричных условиях охлаждения. Перечислите еще 4 задачи.
42. Стационарное температурное поле цилиндрического стержня и трубы с внутренними источниками тепла описывается одинаковым дифференциальным уравнением. Запишите это уравнение. На примере цилиндрического стержня поясните физический смысл граничных условий.
43. В учебнике [4, с.59 рис. 2.24,] показано температурное поле пластины с внутренним тепловыделением при симметрических условиях охлаждения (α, tж). Покажите график изменения температуры по толщине пластины для условия α1>α2, tж1=tж2.
44. При математическом описании процессов теплопроводности цилиндрического стержня и трубы с внутренними источниками тепла применяются уравнения:
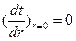 ,
,  ,
, 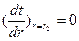 ,
, 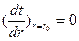
45. Поясните физический смысл уравнений.
46. Для цилиндрического стержня с внутренним тепловыделением дано:qv, l, d . Как рассчитать: а) тепловой поток (Q, Вт), рассеиваемый поверхностью охлаждения стержня, б) плотность теплового потока (q, Вт/м2), рассеиваемого с 1м2 поверхности охлаждения?
47. Для цилиндрической стенки (трубы) с внутренним тепловыделением и охлаждением по наружной поверхности дано:qv, r1, r2, l. Как рассчитать: а) тепловой поток (Q, Вт), рассеиваемый поверхностью охлаждения трубы, б) плотность теплового потока (q, Вт/м2), рассеиваемого с 1м2 поверхности охлаждения?
КОНТРОЛЬНАЯ РАБОТА № 3
ЗАДАНИЕ № 1
Дата: 2016-10-02, просмотров: 439.