1. Кусочно-линейная функция. Данная функция возникает как комбинация нескольких линейных производственных функций (т.е. технологий производства), каждая из которых используется на своем интервале. И для каждой комбинации факторов производства фирма выбирает ту технологию, которая дает наибольший выпуск :

Производственная функция характеризует зависимость между количеством используемых ресурсов (факторов производства) и максимально возможным объемом выпуска, который может быть достигнут при условии, что все имеющиеся ресурсы используются наиболее рациональным образом.

Производственная функция обладает следующими свойствами:

1. Существует предел увеличения производства, который может быть достигнут при увеличении одного ресурса и постоянстве прочих ресурсов. Если, например, в сельском хозяйстве увеличивать количество труда при постоянных количествах капитала и земли, то рано или поздно наступает момент, когда выпуск перестает расти.

2. Ресурсы дополняют друг друга, но в определенных пределах возможна и их взаимозаменяемость без сокращения выпуска. Ручной труд, например, может заменяться использованием большего количества машин, и наоборот.

3. Чем длиннее временной период, тем большее количество ресурсов может быть пересмотрено. В этой связи различают мгновенный, короткий и длительный периоды.Мгновенный период —период, когда все ресурсы являются фиксированными.Короткий период — период, когда, по крайней мере, один ресурс является фиксированным.Длительный период - период, когда все ресурсы являются переменными.

Обычно в микроэкономике анализируется двухфакторная производственная функция, отражающая зависимость выпуска (q) от количества используемых труда ( ) и капитала ( ). Напомним, что под капиталом понимаются средства производства, т.е. количество машин и оборудования, используемое в производстве и измеряемое в машино-часах (тема 2, п. 2.2). В свою очередь количество труда измеряется в человеко-часах.

Как правило, рассматриваемая производственная функция выглядит так:

A, α, β — заданные параметры. ПараметрА — это коэффициент совокупной производительности факторов производства. Он отражает влияние технического прогресса на производство: если производитель внедряет передовые технологии, величинаА возрастает, т.е. выпуск увеличивается при прежних количествах труда и капитала. Параметры α и β — это коэффициенты эластичности выпуска соответственно по капиталу и труду. Иными словами, они показывают, на сколько процентов изменяется выпуск при изменении капитала (труда) на один процент. Коэффициенты эти положительны, но меньше единицы. Последнее означает, что при росте труда при постоянном капитале (либо капитала при постоянном труде) на один процент производство возрастает в меньшей степени.

Функция Кобба — Дугласа — зависимость объёма производства от создающих его факторов производства — затрат труда и капитала .

Впервые была предложена Кнутом Викселлем. В 1928 году функция проверена на статистических данных Чарльзом Коббом (англ. Charles Cobb) и Полом Дугласом (англ. Paul Douglas) в работе «Теория производства». В этой статье была предпринята попытка эмпирическим путем определить влияние затрачиваемого капитала и труда на объём выпускаемой продукции в обрабатывающей промышленности США.

Общий вид функции:

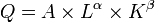
Где А — технологический коэффициент, α — коэффициент эластичности по труду, а β — коэффициент эластичности по капиталу.

Если сумма показателей степени (α + β) равна единице, то функция Кобба — Дугласа является линейно однородной, то есть она демонстрирует постоянную отдачу при изменении масштабов производства.

Если сумма показателей степени больше единицы, функция отражает возрастающую отдачу, а если она меньше единицы, — убывающую. Изокванта, соответствующая функции Кобба — Дугласа, будет выпуклой и «гладкой»

Впервые производственная функция была рассчитана в 1920-е годы для обрабатывающей промышленности США, в виде равенства

Обобщением функции Кобба — Дугласа является функция с постоянной эластичностью замещения факторов (CES функция): , которая соответствует функции Кобба — Дугласа при .

ФУНКЦИЯ ПРОИЗВОДСТВЕННАЯ С ПОСТОЯННОЙ ЭЛАСТИЧНОСТЬЮ ЗАМЕЩЕНИЯ - Это линейно однородная производственная функция с постоянной эластичностью замещения ресурсов.(Словарь современной экономической теории Макмиллана.-М., 1997) Эластичность может принимать значения, не равные единице. Функция имеет следующий вид: Q = A [a K-b + (1 - c) L-b]-1/b, где Q - объем производства; K и L - капитал и труд соответственно; а, b и с - константы. Это понятие было впервые сформулировано К.Дж. Эрроу, Х.Б. Ченери, Б.С. Минасом и Р.М. Солоу в работе "Замещение капитал-труд и экономическая эффективность".(Словарь современной экономической теории Макмиллана.-М., 1997) См. также: Соотношение капитал-труд

Еще одна производственная функция — функция Леонтьева. Она предполагает жесткую дополняемость факторов производства. Это означает, что факторы могут использоваться только в строго определенной пропорции, нарушение которой технологически невозможно. Например, авиационный рейс может быть нормально осуществлен при наличии как минимум одного самолета и пяти членов экипажа. При этом нельзя увеличивать самолето-часы (капитал), одновременно сокращая человеко-часы (труд), и наоборот, и сохранять неизменным выпуск. Изокванты в данном случае имеют вид прямых углов, т.е. предельные нормы технической замены равны нулю (рис. 8.6). В то же время можно увеличивать выпуск (количество рейсов), увеличивая в одной и той же пропорции и труд, и капитал. Графически это означает переход на более высокую изокванту.

Рис. 8.6. Изокванты в случае жесткой дополняемости факторов производства

Аналитически такая производственная функция имеет вид: q =min {aK; bL}, гдеа иb — постоянные коэффициенты, отражающие производительность соответственно капитала и труда. Соотношение этих коэффициентов определяет пропорцию использования капитала и труда.

В нашем примере с авиарейсом производственная функция выглядит так: q = min{1K; 0,2L}. Дело в том, что производительность капитала здесь составляет один рейс на один самолет, а производительность труда — один рейс на пять человек или 0,2 рейса на одного человека. Если авиакомпания располагает самолетным парком в 10 машин и имеет 40 человек летного персонала, то ее максимальный выпуск составит:q = min{ 1 х 8; 0,2 х 40} = 8 рейсов. Два самолета при этом будут простаивать на земле из-за нехватки персонала.

Рассмотрим случай, когда имеет место совершенная замещаемость факторов производства. Допустим, например, что на складских работах можно использовать квалифицированных и неквалифицированных грузчиков, причем производительность квалифицированного грузчика вN раз выше, чем неквалифицированного. Это означает, что мы можем заменить любое количество квалифицированных грузчиков неквалифицированными в соотношенииN к одному. И наоборот, можно заменить N неквалифицированных грузчиков одним квалифицированным.

Производственная функция при этом имеет вид: где — число квалифицированных рабочих, — число неквалифицированных рабочих,а и b — постоянные параметры, отражающие производительность соответственно одного квалифицированного и одного неквалифицированного рабочего.Соотношение коэффициентов а и b — предельная норма технической замены неквалифицированных грузчиков квалифицированными. Она постоянна и равнаN: MRTS_xy = a/b = N.

Пусть, например, квалифицированный грузчик в состоянии в единицу времени обработать 3 т груза (это будет коэффициент а в производственной функции), а неквалифицированный — только 1 т (коэффициент b). Значит, работодатель может отказаться от трех неквалифицированных грузчиков, дополнительно нанимая одного квалифицированного грузчика, чтобы выпуск (общий вес обработанного груза) при этом остался прежним.

Изокванта в данном случае является линейной (рис. 8.5).

Рис. 8.5. Изокванта при совершенной заменяемости факторов

Тангенс угла наклона изокванты равен предельной норме технической замены неквалифицированных грузчиков квалифицированными.

Взглянем, наконец, на производственную функцию, предполагающую существование ограниченного числа производственных технологийдля производства заданного количества продукции. Каждой из них соответствует определенное состояние труда и капитала. В результате мы имеем ряд опорных точек в пространстве «труд-капитал», соединив которые, получаем ломаную изокванту (рис. 8.7).

Рис. 8.7. Ломаные изокванты при наличии ограниченного числа производственных методов

На рисунке видно, что выпуск продукции в объемеq₁ можно получить при четырех комбинациях труда и капитала, соответствующих точкамА, B, С иD. Возможны также и промежуточные комбинации, достижимые в тех случаях, когда предприятие совместно использует две технологии для получения определенного совокупного выпуска. Как всегда, увеличив количества труда и капитала, мы переходим на более высокую изокванту.

Кривые безразличия

Кривые безразличия — представляют собой совокупность точек на координатной плоскости, каждая из которых является потребительским набором, обеспечивающим потребителю одинаковый уровень удовлетворения его потребностей (или если пользоваться терминологией кардиналистского направления, одинаковую полезность).

Форма кривой безразличия отдельного потребителя определяется исключительно его вкусами и предпочтениями и не зависит от доходов или цен на потребляемые товары. Совокупность кривых безразличия, описывающих поведение одного потребителя, составляет его карту безразличия.

Исходные аксиомы анализа

Построение и анализ этих кривых основывается на следующих допущениях, или аксиомах:

Аксиома рациональности потребителя как экономического субъекта

Аксиома непрерывности
Все товары можно непрерывно разбить на всё более мелкие единицы, так что размеры единиц, в которых продается товар, не сдерживают потребителей.

Аксиома возможности выбора
Предполагает способность человека однозначно ответить на вопрос, какой из предложенных потребительских наборов, А или В, является для него более предпочтительным. При этом обязательным будет выбор одного из трех вариантов ответа: либо набор А предпочтительней набора В (А > B), либо набор B предпочтительней набора A (A < B), либо наборы A и B имеют одинаковую полезность для потребителя (A=B).

Аксиома транзитивности
Согласно этой аксиоме для любых трех потребительских корзин (наборов) А, В и С, если потребитель предпочитает набор A в большей степени, чем набор B, и набор B в большей степени чем набор C, то он однозначно предпочитает потребительских набор A в большей степени, чем набор C. То есть если A > B и B > C значит A >C.
То же самое справедливо и для правила: если A = B и B = C, то A = C.

Аксиома ненасыщенности
Для любого набора A всегда существует набор B, более предпочтительный для потребителя. Это означает, что у потребителя нет порога насыщения и он всегда предпочитает иметь большее количество товаров меньшему. При этом, если количество хотя бы одного из товаров, входящих в потребительскую корзину возрастет, уровень его удовлетворения увеличится.