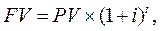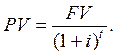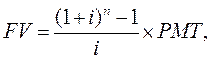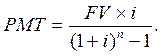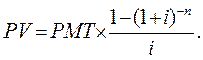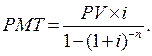Временна́я це́нность де́нег (ВЦД) или стоимость денег во времени (СДВ), стоимость денег с учётом фактора времени - теория временной стоимости денег, дисконтированная существующая ценность — концепция, на которой основано предположение о том, что деньги должны приносить процент — ценность сегодняшних денег выше, чем ценность той же суммы, получаемой в будущем.
Временна́я ценность денег — одно из фундаментальных понятий финансов, основанное на предпосылке, что каждый предпочтёт получить определенную сумму денег сегодня, чем то же самое количество в будущем, при прочих равных условиях. В результате, когда каждый вносит деньги на счёт в банк, каждый требует (и зарабатывает) проценты.
«Золотое» правило бизнеса гласит:
Сумма, полученная сегодня, больше той же суммы, полученной завтра. авт. (Леонардо Пизанский (Фибоначчи) 1202 г. н. э.)
Согласно принципу временно́й ценности денег, сегодняшние поступления ценнее будущих. Отсюда вытекает, по крайней мере, два важных следствия:
необходимость учёта фактора времени при проведении финансовых операций;
некорректность (с точки зрения анализа долгосрочных финансовых операций) суммирования денежных величин, относящихся к разным периодам времени.
В финансовом менеджменте для работы с денежными величинами в разных периодах времени выполняют приведение этих денежных величин к одному периоду. Для этого денежные величины или потоки денежных платежей пересчитывают по ставке дисконтирования на какой-то период:
дисконтированная стоимость (PV, present value) и дисконтированная стоимость аннуитета;
будущая стоимость денег (FV, future value)
Будущая стоимость денег рассчитывается на конец рассматриваемого периода, а текущая (дисконтированная) — соответственно на текущий момент. Как правило, приведенная стоимость денег рассчитывается по сложному проценту. В качестве ставки дисконтирования используется или планируемая доходность инвестиционного проекта, или минимальная ставка. Минимальная ставка обычно принимается за ставку рефинансирования, или процент по считающимся безрисквыми долгосрочным государственным облигациям, или процент по банковским депозитам.
Функции сложного процента
Сложный процент – модель расчета, при которой проценты прибавляются к основной сумме [вклада] и в дальнейшем сами участвуют в создании новых процентов.
Шесть функций сложного процента (подразумевается, что платежи возникают в конце соответствующего периода):
Таблица 1.
| № п/п | Наименование функции | Формула расчета, пример решения задачи | ||||||||||||||
| 1 | Накопленная (будущая) сумма единицы | Показывает накопление 1 ден.ед. за период:
| ||||||||||||||
| 2 | Текущая стоимость единицы | Показывает текущую стоимость 1 ден.ед., которая возникает в будущем:
| ||||||||||||||
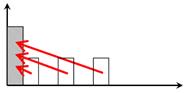
| 3 | Накопление единицы за период | Показывает, какой по истечении всего срока будет будущая стоимость серии аннуитетных платежей:
Аннуитетный – серия равновеликих периодических платежей. | ||||||||||||||
| 4 | Фактор фонда возмещения | Показывает величину единичного аннуитетного платежа, который необходим для того, чтобы к концу срока накопить 1 ден.ед.:
| ||||||||||||||
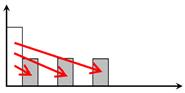
| 5 | Текущая стоимость обычного аннуитета | Показывает величину текущей стоимости будущего аннуитетных платежей:
| ||||||||||||||
| 6 | Взнос на амортизацию единицы | Показывает величину будущего аннуитетного платежа, необходимого для полной амортизации (погашения) кредита:
|
Зависимость между ставками накопления (дисконтирования) для различных по продолжительности периодов времени начисления:
базовый вариант
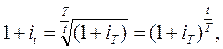
| упрощенный вариант
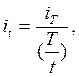
| ||||||
| |||||||
Таблица 2.