Количественная оценка информации этого уровня не связана с содержательной стороной информации, а оперирует с обезличенной информацией, не выражающей смыслового отношения к объекту. В связи с этим данная мера дает возможность оценки информационных потоков в таких разных по своей природе объектах, как системы связи, вычислительные машины, системы управления, нервная система живого организма и т. п.
Для измерения информации на синтаксическом уровне вводятся два параметра: объем информации (данных) – Vд (объемный подход) и количество информации – I(энтропийный подход).
Объем информацииVд (объемный подход). При реализации информационных процессов информация передается в виде сообщения, представляющего собой совокупность символов какого-либо алфавита. При этом каждый новый символ в сообщении увеличивает количество информации, представленной последовательностью символов данного алфавита. Если теперь количество информации, содержащейся в сообщении из одного символа, принять за единицу, то объем информации (данных) Vд в любом другом сообщении будет равен количеству символов (разрядов) в этом сообщении. Так как одна и та же информация может быть представлена многими разными способами (с использованием разных алфавитов), то и единица измерения информации (данных) соответственно будет меняться.
Так, в десятичной системе счисления один разряд имеет вес, равный 10, и соответственно единицей измерения информации будет дит (десятичный разряд). В этом случае сообщение в виде п-разрядного числа имеет объем данных Vд = п дит. Например, четырехразрядное число 2009 имеет объем данных Vд = 4 дит.
В двоичной системе счисления один разряд имеет вес, равный 2, и соответственно единицей измерения информации будет бит (bit (binary digit) – двоичный разряд). В этом случае сообщение в виде n-разрядного числа имеет объем данных Vд = п бит. Например, восьмиразрядный двоичный код 11001011 имеет объем данных Vд = 8 бит.
В современной вычислительной технике наряду с минимальной единицей измерения данных бит широко используется укрупненная единица измерения байт, равная 8 бит. Именно восемь битов требуется для того, чтобы закодировать любой из 256 символов алфавита клавиатуры компьютера (256=28).
При работе с большими объемами информации для подсчета ее количества применяют более крупные единицы измерения:
1 Килобайт (Кбайт) = 1024 байт = 210 байт,
1 Мегабайт (Мбайт) = 1024 Кбайт = 220 байт = 1 048 576 байт;
1 Гигабайт (Гбайт) = 1024 Мбайт = 230 байт = 1 073 741 824 байт;
В последнее время в связи с увеличением объёмов обрабатываемой информации входят в употребление такие производные единицы, как:
1 Терабайт (Тбайт) = 1024 Гбайт = 240 байт = 1 099 511 627 776 байт;
1 Петабайт (Пбайт) = 1024 Тбайт = 250 байт = 1 125 899 906 842 624 байт.
Следует обратить внимание, что в системе измерения двоичной (компьютерной) информации, в отличие от метрической системы, единицы с приставками «кило», «мега» и т. д. получаются путем умножения основной единицы не на 103 = 1000, 106 = 1 000 000 и т. д., а на 210 = 1024, 220 = 1 048 576 и т. д.
Количество информации I (энтропийный подход). В теории информации и кодирования принят энтропийный подход к измерению информации. Этот подход основан на том, что факт получения информации всегда связан с уменьшением разнообразия или неопределенности (энтропии) системы. Исходя из этого, количество информации в сообщении определяется как мера уменьшения неопределенности состояния данной системы после получения сообщения. Неопределенность может быть интерпретирована в смысле того, насколько мало известно наблюдателю о данной системе. Как только наблюдатель выявил что-нибудь в физической системе, энтропия системы снизилась, так как для наблюдателя система стала более упорядоченной.
Таким образом, при энтропийном подходе под информацией понимается количественная величина исчезнувшей в ходе какого-либо процесса (испытания, измерения и т.д.) неопределенности. При этом в качестве меры неопределенности вводится энтропия Н, а количество информации равно:
I = Hapr – Haps
где, Hapr – априорная энтропия о состоянии исследуемой системы или процесса;
Haps – апостериорная энтропия.
Апостериори (от лат. a posteriori – из последующего) – происходящее из опыта (испытания, измерения).
Априори (от лат. a priori – из предшествующего) – понятие, характеризующее знание, предшествующее опыту (испытанию), и независимое от него.
В случае, когда в ходе испытания имевшаяся неопределенность снята (получен конкретный результат, т. е. Н = 0), количество полученной информации совпадает с первоначальной энтропией
I = Hapr
Рассмотрим в качестве исследуемой системы дискретный источник информации (источник дискретных сообщений), под которым будем понимать физическую систему, имеющую конечное множество возможных состояний {аi}, i = 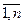 .
.
Все множество А = {a1, a2, ..., аn} состояний системы в теории информации называют абстрактным алфавитом или алфавитом источника сообщений.
Отдельные состояния a1, а2,..., аn называют буквами или символами алфавита.
Такая система может в каждый момент времени случайным образом принять одно из конечных множеств возможных состояний ai. При этом говорят, что различные состояния реализуются вследствие выбора их источником.
Получатель информации (сообщения) имеет определенное представление о возможных наступлениях некоторых событий. Эти представления в общем случае недостоверны и выражаются вероятностями, с которыми он ожидает то или иное событие. Общая мера неопределенности (энтропия) характеризуется некоторой математической зависимостью от этих вероятностей, количество информации в сообщении определяется тем, насколько уменьшается мера неопределенности после получения сообщения.
Поясним эту идею на примере.
Пусть у нас имеется 32 различные карты. Возможность выбора одной карты из колоды – 32. До произведения выбора, естественно предложить, что шансы выбрать некоторую определенную карту, одинаковы для всех карт. Произведя выбор, мы устраняем эту неопределенность. При этом неопределенность можно охарактеризовать количеством возможных равновероятностных выборов. Если теперь определить количество информации как меру устранения неопределенности, то полученную в результате выбора информацию можно охарактеризовать числом 32. Однако удобнее использовать не само это число, а логарифм от полученной выше оценки по основанию 2:
H = log2 m,
где m – число возможных равновероятных выборов (При m=2, получим информацию в один бит). То есть в нашем случае
H = log2 32 = 5.
Изложенный подход принадлежит английскому математику Р. Хартли (1928 г.). Он имеет любопытную интерпретацию. Он характеризуется числом вопросов с ответами «да» или «нет», позволяющим определить, какую карту выбрал человек. Таких вопросов достаточно 5.
Если при выборе карты, возможность появления каждой карты не одинаковы (разновероятны), то получим статистический подход к измерению информации, предложенный К. Шенноном (1948 г.). В этом случае мера информации измеряется по формуле:
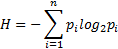
где pi – вероятность выбора i-го символа алфавита.
Легко заметить, что если вероятности p1, ..., pn равны, то каждая из них равна 1/N, и формула Шеннона превращается в формулу Хартли.
Меры информации семантического уровня. Для измерения смыслового содержания информации, т. е. ее количества на семантическом уровне, наибольшее распространение получила тезаурусная мера, которая связывает семантические свойства информации со способностью пользователя принимать поступившее сообщение. Действительно, для понимания и использования полученной информации получатель должен обладать определенным запасом знаний. Полное незнание предмета не позволяет извлечь полезную информацию из принятого сообщения об этом предмете. По мере роста знаний о предмете растет и количество полезной информации, извлекаемой из сообщения.
Если назвать имеющиеся у получателя знания о данном предмете тезаурусом (т. е. неким сводом слов, понятий, названий объектов, связанных смысловыми связями), то количество информации, содержащееся в некотором сообщении, можно оценить степенью изменения индивидуального тезауруса под воздействием данного сообщения.
Тезаурус — совокупность сведений, которыми располагает пользователь или система.
Иными словами, количество семантической информации, извлекаемой получателем из поступающих сообщений, зависит от степени подготовленности его тезауруса для восприятия такой информации.
В зависимости от соотношений между смысловым содержанием информации S и тезаурусом пользователя Sp изменяется количество семантической информации Iс, воспринимаемой пользователем и включаемой им в дальнейшем в свой тезаурус. Характер такой зависимости показан на рис. 2.1. Рассмотрим два предельных случая, когда количество семантической информации Iс равно 0:
а) при Sp = 0 пользователь не воспринимает (не понимает) поступающую информацию;
б) при S —> ∞ пользователь «все знает», и поступающая информация ему не нужна.
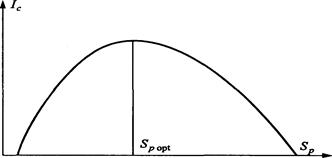
Рис. 1.2. Зависимость количества семантической информации,
воспринимаемой потребителем, от его тезауруса Ic=f(Sp)
Максимальное количество семантической информации потребитель приобретает при согласовании ее смыслового содержания S со своим тезаурусом Sp (S = Sp opt), когда поступающая информация понятна пользователю и несет ему ранее неизвестные (отсутствующие в его тезаурусе) сведения.
Следовательно, количество семантической информации в сообщении, количество новых знаний, получаемых пользователем, является величиной относительной. Одно и то же сообщение может иметь смысловое содержание для компетентного пользователя и быть бессмысленным для пользователя некомпетентного.
При оценке семантического (содержательного) аспекта информации необходимо стремиться к согласованию величин S и Sp.
Относительной мерой количества семантической информации может служить коэффициент содержательности С, который определяется как отношение количества семантической информации к ее объему:
С = Iс / Vд
Меры информации прагматического уровня. Эта мера определяет полезность информации для достижения пользователем поставленной цели. Эта мера также величина относительная, обусловленная особенностями использования этой информации в той или иной системе.
Одним из первых российских ученых к проблеме оценки информации прагматического уровня обратился А.А. Харкевич, который предложил принять за меру ценности информации количество информации, необходимое для достижения поставленной цели, т. е. рассчитывать приращение вероятности достижения цели. Так, если до получения информации вероятность достижения цели равнялась р0, а после ее получения – p1 то ценность информации определяется как логарифм отношения p1/p0:
I = log2 p1 – log2 р0 = log2 (p1/p0)
Таким образом, ценность информации при этом измеряется в единицах информации, в данном случае в битах.
Кодирование текстовой информации
Вспомним некоторые известные нам факты: Множество символов, с помощью которых записывается текст, называется алфавитом. Число символов в алфавите – это его мощность. Формула определения количества информации: N = 2b, где N – мощность алфавита (количество символов), b – количество бит (информационный вес символа). В алфавит мощностью 256 символов можно поместить практически все необходимые символы. Такой алфавит называется достаточным. Т.к. 256 = 28, то вес 1 символа – 8 бит. Единице измерения 8 бит присвоили название 1 байт: 1 байт = 8 бит. Двоичный код каждого символа в компьютерном тексте занимает 1 байт памяти. |
Дата: 2019-11-01, просмотров: 267.
