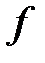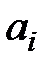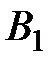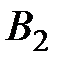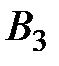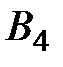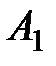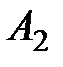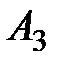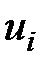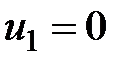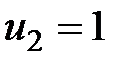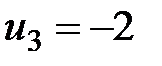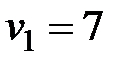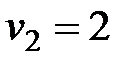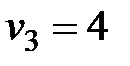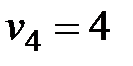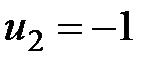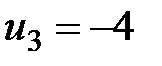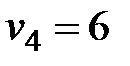Рассмотрим работу алгоритма на примере компании Mikks. Приведем еще раз ее математическую модель:
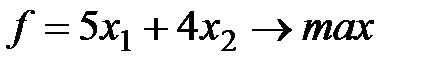
при выполнении следующих ограничений:
, 
.
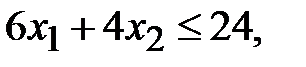
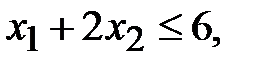
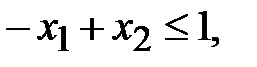
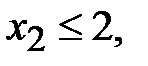
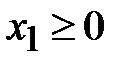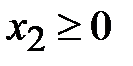Эта задача в стандартной форме записывается так:
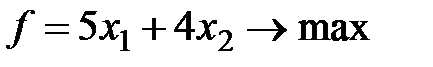
при выполнении следующих ограничений:
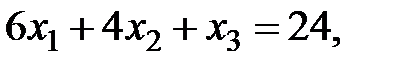
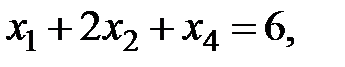
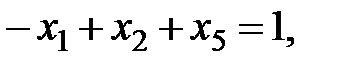
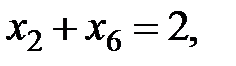
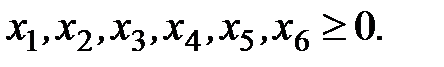
Здесь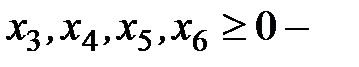 
дополнительные (остаточные) переменные, добавленные в неравенства для преобразования их в равенства.
Ручные вычисления по симплекс-методу удобно оформлять в виде так называемых симплекс-таблиц (СТ).
| Базисные переменные |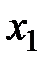 
| 
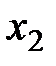
| Свободные члены |
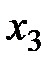
| 6 | 4 | 24 |
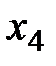
| 1 | 2 | 6 |
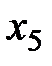
| -1 | 1 | 1 |
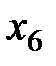
| 0 | 1 | 2 |
|
| -5 | -4 | 0 |
Замечание. Если целевую функцию необходимо максимизировать, то предварительно нужно умножить ее на (–1).
Сформулируем алгоритм СМ применительно к данным, внесенным в таблице.
Шаг 1. Выяснить, имеются ли в последней строке таблицы отрицательные числа (значение в последнем столбце не принимается во внимание). Если все числа неотрицательны, то процесс закончен; базисное решение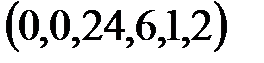 
является оптимальным; 
.
Если в последней строке имеются отрицательные числа, перейти к Шагу 2.
Шаг 2.
Просмотреть столбец, соответствующий наименьшему отрицательному числу и выяснить, имеются ли в нем положительные числа. Если ни в одном из таких столбцов нет положительных чисел, то оптимального решения не существует.
Если найден столбец, содержащий хотя бы один положительный элемент, отметить его и перейти к Шагу 3.
Шаг 3. Разделить свободные члены на соответствующие положительные числа из выделенного столбца и выбрать наименьшее частное. Отметить строку, соответствующую наименьшему частному (горизонтальной стрелкой). Выделить разрешающий элемент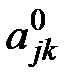 
, стоящий на пересечении отмеченных строки и столбца. Перейти к Шагу 4.
Шаг 4.
1. Поменять местами переменные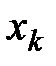 
и 
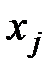, остальные переменные оставить на прежних местах.
2. На место опорного элемента поставить число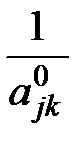 
.
3. На остальных местах разрешающей (опорной) строки записать соответствующие элементы исходной таблицы, делённые на опорный элемент.
4. На свободные места разрешающего столбца поставить со знаком минус соответствующие элементы исходной таблицы, делённые на опорный элемент.
Шаг 5.
Оставшиеся свободные места в новой СТ заполнить построчно следующим образом: из строки элементов исходной таблицы вычесть произведение ее элемента из разрешающего столбца на уже заполненную разрешающую строку новой таблицы.
На этом заполнение новой таблицы заканчивается и происходит переход к Шагу 1.
Пример 2.5. Приведем ход решения задачи по данному алгоритму:
| Базисные переменные |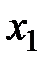
|
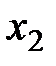
| Свободные члены |
|
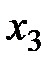
| 6 | 4 | 24 |
|
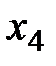
| 1 | 2 | 6 |
|
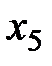
| -1 | 1 | 1 |
|
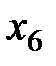
| 0 | 1 | 2 |
|
| -5 | -4 | 0 |
| Базисные переменные |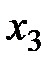
|
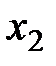
| Свободные члены |
|
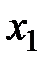
| 0,17 | 0,67 | 4,00 |
|
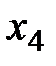
| -0,17 | 1,33 | 2,00 |
|
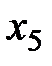
| 0,17 | 1,67 | 5,00 |
|
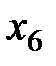
| 0,00 | 1,00 | 2,00 |
|
| 0,83 | -0,67 | 20,00 |
| Базисные переменные |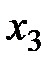
|
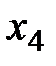
| Свободные члены |
|
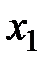
| 0,25 | -0,50 | 3,00 |
|
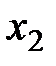
| -0,13 | 0,75 | 1,50 |
|
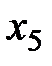
| 0,38 | -1,25 | 2,50 |
|
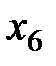
| 0,13 | -0,75 | 0,50 |
|
| 0,75 | 0,50 | 21,00 |
Ответ: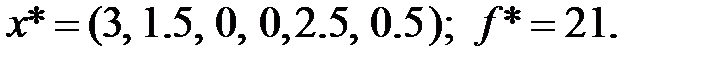 
Транспортная задача
Транспортная задача является особым типом задач целочисленного программирования, для которых разработаны простые и эффективные способы нахождения оптимального решения, не требующие громоздких вычислений. Экономико-математическую модель транспортной задачи рассмотрим на следующем примере.
Пример 2.6. Имеются три поставщика некоторого товара и четыре потребителя этого товара. Причём известна стоимость перевозки товара от каждого поставщика к каждому потребителю. Требуется найти объёмы перевозок для каждой пары "поставщик − потребитель" так, чтобы суммарные затраты на перевозку были минимальны, запасы всех поставщиков реализованы и потребности всех потребителей удовлетворены (табл.2.1).
Таблица 2.1.
| Поставщики | Потребители | Запасы поставщиков, | |||||||
|
|
|
|
| ||||||
|
| 7 | 2 | 4 | 8 | 340 | ||||
| 
| 
| 
| ||||||
|
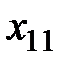
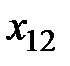
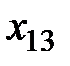
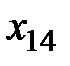
| 8 | 9 | 6 | 5 | 200 | ||||
| 
| 
| 
| ||||||
|
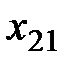
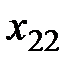
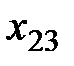
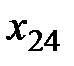
| 3 | 5 | 7 | 2 | 160 | ||||
| 
| 
| 
| ||||||
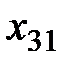
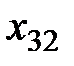
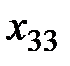
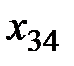
Спрос потребителей,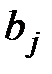 
| 120 | 170 | 150 | 260 |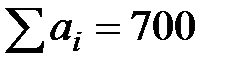 
| ||||
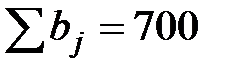
В левом верхнем углу произвольной клетки стоит коэффициент, равный стоимости перевозки от поставщика, номер которого указан в этой строке, к потребителю, номер которого указан в столбце.
В теории транспортной задачи таблица вида табл. 2.1 называется таблицей поставок.
Построим экономико-математическую модель данной задачи, обозначив через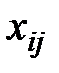 
объем поставляемого товара от i -го поставщика к j- му потребителю. Чтобы запасы каждого поставщика были полностью реализованы, должны быть справедливы уравнения баланса для каждой строки таблицы поставок, т. е. выполняться равенства
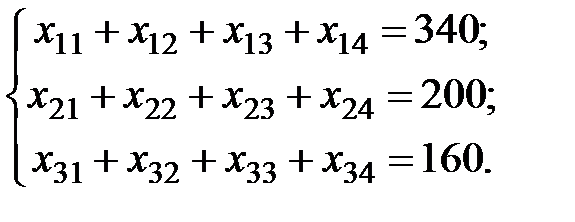(2.4)
Чтобы спрос каждого из потребителей был удовлетворён, должны быть справедливы уравнения баланса для каждого столбца таблицы поставок, то есть
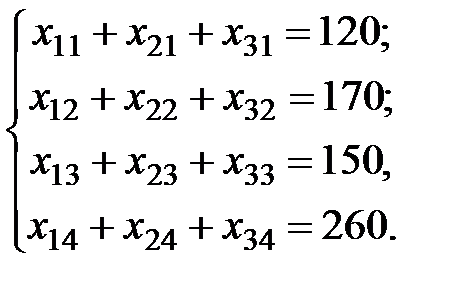(2.5)
Поскольку объём перевозимого груза величина неотрицательная, то должны выполняться ограничения на переменные :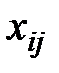
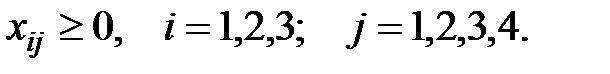
Суммарные затраты F на перевозку определяются указанными в таблице поставок тарифами перевозок и размерами поставок:
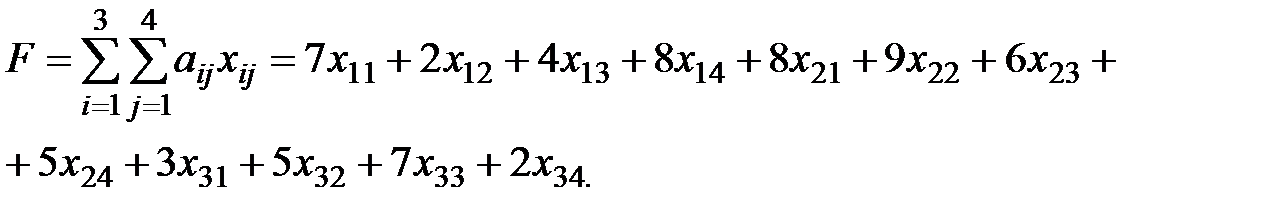(2.6)
Решить транспортную задачу − значит на множестве неотрицательных решений системы ограничений найти такое решение, при котором линейная функция принимает минимальное значение.
Транспортная задача называется закрытой (сбалансированной) , если сумма запасов всех n поставщиков равна сумме потребностей всех m потребителей:
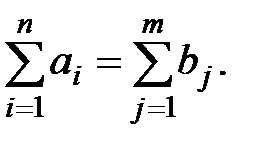
В противном случае транспортная задача называется открытой. Решение открытой транспортной задачи сводят к решению закрытой транспортной задачи введением фиктивных потребителей, когда сумма запасов превышает сумму потребностей, или фиктивных поставщиков, когда сумма потребностей превышает сумму запасов. При этом тарифы перевозок для фиктивных поставщиков и потребителей принимаются равными нулю.
Число основных (базисных) переменных закрытой транспортной задачи равно m + n −1, где n − число поставщиков; m − число потребителей; так как в закрытой транспортной задаче сумма запасов всех поставщиков равна сумме потребностей всех потребителей.
При заполнении таблицы поставок клетки, соответствующие неосновным (свободным) переменным, оставляют пустыми, а в клетки, соответствующие базисным переменным, проставляют числа, определяющие количество поставки . В частности, если транспортная задача вырожденная, некоторые поставки могут иметь нулевую величину и в этом случае в базисную клетку записываем число 0.
Нахождение первоначального базисного распределения – опорного плана задачи − возможно любым из известных методов: наименьшей стоимости, "северо-западного угла", Фогеля, наибольшего предпочтения.
Рассмотрим метод "северо-западного угла". "Северо-западным углом" называется ячейка таблицы поставок, соответствующая значению переменной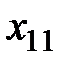 
. В эту ячейку записываем максимально возможную поставку, определяя её по формуле
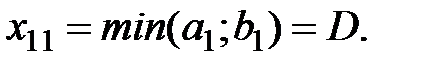(2.7)
Если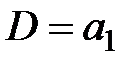 
, то запас первого поставщика распределен полностью, и переходим к заполнению клетки с 
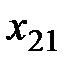, записывая в неё наименьшее из чисел 
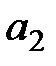и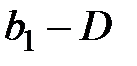 
. Если 
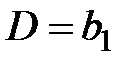, то полностью удовлетворена потребность первого потребителя, тогда переходим к заполнению клетки с 
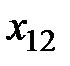, записывая в неё наименьшее из чисел 
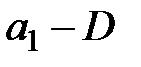и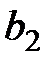 
. Так, постепенно двигаясь по таблице поставок, распределяем все запасы и удовлетворяем все потребности. Движение по таблице поставок может быть или по горизонтали, или строго по вертикали, а повороты при движении по трассе делаются только под прямым углом.
При заполнении таблицы следим за выполнением баланса по строкам и столбцам. Число заполненных клеток в полученном распределении должно быть равным числу базисных (основных) переменных. Если поворот происходит в клетке, где размер поставки равен нулю, то говорят о вырожденном плане поставок. В этом случае нулевая поставка записывается в клетку, где трасса распределения поставок делает поворот, и клетка считается занятой.
Если распределение выполняется без вычислительных ошибок, в последнюю заполняемую клетку запишется число, получаемое автоматически и равное остатку нераспределённых количеств у последнего из участвующих в распределении поставщиков или количеству неудовлетворённого спроса последнего потребителя.
Получаемое распределение по методу "северо-западного угла" для транспортной задачи, исходные данные которой содержатся в табл. 2.1, показано в табл. 2.2.
Найденный опорный план записывается матрицей
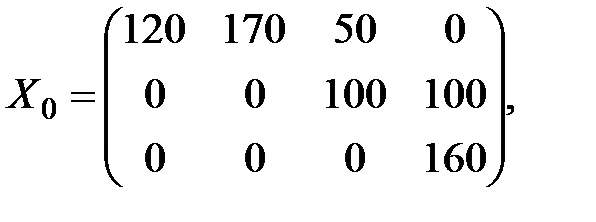
а значение целевой функции на этом плане, равное стоимости поставок, равно
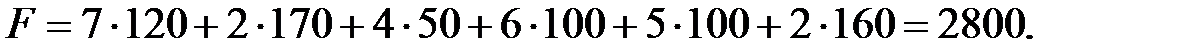
Таблица 2.2.
| Поставщики | Потребители | Запасы поставщиков, | |||||||
|
|
|
|
| ||||||
|
| 7 | 2 | 4 | 8 | 340 | ||||
| 120 | 170 | 50 | |||||||
|
| 8 | 9 | 6 | 5 | 200 | ||||
| 100 | 100 | ||||||||
|
| 3 | 5 | 7 | 2 | 160 | ||||
| 160 | |||||||||
| Спрос потребителей,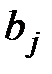
| 120 | 170 | 150 | 260 |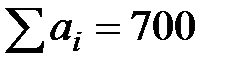
| ||||
Другим методом определения опорного плана поставок является метод наименьшей стоимости.
В первую очередь при определении объёмов поставок занимают клетки, имеющие наименьшие тарифы перевозок. Так, в рассматриваемом примере начнём с клетки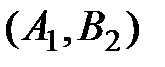 
, имеющей тариф 2. От первого поставщика ко второму потребителю поставим максимально возможное количество груза, а именно 
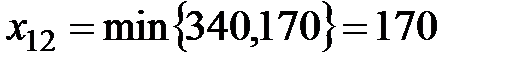. Потребности второго потребителя полностью удовлетворены, и все клетки второго столбца далее не рассматриваем.
На втором шаге распределения выбираем клетку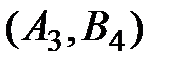 
с тарифом 2 и делаем в неё поставку 
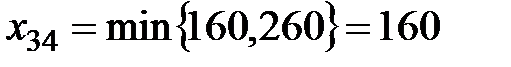. Теперь запас третьего поставщика полностью израсходован и все клетки третьей строки далее не рассматриваем.
Соответственно, по наименьшим значениям остающихся неиспользованными в табл. 2.3 тарифов делаем следующие поставки:
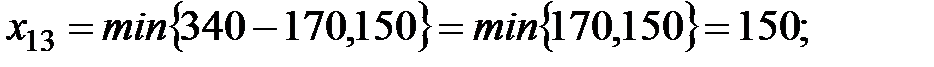
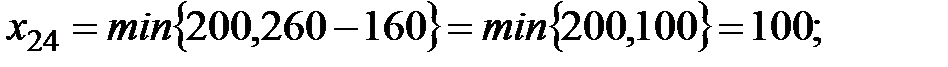
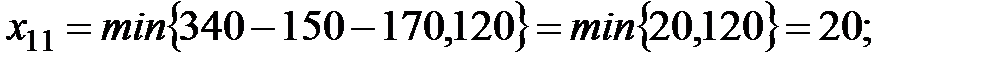
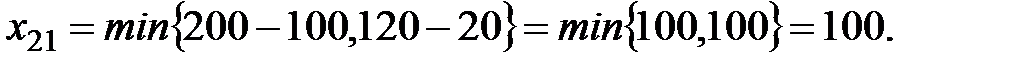
Последняя поставка получается автоматически, так как остаётся только одна клетка для заполнения и туда помещается остаток запасов и потребностей. Они равны, поскольку сумма всех запасов и сумма всех потребностей равны.
Таблица 2.3.
| Поставщики | Потребители | Запасы поставщиков, | |||||||
|
|
|
|
| ||||||
|
| 7 | 2 | 4 | 8 | 340 | ||||
| 20 | 170 | 150 | |||||||
|
| 8 | 9 | 6 | 5 | 200 | ||||
| 100 | 100 | ||||||||
|
| 3 | 5 | 7 | 2 | 160 | ||||
| 160 | |||||||||
| Спрос потребителей,
| 120 | 170 | 150 | 260 |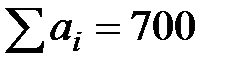
| ||||
Найденный опорный план записывается матрицей
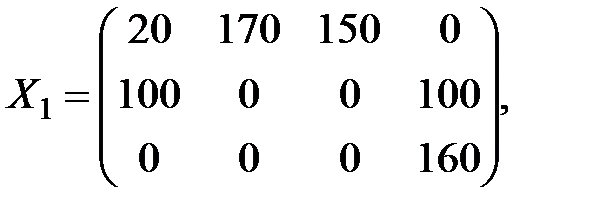
а значение целевой функции на этом плане равно
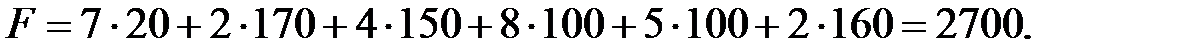
Методом наименьшей стоимости получился лучший опорный план, так как значение целевой функции на нем меньше на 100 единиц. Тем не менее, и этот план может быть не оптимальным.
Критерий оптимальности для транспортной задачи: базисное распределение поставок оптимально тогда и только тогда, когда оценки всех свободных клеток неотрицательны.
Для определения оценок свободных клеток используют два взаимозаменяемых метода: распределительный и потенциалов. Рассмотрим один из них, а именно метод потенциалов.
Потенциалы - числа для нахождения оценок допустимого плана, полученного в ходе распределения запасов поставщиков. Потенциалы для поставщиков и потребителей вычисляются по тарифам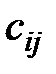 
занятых клеток таблицы поставок. Для потенциалов поставщиков 
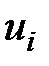и потребителей 
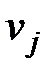, соответствующих занятым клеткам, справедливы равенства
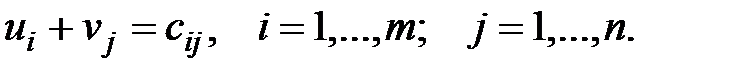(2.8)
Так как занятых клеток на одну меньше, чем число потенциалов, значение одного из потенциалов (все равно какого) назначается произвольно и может быть любым действительным числом (обычно полагают равным нулю, чтобы не усложнять вычисления остальных потенциалов).
Разрешая равенства (2.8) относительно потенциалов, получаем их числовые значения. Оценки свободных клеток таблицы поставок рассчитываются по формулам
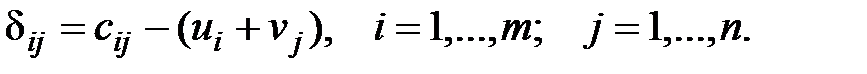(2.9)
Если построенное первоначальное решение не удовлетворяет критерию оптимальности, то среди свободных клеток, имеющих отрицательную оценку, выбираем ту, для которой абсолютная величина оценки наибольшая. Отмечаем эту клетку знаком " + " и строим из неё цикл.
Циклом в таблице поставок называют ломаную линию, проходящую через занятые клетки, начинающуюся и заканчивающуюся в одной и той же свободной клетке. Эта ломаная линия имеет вершины в клетках и звенья, лежащие вдоль строк и столбцов таблицы поставок. Причём ломаная должна быть связной, и в каждой вершине ломаной встречаются два звена, одно из которых располагается по строке, а другое − по столбцу. Клетки, через которые проходит ломаная линия, не делая в них поворота, называются транзитными, и имеющиеся в них поставки не участвуют в процессе перераспределения. Таким образом, цикл проходит через занятые клетки и только через одну свободную клетку, начинаясь и заканчиваясь в ней.
Последовательно отмечаем вершины цикла знаками " + " и " − " так, чтобы соседние вершины были отмечены противоположными знаками.
Среди поставок, находящихся в клетках помеченных знаком "−", выбираем наименьшую и помещаем ее в пустую клетку, помеченную знаком " + ". Затем рассчитываем новые значения поставок, прибавляя выбранное число ко всем поставкам, стоящим в клетках, помеченных знаком " + ", и вычитая его из всех поставок, стоящих в клетках, помеченных знаком " − ". Для вновь полученного плана поставок рассчитываем по занятым клеткам потенциалы, а затем оценки новых свободных клеток.
Если критерий оптимальности выполняется для полученного плана, то задача решена. В противном случае продолжаем процесс перераспределения поставок до тех пор, пока не будет получено оптимальное решение транспортной задачи.
Для вычисления оценки свободной клетки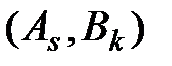 
таблицы поставок распределительным методом необходимо построить цикл для неё и найти оценку по формуле
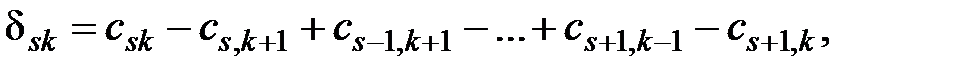
где записаны в порядке прохождения цикла с чередованием знаков "+" и "-" тарифы перевозок для всех клеток, образующих цикл оцениваемой свободной клетки.
Пример 2.7. Решить транспортную задачу с опорным планом, заданным в табл. 2.3, методом потенциалов.
Вычислим потенциалы для занятых клеток и результаты расчётов поместим в табл. 2.4:
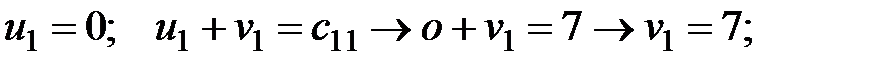
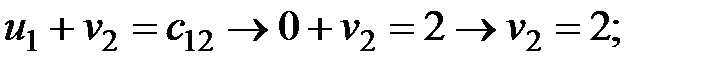
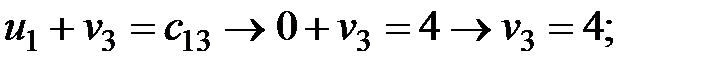
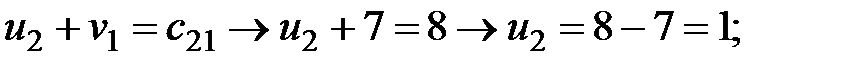
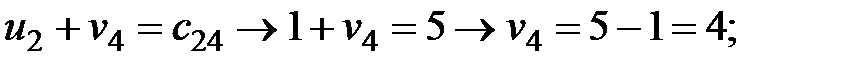
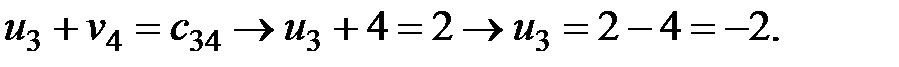
Рассчитаем оценки свободных клеток таблицы поставок:
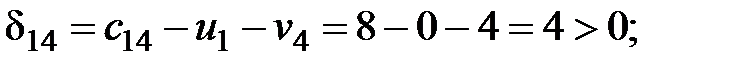
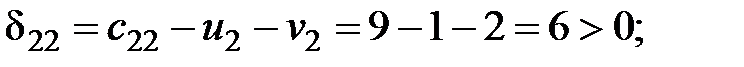
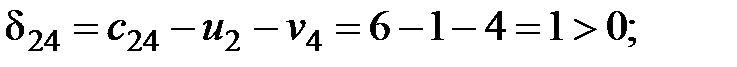
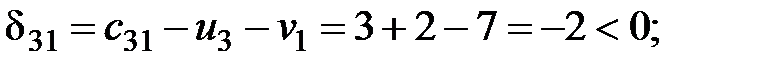
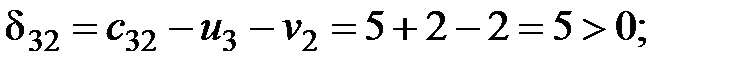
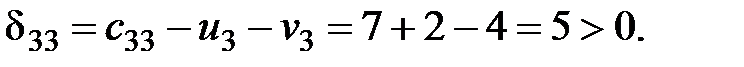
Таблица 2.4.
| Поставщики | Потребители | Запасы поставщиков, | Потенциалы | |||||||||
|
|
|
|
| |||||||||
|
| 7 | 2 | 4 | 8 | 340 |
| ||||||
| 170 | 150 | ||||||||||
|
| 8 | 9 | 6 | 5 |
| 200 |
| |||||
|
| 100 | |||||||||||
|
| 3 | 5 | 7 | 2 | 160 |
| ||||||
| 160 | ||||||||||||
| Спрос потребителей,
| 120 | 170 | 150 | 260 |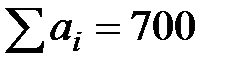
| |||||||
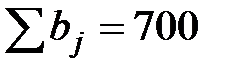
Потенциалы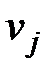 
|
|
|
|
| ||||||||
Среди найденных оценок одна меньше нуля, следовательно, найденный план не является оптимальным. Делаем перераспределение поставки в клетку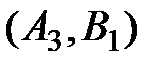 
. Цикл, найденный для перемены плана поставок, показан в табл. 2.4.
Находим размер перемещаемой в клетку 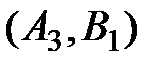поставки по размерам отмеченных знаком "-" поставок, а именно:
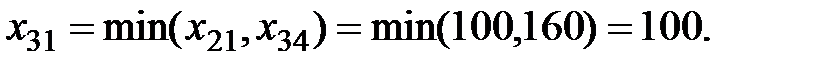
Прибавляем число 100 к поставкам, отмеченным знаком "+", вычитаем число 100 из поставок, отмеченных знаком "−", новое получаем распределение поставок. Заносим результаты в новую таблицу поставок (табл. 2.5). Для вновь полученного плана поставок и по тарифам занятых клеток считаем значения потенциалов.
Таблица 2.5.
| Поставщики | Потребители | Запасы поставщиков, | Потенциалы | |||||||
|
|
|
|
| |||||||
|
| 7 | 2 | 4 | 8 | 340 |
| ||||
| 20 | 170 | 150 | ||||||||
|
| 8 | 9 | 6 | 5 | 200 |
| ||||
| 200 | ||||||||||
|
| 3 | 5 | 7 | 2 | 160 |
| ||||
| 100 | 60 | |||||||||
| Спрос потребителей,
| 120 | 170 | 150 | 260 |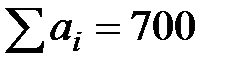
| |||||
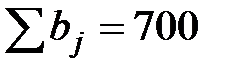
| Потенциалы
|
|
|
|
| ||||||
Находим оценки свободных клеток:
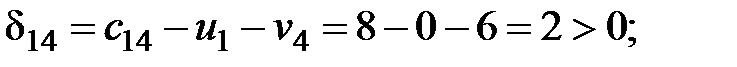
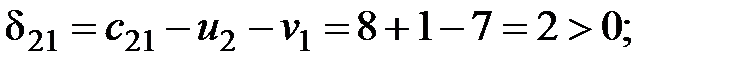
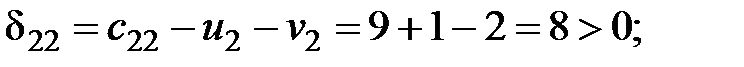
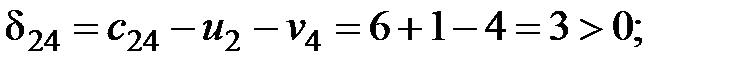
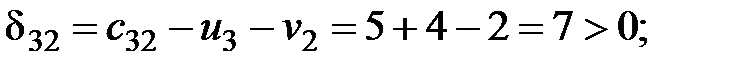
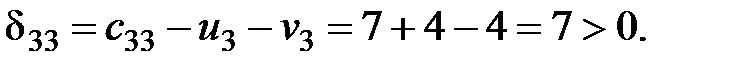
Для найденного плана
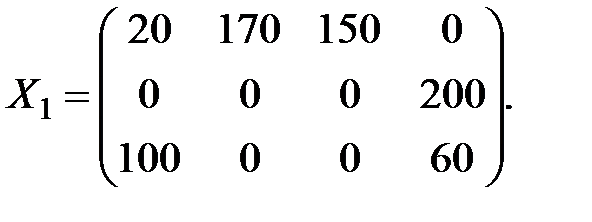
Подсчитаем значение целевой функции:
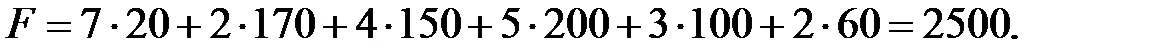
Поскольку все оценки свободных клеток положительные, найденный план является оптимальным планом транспортной задачи. Минимальная стоимость перевозок определяется значением целевой функции на этом плане, и она равна 2500 денежных единиц.
Дата: 2019-11-01, просмотров: 267.
