Рассмотренная методика Шеннона - Фано не всегда приводит к однозначному построению кода, т.к. при разбиении на подгруппы можно сделать большей по вероятности как верхнюю, так и нижнюю подгруппы:
Таблица 3.6.
| Знаки (буквы) xi | Вероятность Pi | 1-е кодовые комбинации | 2-е кодовые комбинации | ||||||||
| номер разбиения | номер разбиения | ||||||||||
| 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | ||
| x1 | 0,22 | 1 | 1 | 1 | 1 | ||||||
| x2 | 0,20 | 1 | 0 | 1 | 1 | 0 | |||||
| x3 | 0,16 | 1 | 0 | 0 | 0 | 1 | 1 | ||||
| x4 | 0,16 | 0 | 1 | 0 | 1 | 0 | |||||
| x5 | 0,10 | 0 | 0 | 1 | 0 | 0 | 1 | ||||
| x6 | 0,10 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | ||
| x7 | 0,04 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| x8 | 0,02 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
От указанного недостатка свободен метод Хаффмона.
Эта методика гарантирует однозначное построение кода с наименьшим для данного распределения вероятностей средним числом символов на букву.
Для двоичного кода метод Хаффмона сводится к следующему. Буквы алфавита сообщений выписывают в основной столбец таблицы в порядке убывания вероятностей. Две последние буквы объединяют в одну вспомогательную букву, которой приписывают суммарную вероятность. Вероятности букв, не участвующих в объединении и полученная суммарная вероятность снова располагаются в порядке убывания вероятностей в дополнительном столбце, а две последние объединяются.
Процесс продолжается до тех пор, пока не получат единственную вспомогательную букву с вероятностью, равной единице.
Используя метод Хаффмона, осуществим эффективное кодирование ансамбля из восьми знаков:
Таблица 3.7.
| Знаки | Вероятности | Вспомогательные столбцы | Новая комбинация | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |||
| x1 | 0,22 | 0,22 | 0,22 | 0,26 | 0,32 | 0,42 | 0,58 | 1 | 01 |
| x2 | 0,20 | 0,20 | 0,20 | 0,22 | 0,26 | 0,32 | 0,42 | 00 | |
| x3 | 0,16 | 0,16 | 0,16 | 0,20 | 0,22 | 0,26 | 111 | ||
| x4 | 0,16 | 0,16 | 0,16 | 0,16 | 0,20 | 110 | |||
| x5 | 0,10 | 0,10 | 0,10 | 0,16 | 100 | ||||
| x6 | 0,10 | 0,10 | 1011 | ||||||
| x7 | 0,04 | 0,06 | 10101 | ||||||
| x8 | 0,02 | 10100 | |||||||
Для наглядности построим кодовое дерево. Из точки, соответствующей вероятности 1, направляем две ветви, причем ветви с большей вероятностью присваиваем символ 1, а с меньшей 0.
Такое последовательное ветвление продолжаем до тех пор, пока не дойдем до вероятности каждой буквы.
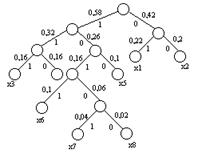
Рис. 3.1.
Двигаясь по кодовому дереву сверху вниз, можно записать для каждой буквы соответствующую ей кодовую комбинацию.
Пример21: Используя метод Шеннона - Фано и метод Хаффмона осуществить эффективное кодирование алфавита русского языка, характеризующегося ансамблем, представленным в примере 4.
4. Кодирование информации для канала с помехами
Ошибка в кодовой комбинации появляется при ее передаче по каналу связи вследствие замены одних элементов другими под воздействием помех. Например, 2-кратная ошибка возникает при замене (искажении) двух элементов. Например, если кодовая комбинация 0110111 принята как 0100110, то имеет место двукратная ошибка.
Теория помехоустойчивого кодирования базируется на результатах исследований, проведенных Шенноном и сформулированных в виде теоремы:
1. При любой производительности источника сообщений, меньшей, чем пропускная способность канала, существует такой способ кодирования, который позволяет обеспечить передачу всей информации, создаваемой источником сообщений, со сколь угодно малой вероятностью ошибки.
2. Не существует способа кодирования, позволяющего вести передачу информации со сколь угодно малой вероятностью ошибки, если производительность источника сообщений больше пропускной способности канала.
Из теоремы следует, что помехи в канале не накладывают ограничений на точность передачи. Ограничение накладывается только на скорость передачи, при которой может быть достигнута сколь угодно высокая точность передачи.
Теорема не затрагивает вопроса о путях построения кодов, обеспечивающих идеальную передачу информации, но, обосновав принципиальную возможность такого кодирования, позволяет вести разработку конкретных кодов.
При любой конечной скорости передачи информации вплоть до пропускной способности канала, сколь угодно малая вероятность ошибки достигается лишь при безграничном увеличении длительности кодируемых последовательностей знаков. Таким образом, безошибочная передача при наличии помех возможна лишь теоретически.
Обеспечение передачи информации с весьма малой вероятностью ошибки и достаточно высокой эффективностью возможно при кодировании чрезвычайно длинными последовательностями знаков.
На практике точность передачи информации и эффективность каналов связи ограничивается двумя факторами:
1) размером и стоимостью аппаратуры кодирования/декодирования;
2) временем задержки передаваемого сообщения.
Дата: 2019-07-30, просмотров: 375.