Рассмотрим ускорение Кориолиса, определяемое равенством (3.7). Если подвижная система движется относительно неподвижной поступательно (т.е. переносное движение поступательное), то единичные орты будут постоянны и по модулю и по направлению и их производные по времени будут равны нулю, следовательно и ускорение Кориолиса равно нулю.
Теорема о сложении ускорений при поступательном переносном движении будет выражаться равенством:

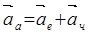 (3.9)
(3.9)
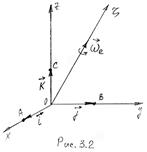
Рассмотрим переносное вращательное движение. Пусть подвижная система вращается вокруг оси О3 с угловой скоростью 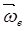 (рис. 3.2). единичные орты
(рис. 3.2). единичные орты 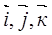 можно рассматривать как радиус-векторы точек А, В и С соответственно. А производные по времени от радиус-векторов точек дают скорости точек.
можно рассматривать как радиус-векторы точек А, В и С соответственно. А производные по времени от радиус-векторов точек дают скорости точек.
|
Следовательно:
 ;
; 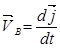 ;
; 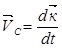 (а)
(а)
с другой стороны, скорости точек А, В и С мы можем найти как во вращательном движении по формуле (2.11):
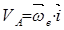 ;
;  ;
; 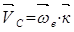 (б)
(б)
сравнивая (а) и (б) находим, что:
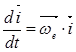 ;
;  ;
; 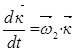 ; (в)
; (в)
Подставим эти значения в формулу (3.7)

Таким образом ускорение Кориолиса равно удвоенному векторному произведению вектора угловой скорости переносного движения на вектор относительной скорости.
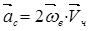 (3.10)
(3.10)
Его величина
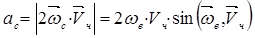 (3.11)
(3.11)
|
В соответствии с правилом векторного произведения ускорения Кориолиса направлено перпендикулярно плоскости, в которой лежат векторы 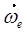 и
и 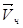 , в ту сторону, чтобы, глядя навстречу ему, мы видим поворот вектора
, в ту сторону, чтобы, глядя навстречу ему, мы видим поворот вектора 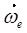 к вектору
к вектору 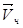 на меньший угол происходящим против часовой стрелки.
на меньший угол происходящим против часовой стрелки.
Другое правило: чтобы найти направление ускорения Кориолиса, надо вектор 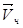 спроецировать на плоскость, перпендикулярно оси переносного вращения, и полученную проекцию повернуть на 90о в сторону вращения. Эти и будет направление вектора
спроецировать на плоскость, перпендикулярно оси переносного вращения, и полученную проекцию повернуть на 90о в сторону вращения. Эти и будет направление вектора 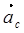 .
.
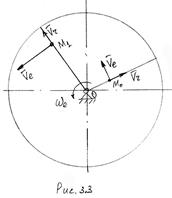
Физический смысл ускорения Кориолиса выясним на таком примере. Пусть круглая платформа вращается с постоянной угловой скоростью 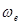 , а по радиусу платформы двигается точка М с постоянной относительной скоростью V ч (рис. 3.3). В некоторый момент точка занимает положение Мо, а через промежуток времени
, а по радиусу платформы двигается точка М с постоянной относительной скоростью V ч (рис. 3.3). В некоторый момент точка занимает положение Мо, а через промежуток времени 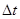 положение М1. При этом произошло изменение относительной скорости за счет переносного движения (изменилось направление вектора
положение М1. При этом произошло изменение относительной скорости за счет переносного движения (изменилось направление вектора 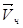 ) и изменение переносной скорости за счет относительного движения (изменилась величина
) и изменение переносной скорости за счет относительного движения (изменилась величина 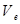 в результате удаления точки от оси вращения). Эти два изменения и характеризуются ускорением Кориолиса.
в результате удаления точки от оси вращения). Эти два изменения и характеризуются ускорением Кориолиса.
Таким образом, ускорение Кориолиса характеризует изменение относительной скорости в результате переносного движения и изменение переносной скорости в результате относительного движения.
В общем случае движения формулы (3.8) удобнее использовать в таком виде:
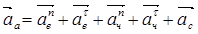 (3.12)
(3.12)
Задача кинематики плоского движения твердого тела - найти характеристики движения самого тела и отдельных его точек. В данном задании к таким характеристикам относятся векторы угловой скорости и углового ускорения тела.
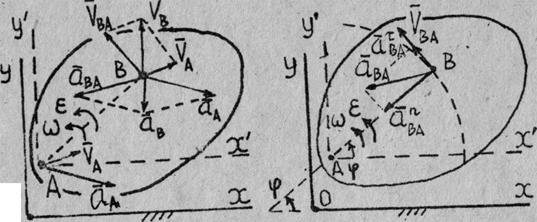
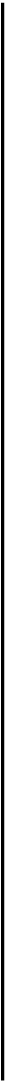 Рис. 1
Рис. 1
Основные формулы кинематики плоского движения твердого тела - векторные формулы, связывающие соответственно скорости и ускорения двух произвольных точек плоской фигуры, например, точек А и В (рис. 1)
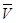 B =
B = 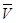 A +
A + 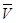 BA =
BA = 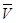 A +
A + 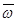 ´
´ 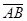 ; (1)
; (1)
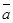 B =
B = 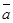 A +
A + 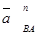 +
+ 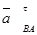 =
= 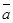 A +
A + 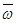 × (
× ( 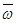 ´
´  ) +
) + 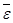 ×
×  ; (2)
; (2)
где 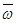 ,
, 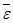 , - векторы угловой скорости и углового ускорения вращения плоской фигуры вокруг любой оси, например Az' перпендикулярной плоскости движения Oxy относительно системы координат Ax'y'z', оси которой параллельны осям неподвижной системы координат Оxyz.На рис.1 оси Оz. и Аz' не изображены, так как считается, что они перпендикулярны к плоскости рисунка и направлены на наблюдателя, а плоскости Охy и Аx'y' совпадают с плоскостью рисунка.
, - векторы угловой скорости и углового ускорения вращения плоской фигуры вокруг любой оси, например Az' перпендикулярной плоскости движения Oxy относительно системы координат Ax'y'z', оси которой параллельны осям неподвижной системы координат Оxyz.На рис.1 оси Оz. и Аz' не изображены, так как считается, что они перпендикулярны к плоскости рисунка и направлены на наблюдателя, а плоскости Охy и Аx'y' совпадают с плоскостью рисунка.
Левые части выражений
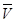 BA =
BA = 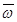 ´
´ 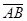 ;
;  =
= 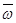 × (
× ( 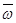 ´
´ 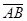 ) =
) = 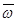 ×
× 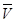 BA;
BA;  =
= 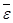 ×
×  ;
;
являются соответственно векторами скорости, нормального и касательного ускорения точки В относительно системы координат Ax'y'z' при вращении отрезка АВ в плоскости рисунка вокруг точки A, называемой в таком случае полюсом, с угловой скоростью 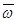 и угловым ускорением
и угловым ускорением  . Индексы n и t , в выражениях
. Индексы n и t , в выражениях 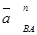 и
и 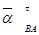 указывают, что эти векторы направлены соответственно по внутренней нормали и касательной в точке B к окружности радиуса r = AB с центром в точке А. Модули упомянутых векторов
указывают, что эти векторы направлены соответственно по внутренней нормали и касательной в точке B к окружности радиуса r = AB с центром в точке А. Модули упомянутых векторов 
 находятся по формулам
находятся по формулам
½ 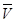 BA½ =
BA½ =  ´ AB; ½
´ AB; ½ 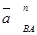 ½ =
½ = 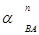 =
= 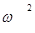 ´ AB; ½
´ AB; ½ 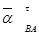 ½ =
½ = 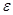 ´ AB; (3)
´ AB; (3)
Векторы 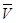 BA,
BA, 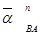 ,
, 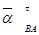 лежат в плоскости движения плоской фигуры тела, причем ненулевые векторы
лежат в плоскости движения плоской фигуры тела, причем ненулевые векторы 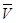 BA,
BA, 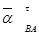 перпендикулярны отрезку AB, а ненулевой вектор
перпендикулярны отрезку AB, а ненулевой вектор 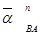 направлен от точки В к точке А . Таким образом, для этих векторов всегда известны линии действия.
направлен от точки В к точке А . Таким образом, для этих векторов всегда известны линии действия.
Поскольку модуль ускорения 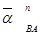 может быть вычислен по формуле (3) через угловую скорость тела
может быть вычислен по формуле (3) через угловую скорость тела  , обычно известную к этапу нахождения ускорений, целесообразно в формуле (2) вектор
, обычно известную к этапу нахождения ускорений, целесообразно в формуле (2) вектор 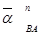 записывать вслед за известным вектором
записывать вслед за известным вектором 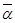 А, т.е. перед вектором
А, т.е. перед вектором 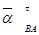 .
.
Векторы 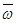 и
и 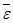 параллельны оси Оz и поэтому полностью определяются своими проекциями на эту ось
параллельны оси Оz и поэтому полностью определяются своими проекциями на эту ось
Модуль проекции равен модулю вектора 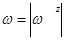 ;
; 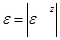 , а знак проекции указывает на направление вектора. Например, если проекции векторов положительны (
, а знак проекции указывает на направление вектора. Например, если проекции векторов положительны ( 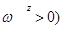 , то векторы
, то векторы 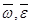 направлены так же, как и
направлены так же, как и 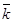 , или ось Oz. Таким образом, при плоском движении тела задача нахождения векторов
, или ось Oz. Таким образом, при плоском движении тела задача нахождения векторов 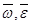 сводится к задаче отыскания их проекций на ось Oz или Az'.
сводится к задаче отыскания их проекций на ось Oz или Az'.
Если 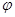 (рад) - угол между осью Ax' (Ох) и вектором
(рад) - угол между осью Ax' (Ох) и вектором 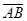 (рис. 1) и за положительное направление отсчета угла
(рис. 1) и за положительное направление отсчета угла  для выбранной системы координат принято направление против хода часовой стрелки, то
для выбранной системы координат принято направление против хода часовой стрелки, то
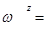
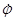 рад/с;
рад/с; 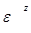 =
= 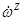
 =
= 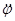
 рад/с. (4)
рад/с. (4)
О направлении векторов 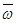 и
и 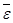 судят по круговым стрелкам
судят по круговым стрелкам 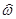 и
и 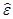 согласно правилу: "круговая стрелка, направленная против хода стрелки часов, соответствует вектору, направленному так же, как ось Oz".
согласно правилу: "круговая стрелка, направленная против хода стрелки часов, соответствует вектору, направленному так же, как ось Oz".
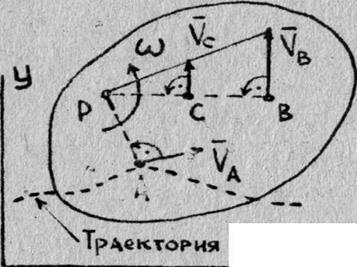
Из формул, использующих понятие МЦС (точка Р) на рис.2,
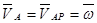 ´
´ 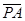 ;
; 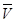 B =
B = 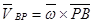 ;
; 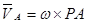 ;
;
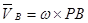 ;
; 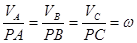 , (5)
, (5)
следует, что в данный момент времени распределение скоростей точек тела при плоском движении таково, как если бы тело вращалось вокруг оси Рz с угловой скоростью 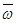 .
.
|
|


 Если отсчитывать угол 90 от направления вектора скорости точки
Если отсчитывать угол 90 от направления вектора скорости точки  A к направлению АР от этой точки до МЦС, то направление отсчета угла совпадает с направлением круговой стрелки
A к направлению АР от этой точки до МЦС, то направление отсчета угла совпадает с направлением круговой стрелки 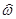 . Этот факт можно использовать для определения направления вектора
. Этот факт можно использовать для определения направления вектора 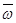 .
.
Из формул, использующих понятие МЦУ (точка Q на рис. 3),
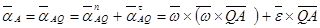
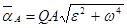 ;
; 
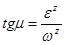 ; (6)
; (6)
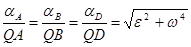 ,
,
следует, что в данный момент времени распределение ускорений точек тела при плоском движении таково, как если бы тело вращалось вокруг оси Qz с угловой скоростью 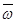 и угловым ускорением
и угловым ускорением 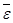 .
.
Угол 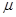 отсчитывается от вектора ускорения какой-либо точки в направлении круговой стрелки
отсчитывается от вектора ускорения какой-либо точки в направлении круговой стрелки 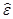 . При отыскании положения МЦУ по ускорениям двух точек, например по
. При отыскании положения МЦУ по ускорениям двух точек, например по 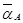 и
и 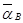 , под углом
, под углом 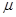 к соответствующим ускорениям проводят лучи AQ и BQ. Точка пересечения лучей (точка Q) является МЦУ плоской фигуры в данный момент времени.
к соответствующим ускорениям проводят лучи AQ и BQ. Точка пересечения лучей (точка Q) является МЦУ плоской фигуры в данный момент времени.
Направления векторов 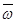 и
и  помимо формул (4) могут быть найдены из отдельных векторных формул
помимо формул (4) могут быть найдены из отдельных векторных формул
 ;
; 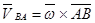 ;
; 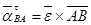 . (7)
. (7)
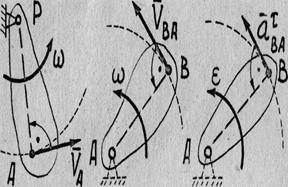
Рис. 4
Чтобы избежать анализа расположения трех взаимно перпендикулярных векторов формул (7) при известных  ,
, 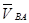 ,
, 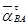 направления
направления 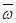 и
и 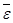 находят аналогично случаю вращательного движения тела вокруг неподвижной оси (рис. 4).
находят аналогично случаю вращательного движения тела вокруг неподвижной оси (рис. 4).

Рис. 5 
Кинематика плоского движения
катка радиуса R. при отсутствии скольжения по направляющей (в общем случае криволинейной), имеет некоторые особенности вследствие того, что мгновенный центр скоростей катка (точка Р ) совпадает с точкой окружности касающейся направляющей (рис. 5). Поэтому при движении катка расстояние от его центра (точки А) до МЦС является неизменным во времени и равным R.
AP(t) = const = R (8)
Свойство неизменности расстояния АР позволяет установить дополнительные соотношения, удобные для расчетов кинематических характеристик катка. Представим вектор скорости точки А с помощью:
а) формулы естественного способа задания движения точки
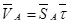 , где
, где 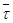 - единичный вектор естественного трехгранника, касательный в точке A к кривой ее движения; SA - криволинейная координата точки;
- единичный вектор естественного трехгранника, касательный в точке A к кривой ее движения; SA - криволинейная координата точки;
б) формулы (7) плоского движения тела
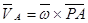 ,
,
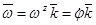 ;
;
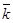 - орт оси Оz, перпендикулярной плоскости движения катка Qxy; j - угол, задающий направление какого-либо отрезка плоской фигуры катка. Ввиду произвольности выбора такого отрезка, обычно собственно отрезок, не указывают на рисунках, а изображают лишь круговую стрелку положительного направления отсчета угла j, называя его углом поворота катка.
- орт оси Оz, перпендикулярной плоскости движения катка Qxy; j - угол, задающий направление какого-либо отрезка плоской фигуры катка. Ввиду произвольности выбора такого отрезка, обычно собственно отрезок, не указывают на рисунках, а изображают лишь круговую стрелку положительного направления отсчета угла j, называя его углом поворота катка.
Дата: 2019-07-30, просмотров: 274.