ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
К курсовой работе
по дисциплине «Теория автоматического управления»
На тему «Динамический расчет следящих систем»
Вариант 5, колонка 1.
Выполнил:
студент гр. А-144
18.12.07 г
Безродный С.В.
Проверил:
преподаватель кафедры САУ
18.12.07 г
Гайдук А.Р.
Таганрог 2007 г.
СОДЕРЖАНИЕ.
1.ВВЕДЕНИЕ. 3
2.ТЕХНИЧЕСКОЕ ЗАДАНИЕ. 5
3.ОПИСАНИЕ СЛЕДЯЩЕЙ СИСТЕМЫ. 7
4. УРАВНЕНИЯ ЭЛЕМЕНТОВ. 8
4.1 Измеритель рассогласования. 8
4.2 Датчик выхода. 9
4.3 Усилитель мощности. 10
4.4 Редуктор. 10
4.5 Двигатель постоянного тока. 11
5.ВЫВОД УРАВНЕНИЙ СИСТЕМЫ. 15
5.1 Уравнения в переменных состояния. 15
5.2 Матричная форма уравнений в переменных состояния. 15
5.3 Уравнения вход-выход заданной части системы. 16
6.АНАЛИЗ СВОЙСТВ ЗАДАННОЙ ЧАСТИ СЛЕДЯЩЕЙ СИСТЕМЫ. 18
6.1 Проверка управляемости. 18
6.2 Проверка наблюдаемости заданной части системы. 19
6.3 Проверка устойчивости нескорректированной системы. 20
7. СИНТЕЗ УСТРОЙСТВА УПРАВЛЕНИЯ. 22
8. СИНТЕЗ НАБЛЮДАТЕЛЯ ПЕРЕМЕННЫХ СОСТОЯНИЯ. 25
9. ПОСТРОЕНИЕ И АНАЛИЗ МОДЕЛИ СИСТЕМЫ. 27
10.ЗАКЛЮЧЕНИЕ. 35
11.СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ. 36
ПРИЛОЖЕНИЕ. Схема электрическая принципиальная.
ВВЕДЕНИЕ.
В зависимости от характера информации, получаемой об объекте в процессе его работы, наличия его математического описания, статических характеристик объекта и главное – задачи, поставленной перед системой автоматического управления, принципы автоматического управления существенно различаются.
Основной задачей курсовой работы является синтез и последующее исследование следящей системы с использованием современных методов и инструментов теории управления. Основным требованием, предъявляемым к следящим системам, является минимум погрешности 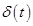 , определяемой как разность между заранее неизвестным законом
, определяемой как разность между заранее неизвестным законом 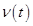 и управляемой величиной
и управляемой величиной 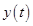 . Следящая система представляет собой замкнутую систему регулирования угла поворота вала, управляемого двигателем; задающее воздействие устанавливается путем поворота некоторого задающего вала.
. Следящая система представляет собой замкнутую систему регулирования угла поворота вала, управляемого двигателем; задающее воздействие устанавливается путем поворота некоторого задающего вала.
Выполнение данной курсовой работы охватывает следующие разделы курса «Теория управления»: «Составление математических моделей элементов систем и регулярных воздействий»; «Преобразование моделей»; «Аналитический синтез уравнений управляющего устройства по требованиям к качеству системы»; реализация этих уравнений, т.е. разработка схемы устройства управления или алгоритма работы цифрового варианта устройства управления.
Следящие системы применяются для управления радиолокационными антеннами, радиотелескопами, артиллерийскими установками на подвижных платформах, а также для регулирования синхронности и синфазности вращения валов ведущего и ведомого двигателей в том случае, когда они расположены на достаточно большом расстоянии друг от друга.
Нетрудно заметить, что качественные следящие системы, отрабатывающие с заданной точностью поступающие на их вход задающие воздействия, применяются во многих сферах жизнедеятельности людей: в промышленности, в области военной техники, в гражданской авиации и т.д. Однако создание следящих систем, которые затем найдут свое применение в определенных областях человеческой деятельности, включает в себя несколько этапов: постановку задачи, разработку математической модели синтезируемой системы, непосредственно синтез самой системы и переход от математической модели проектируемой системы к реальным устройствам, которые бы описывались синтезированной моделью, т.е. этап реализации. В данной курсовой работе как раз и рассматриваются все перечисленные этапы создания следящих систем.
ТЕХНИЧЕСКОЕ ЗАДАНИЕ.
1) Начертить функциональную схему заданной части системы, вывести дифференциальные уравнения в переменных состояния всех элементов, а также заданной части системы. Численные значения параметров элементов системы:
| Параметр | Величина |
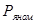 , Вт , Вт
| 77 |
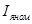 , А , А
| 1,2 |
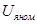 , В , В
| 110 |
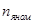 , об/мин , об/мин
| 3000 |
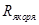 , Ом , Ом
| 5,1 |
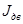 , кг·м2 , кг·м2
| 25·10-4 |
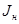 , кг·м·с2 , кг·м·с2
| 0,28 |

| 75 |
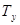 , с , с
| 0,035 |
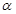 , В/град , В/град
| 1 |
Тип усилителя – транзисторный.
Тип измерителя рассогласования – сельсины.
2) Проверить наблюдаемость, управляемость и устойчивость заданной части при коэффициенте усиления усилителя 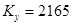 .
.
3) Начертить структурную расчетную схему заданной части, вывести уравнения вход-выход заданной части системы.
4) Построить модальное управление по заданному времени регулирования 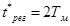 и условию астатизма первого порядка.
и условию астатизма первого порядка.
5) Построить наблюдатель Калмана для заданной части системы, перейти к управлению по оценкам переменных состояния, время переходного процесса в наблюдателе положить равным 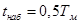 .
.
6) Проверить устойчивость замкнутой системы, построить переходные характеристики 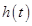 , воспользовавшись для моделирования пакетом SIMULINK for Windows в системе MatLAB.
, воспользовавшись для моделирования пакетом SIMULINK for Windows в системе MatLAB.
7) Осуществить выбор электрической схемы усилителя мощности (по литературным источникам), построить схему управляющего устройства вместе с наблюдателем на операционных усилителях и схему всей системы.
ОПИСАНИЕ СЛЕДЯЩЕЙ СИСТЕМЫ.
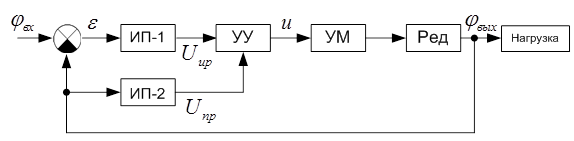
Рис.1. Функциональная схема проектируемой системы.
ИП-1 – измерительный преобразователь (сельсины)
ИП-2 – потенциометрический преобразователь угла поворота выходного вала
УУ – управляющее устройство
УМ – усилитель мощности
ИД – исполнительный двигатель
Ред – редуктор
Нагрузка – приводимый в движение рассматриваемой системой агрегат
В качестве измерительных преобразователей (чувствительных элементов) используются сельсины. Преобразователь угла поворота выходного вала ИП-2 берется потенциометрическим. Потенциометрические датчики обычно питаются от источника постоянного напряжения. Если измерительные преобразователи работают на переменном токе, то на их выходе включается фазочувствительный усилитель-выпрямитель, являющийся составной частью соответствующего ИП, т.е. его коэффициент передачи учтен в заданном коэффициенте передачи чувствительного элемента.
Управляющее устройство (УУ), принимает сигналы, поступающие с обоих ИП. В нем формируется напряжение, пропорциональное управляющему воздействию, которое затем подается на усилитель мощности (УМ). В курсовой работе синтезируется уравнение УУ и разрабатывается его схема на операционных усилителях.
УРАВНЕНИЯ ЭЛЕМЕНТОВ
Измеритель рассогласования.
В данной системе используется измеритель рассогласования на сельсинах, схема которого изображена на рисунке 2.
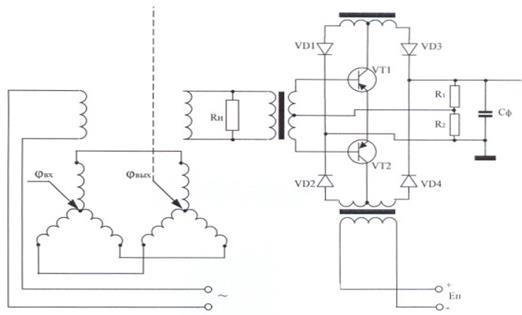
Рис.2. Схема измерителя рассогласования на сельсинах с фазочувствительным усилителем.
Измеритель рассогласования следует считать безынерционным, так как его постоянная времени на несколько порядков меньше постоянных времени остальных звеньев.
 ,
, 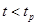
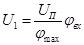 ,
,
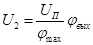 ,
,
Уравнение измерителя рассогласования:
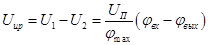 , (1)
, (1)
где 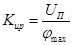 - коэффициент передачи измерителя рассогласования.
- коэффициент передачи измерителя рассогласования.
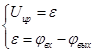 (2)
(2)
Уравнение в переменных состояния и уравнение вход-выход совпадают, так как данный элемент является безынерционным.
Сельсины являются индукционными машинами, которые позволяют при постоянном напряжении на выходе получать на выходных обмотках систему напряжений, амплитуда и фаза которых определяются угловым положением ротора. Сельсины также позволяют преобразовать такую систему напряжений в соответствующее ей угловое положение ротора или в напряжение, фаза и амплитуда которого являются функцией системы входных напряжений и угла поворота ротора. Поэтому сельсины часто применяются в качестве измерителей рассогласования следящих систем.
Датчик выхода.
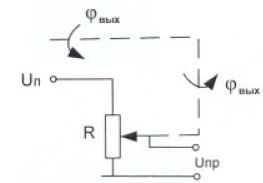
Рис.3. Схема датчика выхода.
Этот датчик угла поворота вала нагрузки описывается уравнением:
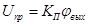 , (3)
, (3)
где 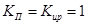 .
.
Усилитель мощности.
Так как по заданию усилитель мощности является звеном первого порядка, то его уравнение имеет вид:
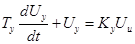 (4)
(4)
это уравнение вход-выход.
Обозначим 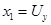 , получим следующую систему:
, получим следующую систему:
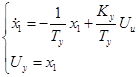 (5)
(5)
это уравнение усилителя.
Передаточная функция усилителя может быть записана в виде:
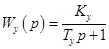 (6)
(6)
Подставляя исходные значения 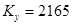 ,
, 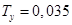 , получим:
, получим:
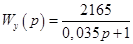 (7)
(7)
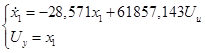 (8)
(8)
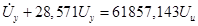 (9)
(9)
Редуктор.
По техническому заданию инерционность редуктора учитывается в уравнении двигателя, поэтому редуктор считается безынерционным звеном и его уравнение имеет вид:
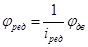
Уравнение вход-выход и уравнение в переменных состояния:
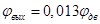
Передаточная функция редуктора:
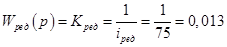
Двигатель постоянного тока.
Управление осуществляется по цепи якоря, магнитный поток в зазоре постоянный, а реакция якоря и гистерезис магнитной цепи отсутствует. В этом случае исходные уравнения двигателя оказываются линейными и образуют следующую систему уравнений:
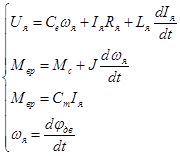 (10)
(10)
Здесь 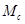 – приведенный к валу двигателя момент сопротивления;
– приведенный к валу двигателя момент сопротивления;
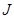 – приведенный к валу двигателя момент инерции вращающихся частей;
– приведенный к валу двигателя момент инерции вращающихся частей;
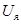 – напряжение, приложенное к якорю двигателя;
– напряжение, приложенное к якорю двигателя;
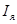 ,
, 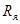 ,
, 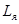 ,
, 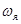 – ток, сопротивление, индуктивность и угловая скорость цепи якоря;
– ток, сопротивление, индуктивность и угловая скорость цепи якоря;
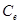 ,
, 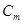 – конструктивные постоянные двигателя;
– конструктивные постоянные двигателя;
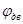 – угол поворота вала двигателя.
– угол поворота вала двигателя.
Установившийся режим работы двигателя:
Значения переменных в этом режиме будем обозначать с нулевыми индексами:
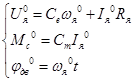 (11)
(11)
Эти уравнения можно использовать для определения коэффициентов 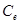 и
и 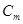 , так как один из установившихся режимов называется номинальным и соответствует значениям:
, так как один из установившихся режимов называется номинальным и соответствует значениям:
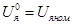 ,
, 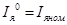 ,
, 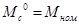 ,
,
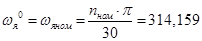 (рад/с)
(рад/с)
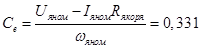
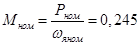
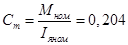
Модель двигателя необходимо получить в отклонениях от установившегося режима, но поскольку уравнение (10) линейное, то уравнения в отклонениях будут иметь вид (10).
Вывод динамической модели:
Так как индукция якоря учтена в постоянной времени усилителя мощности, то в (10) индукция равна нулю. Отсюда можно найти ток якоря:
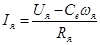
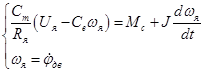 (12)
(12)
Обозначим 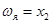 ,
, 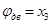 и получим уравнения в переменных состояния:
и получим уравнения в переменных состояния:
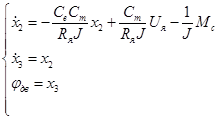 (13)
(13)
Для того, чтобы получить уравнение вход-выход необходимо продифференцировать второе уравнение системы по времени.
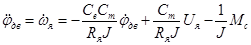
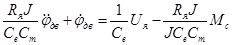 , (14)
, (14)
где 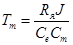 – электромеханическая постоянная двигателя;
– электромеханическая постоянная двигателя;
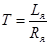 – электромагнитная постоянная двигателя;
– электромагнитная постоянная двигателя;
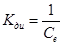 ,
, 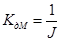 .
.
Уравнение двигателя принимает вид:
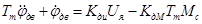 (15)
(15)
Расчет коэффициентов:
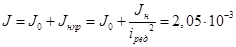 (кг·м2)
(кг·м2)
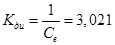
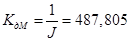
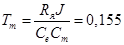
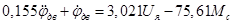 (16)
(16)
Передаточная функция двигателя:
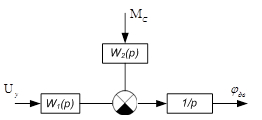
Рис.4.Структурная схема двигателя.
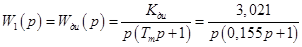 ; (17)
; (17)
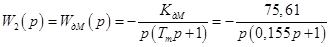 .
.
ВЫВОД УРАВНЕНИЙ СИСТЕМЫ.
Проверка управляемости.
Проверку проводим по уравнению (18) при 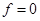 с помощью критерия управляемости.
с помощью критерия управляемости.
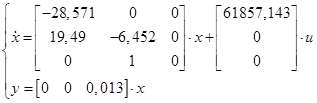
Обычно предполагают, что объект управления (система) обеспечивает возможность изменения его переменных состояния и регулируемых величин в соответствие с целью управления с помощью управлений, приложенных к нему. Однако ясно, что в общем случае не всякий объект управления допускает такую возможность, т.е. не каждый объект является управляемым. Следует отметить, что это свойство – управляемости – зависит исключительно от внутренних свойств объекта.
Для оценки управляемости систем используется критерий Калмана, в основе которого лежит матрица управляемости:
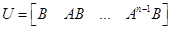 ,
,
где 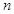 - размерность вектора переменных состояния.
- размерность вектора переменных состояния.
В нашем случае 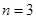 , значит:
, значит:
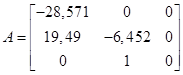 ,
, 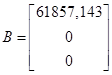 ,
,
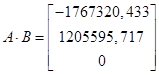 ,
,
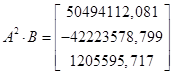
Матрица U будет иметь вид:
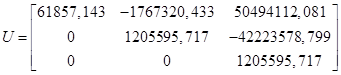
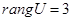
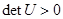
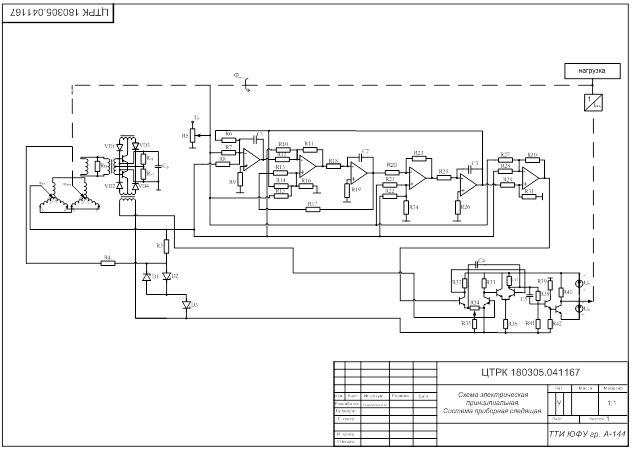
Так как 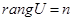 и определитель матрицы U не равен нулю, то объект является полностью управляемым.
и определитель матрицы U не равен нулю, то объект является полностью управляемым.
ЗАКЛЮЧЕНИЕ.
В данной курсовой работе была синтезирована и исследована с использованием современных методов и инструментов теории управления приборная следящая система.
Данная курсовая работа выполнена с помощью программного пакета SIMULINK в системе MATLAB (для проведения численного моделирования) и программы MathCAD (для выполнения расчётов).
В данной курсовой работе было синтезировано устройство управления, для этого выведены дифференциальные уравнения в переменных состояния всех элементов, а также заданной части системы; проверены наблюдаемость, управляемость и устойчивость заданной части; построена структурная расчётная схема, выведены уравнения вход-выход; построено модальное управление и наблюдатель Калмана; проделано моделирование с помощью SIMULINK в системе MATLAB, а также была построена схема управляющего устройства вместе с наблюдателем на операционных усилителях.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ.
1. Теория автоматического управления. Под ред. А. В. Нетушила. Учебник для вузов. Изд. 2-е. М., "Высшая школа",1976.
2. Гайдук А. Р., Пьявченко Т. А. Учебно-методическое пособие по выполнению курсовой работы «Динамический расчет следящих систем» по дисциплине «Теория управления». Таганрог: Изд-во ТРТУ, 2001. 19с.
3. А. Р. Гайдук. Алгебраические методы анализа и синтеза систем автоматического управления. Ростов-на-Дону: Изд-во РГУ, 1988. 208с.
4. Принципы регулирования. Руководство к лабораторной работе по курсу "Теория автоматического управления"/Таганрог. Радиотехнический институт; Сост. Н. В. Балалаев, Ю. Г. Сотников; Таганрог. 1993. 20 с.
ПРИЛОЖЕНИЕ. Схема электрическая принципиальная.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
К курсовой работе
по дисциплине «Теория автоматического управления»
на тему «Динамический расчет следящих систем»
Вариант 5, колонка 1.
Выполнил:
студент гр. А-144
18.12.07 г
Безродный С.В.
Проверил:
преподаватель кафедры САУ
18.12.07 г
Гайдук А.Р.
Таганрог 2007 г.
СОДЕРЖАНИЕ.
1.ВВЕДЕНИЕ. 3
2.ТЕХНИЧЕСКОЕ ЗАДАНИЕ. 5
3.ОПИСАНИЕ СЛЕДЯЩЕЙ СИСТЕМЫ. 7
4. УРАВНЕНИЯ ЭЛЕМЕНТОВ. 8
4.1 Измеритель рассогласования. 8
4.2 Датчик выхода. 9
4.3 Усилитель мощности. 10
4.4 Редуктор. 10
4.5 Двигатель постоянного тока. 11
5.ВЫВОД УРАВНЕНИЙ СИСТЕМЫ. 15
5.1 Уравнения в переменных состояния. 15
5.2 Матричная форма уравнений в переменных состояния. 15
5.3 Уравнения вход-выход заданной части системы. 16
6.АНАЛИЗ СВОЙСТВ ЗАДАННОЙ ЧАСТИ СЛЕДЯЩЕЙ СИСТЕМЫ. 18
6.1 Проверка управляемости. 18
6.2 Проверка наблюдаемости заданной части системы. 19
6.3 Проверка устойчивости нескорректированной системы. 20
7. СИНТЕЗ УСТРОЙСТВА УПРАВЛЕНИЯ. 22
8. СИНТЕЗ НАБЛЮДАТЕЛЯ ПЕРЕМЕННЫХ СОСТОЯНИЯ. 25
9. ПОСТРОЕНИЕ И АНАЛИЗ МОДЕЛИ СИСТЕМЫ. 27
10.ЗАКЛЮЧЕНИЕ. 35
11.СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ. 36
ПРИЛОЖЕНИЕ. Схема электрическая принципиальная.
ВВЕДЕНИЕ.
В зависимости от характера информации, получаемой об объекте в процессе его работы, наличия его математического описания, статических характеристик объекта и главное – задачи, поставленной перед системой автоматического управления, принципы автоматического управления существенно различаются.
Основной задачей курсовой работы является синтез и последующее исследование следящей системы с использованием современных методов и инструментов теории управления. Основным требованием, предъявляемым к следящим системам, является минимум погрешности 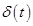 , определяемой как разность между заранее неизвестным законом
, определяемой как разность между заранее неизвестным законом 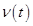 и управляемой величиной
и управляемой величиной 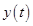 . Следящая система представляет собой замкнутую систему регулирования угла поворота вала, управляемого двигателем; задающее воздействие устанавливается путем поворота некоторого задающего вала.
. Следящая система представляет собой замкнутую систему регулирования угла поворота вала, управляемого двигателем; задающее воздействие устанавливается путем поворота некоторого задающего вала.
Выполнение данной курсовой работы охватывает следующие разделы курса «Теория управления»: «Составление математических моделей элементов систем и регулярных воздействий»; «Преобразование моделей»; «Аналитический синтез уравнений управляющего устройства по требованиям к качеству системы»; реализация этих уравнений, т.е. разработка схемы устройства управления или алгоритма работы цифрового варианта устройства управления.
Следящие системы применяются для управления радиолокационными антеннами, радиотелескопами, артиллерийскими установками на подвижных платформах, а также для регулирования синхронности и синфазности вращения валов ведущего и ведомого двигателей в том случае, когда они расположены на достаточно большом расстоянии друг от друга.
Нетрудно заметить, что качественные следящие системы, отрабатывающие с заданной точностью поступающие на их вход задающие воздействия, применяются во многих сферах жизнедеятельности людей: в промышленности, в области военной техники, в гражданской авиации и т.д. Однако создание следящих систем, которые затем найдут свое применение в определенных областях человеческой деятельности, включает в себя несколько этапов: постановку задачи, разработку математической модели синтезируемой системы, непосредственно синтез самой системы и переход от математической модели проектируемой системы к реальным устройствам, которые бы описывались синтезированной моделью, т.е. этап реализации. В данной курсовой работе как раз и рассматриваются все перечисленные этапы создания следящих систем.
ТЕХНИЧЕСКОЕ ЗАДАНИЕ.
1) Начертить функциональную схему заданной части системы, вывести дифференциальные уравнения в переменных состояния всех элементов, а также заданной части системы. Численные значения параметров элементов системы:
| Параметр | Величина |
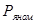 , Вт , Вт
| 77 |
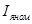 , А , А
| 1,2 |
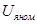 , В , В
| 110 |
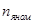 , об/мин , об/мин
| 3000 |
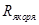 , Ом , Ом
| 5,1 |
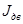 , кг·м2 , кг·м2
| 25·10-4 |
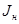 , кг·м·с2 , кг·м·с2
| 0,28 |

| 75 |
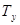 , с , с
| 0,035 |
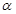 , В/град , В/град
| 1 |
Тип усилителя – транзисторный.
Тип измерителя рассогласования – сельсины.
2) Проверить наблюдаемость, управляемость и устойчивость заданной части при коэффициенте усиления усилителя 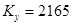 .
.
3) Начертить структурную расчетную схему заданной части, вывести уравнения вход-выход заданной части системы.
4) Построить модальное управление по заданному времени регулирования 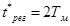 и условию астатизма первого порядка.
и условию астатизма первого порядка.
5) Построить наблюдатель Калмана для заданной части системы, перейти к управлению по оценкам переменных состояния, время переходного процесса в наблюдателе положить равным 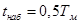 .
.
6) Проверить устойчивость замкнутой системы, построить переходные характеристики 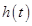 , воспользовавшись для моделирования пакетом SIMULINK for Windows в системе MatLAB.
, воспользовавшись для моделирования пакетом SIMULINK for Windows в системе MatLAB.
7) Осуществить выбор электрической схемы усилителя мощности (по литературным источникам), построить схему управляющего устройства вместе с наблюдателем на операционных усилителях и схему всей системы.
ОПИСАНИЕ СЛЕДЯЩЕЙ СИСТЕМЫ.

Рис.1. Функциональная схема проектируемой системы.
ИП-1 – измерительный преобразователь (сельсины)
ИП-2 – потенциометрический преобразователь угла поворота выходного вала
УУ – управляющее устройство
УМ – усилитель мощности
ИД – исполнительный двигатель
Ред – редуктор
Нагрузка – приводимый в движение рассматриваемой системой агрегат
В качестве измерительных преобразователей (чувствительных элементов) используются сельсины. Преобразователь угла поворота выходного вала ИП-2 берется потенциометрическим. Потенциометрические датчики обычно питаются от источника постоянного напряжения. Если измерительные преобразователи работают на переменном токе, то на их выходе включается фазочувствительный усилитель-выпрямитель, являющийся составной частью соответствующего ИП, т.е. его коэффициент передачи учтен в заданном коэффициенте передачи чувствительного элемента.
Управляющее устройство (УУ), принимает сигналы, поступающие с обоих ИП. В нем формируется напряжение, пропорциональное управляющему воздействию, которое затем подается на усилитель мощности (УМ). В курсовой работе синтезируется уравнение УУ и разрабатывается его схема на операционных усилителях.
УРАВНЕНИЯ ЭЛЕМЕНТОВ
Измеритель рассогласования.
В данной системе используется измеритель рассогласования на сельсинах, схема которого изображена на рисунке 2.

Рис.2. Схема измерителя рассогласования на сельсинах с фазочувствительным усилителем.
Измеритель рассогласования следует считать безынерционным, так как его постоянная времени на несколько порядков меньше постоянных времени остальных звеньев.
 ,
, 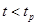
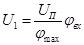 ,
,
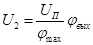 ,
,
Уравнение измерителя рассогласования:
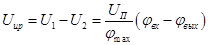 , (1)
, (1)
где 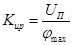 - коэффициент передачи измерителя рассогласования.
- коэффициент передачи измерителя рассогласования.
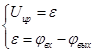 (2)
(2)
Уравнение в переменных состояния и уравнение вход-выход совпадают, так как данный элемент является безынерционным.
Сельсины являются индукционными машинами, которые позволяют при постоянном напряжении на выходе получать на выходных обмотках систему напряжений, амплитуда и фаза которых определяются угловым положением ротора. Сельсины также позволяют преобразовать такую систему напряжений в соответствующее ей угловое положение ротора или в напряжение, фаза и амплитуда которого являются функцией системы входных напряжений и угла поворота ротора. Поэтому сельсины часто применяются в качестве измерителей рассогласования следящих систем.
Датчик выхода.

Рис.3. Схема датчика выхода.
Этот датчик угла поворота вала нагрузки описывается уравнением:
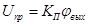 , (3)
, (3)
где 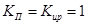 .
.
Усилитель мощности.
Так как по заданию усилитель мощности является звеном первого порядка, то его уравнение имеет вид:
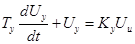 (4)
(4)
это уравнение вход-выход.
Обозначим 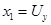 , получим следующую систему:
, получим следующую систему:
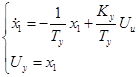 (5)
(5)
это уравнение усилителя.
Передаточная функция усилителя может быть записана в виде:
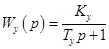 (6)
(6)
Подставляя исходные значения 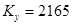 ,
, 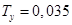 , получим:
, получим:
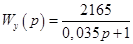 (7)
(7)
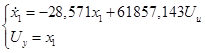 (8)
(8)
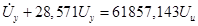 (9)
(9)
Редуктор.
По техническому заданию инерционность редуктора учитывается в уравнении двигателя, поэтому редуктор считается безынерционным звеном и его уравнение имеет вид:
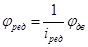
Уравнение вход-выход и уравнение в переменных состояния:
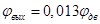
Передаточная функция редуктора:
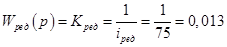
Двигатель постоянного тока.
Управление осуществляется по цепи якоря, магнитный поток в зазоре постоянный, а реакция якоря и гистерезис магнитной цепи отсутствует. В этом случае исходные уравнения двигателя оказываются линейными и образуют следующую систему уравнений:
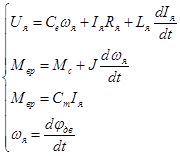 (10)
(10)
Здесь 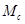 – приведенный к валу двигателя момент сопротивления;
– приведенный к валу двигателя момент сопротивления;
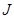 – приведенный к валу двигателя момент инерции вращающихся частей;
– приведенный к валу двигателя момент инерции вращающихся частей;
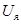 – напряжение, приложенное к якорю двигателя;
– напряжение, приложенное к якорю двигателя;
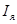 ,
, 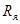 ,
, 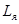 ,
, 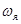 – ток, сопротивление, индуктивность и угловая скорость цепи якоря;
– ток, сопротивление, индуктивность и угловая скорость цепи якоря;
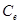 ,
, 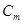 – конструктивные постоянные двигателя;
– конструктивные постоянные двигателя;
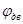 – угол поворота вала двигателя.
– угол поворота вала двигателя.
Установившийся режим работы двигателя:
Значения переменных в этом режиме будем обозначать с нулевыми индексами:
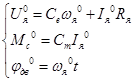 (11)
(11)
Эти уравнения можно использовать для определения коэффициентов 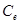 и
и 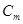 , так как один из установившихся режимов называется номинальным и соответствует значениям:
, так как один из установившихся режимов называется номинальным и соответствует значениям:
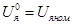 ,
, 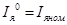 ,
, 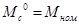 ,
,
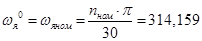 (рад/с)
(рад/с)
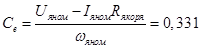
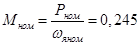
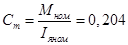
Модель двигателя необходимо получить в отклонениях от установившегося режима, но поскольку уравнение (10) линейное, то уравнения в отклонениях будут иметь вид (10).
Вывод динамической модели:
Так как индукция якоря учтена в постоянной времени усилителя мощности, то в (10) индукция равна нулю. Отсюда можно найти ток якоря:
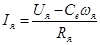
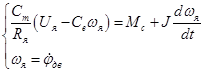 (12)
(12)
Обозначим 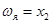 ,
, 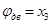 и получим уравнения в переменных состояния:
и получим уравнения в переменных состояния:
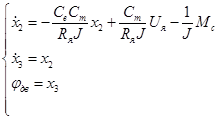 (13)
(13)
Для того, чтобы получить уравнение вход-выход необходимо продифференцировать второе уравнение системы по времени.
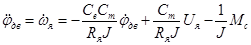
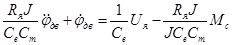 , (14)
, (14)
где 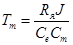 – электромеханическая постоянная двигателя;
– электромеханическая постоянная двигателя;
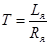 – электромагнитная постоянная двигателя;
– электромагнитная постоянная двигателя;
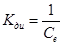 ,
, 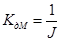 .
.
Уравнение двигателя принимает вид:
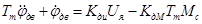 (15)
(15)
Расчет коэффициентов:
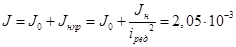 (кг·м2)
(кг·м2)
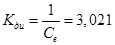
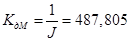
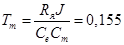
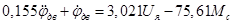 (16)
(16)
Передаточная функция двигателя:

Рис.4.Структурная схема двигателя.
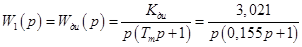 ; (17)
; (17)
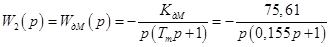 .
.
ВЫВОД УРАВНЕНИЙ СИСТЕМЫ.
Дата: 2019-07-31, просмотров: 289.