Шаг 1.
Формирование очередного подграфа Gr(r=1,2,3…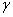 
) начинается с выбора базовой вершины 
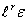из множества нераспределенных вершин Ir. В начале процесса все вершины считаются нераспределенными, т.е. Ir=E.
Критерием выбора вершины на роль базовой является ее степень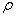 
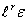( ) (под степенью вершины графа будем понимать кол-во ребер данного графа, инцидентных ей). Выбор происходит в соответствии со следующим условием:
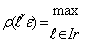
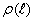(3)
Базовая вершина будет первой по порядку вершиной подграфа Gr(Er,Vr), а оставшиеся вершины, принадлежащие множеству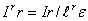 
, являются кандидатами для включения в подграф Gr на последующих шагах алгоритма.
Базовая вершина 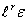является, во-первых, как бы “центром” группирования, к которому прибавляются новые вершины, во-вторых, центром факторизации.
Шаг 2.
Из множества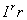 
выделяется подмножество Г ( 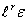) вершин, связанных с .
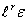Шаг 3.
Для элемента X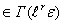 
введем функционал:
L(x)=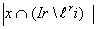 
(4)
определяющий число цепей, связывающих вершину X и вершины из множества Г и Ir\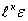 
.
Для упрощения записей будем отождествлять элемент (множество элементов). Для формального вычисления функционала будем пользоваться формулой:
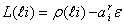(5)
где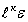 
– число связей между вершинам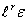и и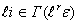 
.
Шаг 4.
Из всех вершин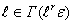 
выбирается 
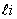такая, у которой значение функционала минимально. Очевидно, что вершина, для которой это условие будет выполняться, максимально связана с 
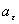. Эта вершина включается во множество Еr вершин Gr.
Множество вершин подграфа Gr приобретает следующий вид:
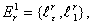(6)
где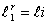 
, а верхний индекс в обозначении 
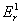в общем случае указывает кол-во шагов выборки.
Шаг 5.
Происходит стягивание вершин подграфа Gr в вершину 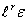. Этот процесс далее будем называть факторизацией, вершину 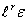– центром факторизации, а количество вершин стянутых в 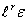, кроме него самого, – степенью факторизации.
Центр факторизации со степенью факторизации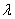 
, отличной от нуля, будем обозначать символом 
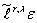и называть гипервершиной степени .
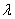После данного процесса множество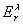 
преобразуют в одноэлементное множество 
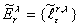содержащее гипервершину степени .
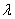В указанных обозначениях первый процесс факторизации запишется следующим образом:
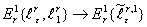. (7)
В общем случае на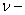 
ом шаге выборки все указанные преобразования будут иметь вид:
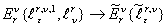. (8)
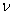=1,2,3…,Кс-1,где Кс –допустимая мощность множества вершин формируемого подграфа (кол-во элементов в конструктивном узле).
Шаг 6.
Действия, описанные в шагах 2,3,4,5, повторяются до полного заполнения формируемого модуля.
Далее весь процесс повторяется до тех пор, пока не будет сформирован ( 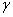-1) модуль. Последний же 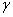–й полностью включает в себя множество 
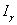, так как
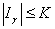. (9)
Выполнение компоновки
Данную электрическую функциональную схему распределителя уровней на 10 каналов (рис. 1) разбиваем на 3 блока. Далее выполняем компоновку для каждого блока, для чего представляем их в виде графов, где множеству вершин соответствуют элементы электрической схемы блока, а множество ребер электрическим связям между этими элементами.
Компоновка первого блока
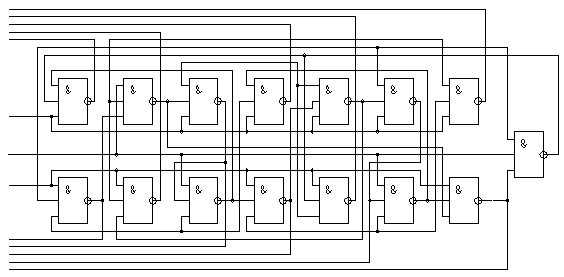
В исходной схеме выделяем однотипные логические элементы. Сведём их в блок 1.
Рис. 2. Блок 1
По блоку 1 составляем граф.
|
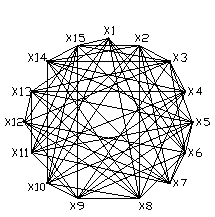
Рис. 3. Граф 1
По полученному графу составляем матрицу смежности.
Таблица 1
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | X11 | X12 | X13 | X14 | X15 | ||
| X1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 8 |
| X2 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 9 |
| X3 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 9 |
| X4 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 8 |
| X5 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 9 |
| X6 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 9 |
| X7 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 8 |
| X8 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 9 |
| X9 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 9 |
| X10 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 8 |
| X11 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 8 |
| X12 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 7 |
| X13 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 8 |
| X14 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 8 |
| X15 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 9 |
За базовую принимаем вершину X2, т.к. она имеет максимальное значение, равное 9, и минимальный порядковый номер. Она связана с вершинами X3, X4, X6, X7, X8, X10, X11, X14, X15. Посчитаем для этих вершин функционалы:
L(X1)=8-0=8, L(X3)=9-1=8, L(X4)=8-1=7, L(X5)=9-0=9,
L(X6)=9-1=8, L(X7)=8-1=7, L(X8)=9-1=8, L(X9)=9-0=9, L(X10)=8-1=7, L(X11)=8-1=7, L(X12)=7-0=7, L(X13)=8-0=8, L(X14)=8-1=7, L(X15)=9-1=8.
Стягиваем вершину X4 с базовой в первый корпус, т.к. она имеет минимальный функционал, равный 7, и минимальный порядковый номер.
Таблица 2
| X1 | X3 | X5 | X6 | X7 | X8 | X9 | X10 | X11 | X12 | X13 | X14 | X15 | ||
| X1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 |
| X3 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 2 |
| X5 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 |
| X6 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| X7 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 |
| X8 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 2 |
| X9 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 |
| X10 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 2 |
| X11 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 2 |
| X12 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| X13 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
| X14 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 2 |
| X15 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 |
| 0 | 2 | 0 | 1 | 1 | 2 | 1 | 2 | 2 | 0 | 1 | 2 | 1 | 0 |
Стягиваем вершину X7 с X4 и с базовой в первый корпус, т.к. вершина X7 также имеет функционал равный 7.
Таблица 3
| X1 | X3 | X5 | X6 | X8 | X9 | X10 | X11 | X12 | X13 | X14 | X15 | ||
| X1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| X3 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 2 |
| X5 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| X6 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 2 |
| X8 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 2 |
| X9 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 |
| X10 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 2 |
| X11 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 3 |
| X12 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
| X13 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 2 |
| X14 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 3 |
| X15 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 2 | 1 | 2 | 2 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 0 |
Так как К155ЛА4 содержит три модуля, элементы X2, X4, X7 помещаем в одну микросхему. Для оставшихся несвязанных элементов будем продолжать компоновку.
Таблица 4
| X1 | X3 | X5 | X6 | X8 | X9 | X10 | X11 | X12 | X13 | X14 | X15 | ||
| X1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 7 |
| X3 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 7 |
| X5 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 8 |
| X6 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 7 |
| X8 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 7 |
| X9 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 8 |
| X10 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 6 |
| X11 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 5 |
| X12 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 6 |
| X13 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 6 |
| X14 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 5 |
| X15 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 8 |
За базовую принимаем вершину X5, т.к. она имеет максимальное значение, равное 8, и минимальный порядковый номер. Она связана с вершинами X1, X3, X6, X9, X10, X11, X13, X14. Посчитаем для этих вершин функционалы:
L(X1)=7-1=6, L(X3)=7-1=6, L(X6)=7-1=6, L(X8)=7-0=7, L(X9)=8-1=7, L(X10)=6-1=5, L(X11)=5-1=4, L(X12)=6-0=6, L(X13)=6-1=5, L(X14)=5-1=4, L(X15)=8-0=8.
Стягиваем вершины X11, X14 с базовой во второй корпус, т.к. они имеют минимальный функционал, равный 4.
Таблица 5
| X1 | X3 | X6 | X8 | X9 | X10 | X12 | X13 | X15 | ||
| X1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 2 |
| X3 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 2 |
| X6 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| X8 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 |
| X9 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 2 |
| X10 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 2 |
| X12 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| X13 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 2 |
| X15 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 2 |
| 2 | 2 | 1 | 1 | 2 | 2 | 0 | 2 | 2 | 0 |
Так как К155ЛА4 содержит три модуля, элементы X5, X11, X14 помещаем в одну микросхему. Для оставшихся несвязанных элементов будем продолжать компоновку.
Таблица 6
| X1 | X3 | X6 | X8 | X9 | X10 | X12 | X13 | X15 | ||
| X1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 5 |
| X3 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 5 |
| X6 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 6 |
| X8 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 6 |
| X9 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 6 |
| X10 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 4 |
| X12 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 6 |
| X13 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 4 |
| X15 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 6 |
За базовую принимаем вершину X6, т.к. она имеет максимальное значение, равное 6, и минимальный порядковый номер. Она связана с вершинами X1, X3, X8, X9, X12, X15. Посчитаем для этих вершин функционалы:
L(X1)=5-1=4, L(X3)=5-1=4, L(X8)=6-1=5, L(X9)=6-1=5, L(X10)=4-0=4, L(X12)=6-1=5, L(X13)=4-0=4, L(X15)=6-1=5.
Стягиваем вершину X1, X3 с базовой в третий корпус, т.к. они имеют минимальный функционал, равный 4.
Таблица 7
| X8 | X9 | X10 | X12 | X13 | X15 | ||
| X8 | 0 | 1 | 1 | 1 | 1 | 0 | 2 |
| X9 | 1 | 0 | 1 | 1 | 0 | 1 | 2 |
| X10 | 1 | 1 | 0 | 0 | 0 | 1 | 1 |
| X12 | 1 | 1 | 0 | 0 | 1 | 1 | 2 |
| X13 | 1 | 0 | 0 | 1 | 0 | 0 | 2 |
| X15 | 0 | 1 | 1 | 1 | 0 | 0 | 3 |
| 2 | 2 | 1 | 2 | 2 | 3 | 0 |
Так как К155ЛА4 содержит три модуля, элементы X1, X3, X6 помещаем в одну микросхему. Для оставшихся несвязанных элементов будем продолжать компоновку.
Таблица 8
| X8 | X9 | X10 | X12 | X13 | X15 | ||
| X8 | 0 | 1 | 1 | 1 | 1 | 0 | 4 |
| X9 | 1 | 0 | 1 | 1 | 0 | 1 | 4 |
| X10 | 1 | 1 | 0 | 0 | 0 | 1 | 3 |
| X12 | 1 | 1 | 0 | 0 | 1 | 1 | 4 |
| X13 | 1 | 0 | 0 | 1 | 0 | 0 | 2 |
| X15 | 0 | 1 | 1 | 1 | 0 | 0 | 3 |
За базовую принимаем вершину X8, т.к. она имеет максимальное значение, равное 4, и минимальный порядковый номер. Она связана с вершинами X9, X10, X12, X13. Посчитаем для этих вершин функционалы:
L(X9)=4-1=3, L(X10)=3-1=2, L(X12)=4-1=3, L(X13)=2-1=1, L(X15)=3-0=3.
Стягиваем вершину X10, X13 с базовой в четвёртый корпус, т.к. они имеют минимальный функционал.
Таблица 9
| X9 | X12 | X15 | ||
| X9 | 0 | 1 | 1 | 2 |
| X12 | 1 | 0 | 1 | 2 |
| X15 | 1 | 1 | 0 | 1 |
| 2 | 2 | 1 | 0 |
Так как К155ЛА4 содержит три модуля, элементы X8, X10, X13 помещаем в одну микросхему.
Аналогично стягиванием оставшиеся вершины X9, X12, X15 в пятый корпус и помещаем в микросхему.
Выбираем микросхему К155ТВ1. В ней содержится только один модуль, поэтому процесс компоновки проводить не будем, а поместим каждый элемент первого блока в отдельную микросхему.
Компоновка второго блока
Второй блок состоит из пяти логических элементов 2И-НЕ, которые не связаны между собой. Поэтому четыре из них стягиваются в один корпус микросхемы К155ЛА3, а пятый в другой, т.к. микросхема К155ЛА3 содержит только 4 логических элемента.
Компоновка третьего блока
Третий блок состоит из одного JK-триггера, поэтому помещаем его в корпус микросхемы К155ТВ1, содержащей только один элемент.
В результате проведения процесса последовательной компоновки конструктивных узлов РЭА, получили схему электрическую принципиальную состоящую из пяти микросхем D2, D3, D4, D5, D6 типа К155ЛА4, двух микросхем D7, D8 типа К155ЛА3 и одной микросхемы D1 типа К155ТВ1. Схема электрическая принципиальная приведена в приложении 1. Перечень элементов к этой схеме в приложении 2.
По этой схеме построим граф (рис. 4).
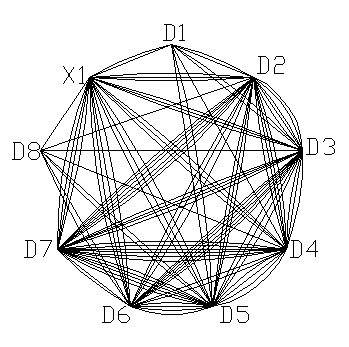
Рис.4
Размещение элементов
Дата: 2019-07-31, просмотров: 212.
