Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

К основным энергетическим характеристикам антенны относят коэффициент усиления и коэффициент направленного действия.

Коэффициент усиления передатчика:

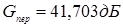
Для того, чтобы выразить G _пер в разах необходимо использовать известное соотношение:

 

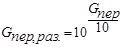 (4.1)

 

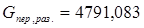
Коэффициент направленного действия (КНД) определяется как отношение коэффициента усиления к КПД (для двузеркальных антенн КПД примем равным 0,8). При этих значениях, КНД определиться как:

 

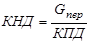; (4.2)

 

КНД=18448,854

 

Расчет радиуса раскрыва большого зеркала

 

В предварительных расчетах радиус раскрыва вычисляется без учета площади затенения. Для определения предварительного радиуса раскрыва (R^/₀) используем следующее соотношение:

 

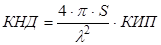 (4.3)

где КИП примем равным 0,6;

 

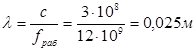 (4.4)

 

Выразим из данного соотношения площадь раскрыва и затем определим R^/₀:

 

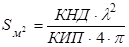 (4.5)

 

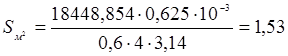
Площадь окружности определяется по формуле:

 

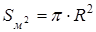 (4.6)

 

В результате получим, что предварительный радиус равен:

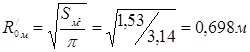
Теперь мы можем получить диаметр как большого, так и малого зеркал:

 

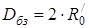 (4.7)

 

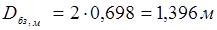
При этом диаметр малого зеркала определяется в соответствии с рекомендациями:

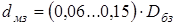
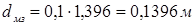
В дальнейшем нам необходимо учитывать площадь затенения, иными словами определить площадь малого зеркала, и соответственно вычислить радиус раскрыва с учетом этой площади. Площадь тени можно определить как:

 

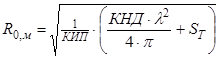, (4.8)

 

где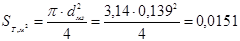

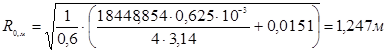
Теперь нам необходимо проверить соотношение R^/₀ < R₀. Анализируя полученные результаты, можно сделать вывод, что условие удовлетворено. Дальнейший расчет основан на выборе угла раскрыва (Ψ₀) и угла облучения (φ₂):

Ψ₀= 100⁰…105⁰, примем Ψ₀=103⁰;

φ₂= 40⁰…41⁰, примем φ₂=41⁰;

 

Расчет эксцентриситета малого зеркала гиперболы, фокусных расстояний зеркал и диаметра облучателя

 

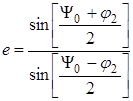; (4.9)

 

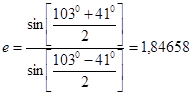
Для дальнейшего расчета нам необходимо определить фокусное расстояние большого (F) и малого (f) зеркал. Это можно сделать, используя следующее соотношение:

 

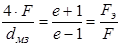; (4.10)

 

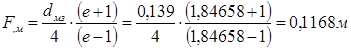
Из приведенного выше соотношения видно, что F _э определится как:

 

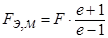; (4.11)

 

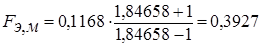
Теперь рассчитаем фокусное расстояние малого зеркала, при этом формула для его определения выглядит следующим образом:

 

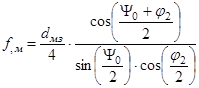; (4.12)

 

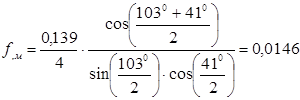
Разность расстояний от фокусов до произвольной точки на поверхности гиперболоида постоянна, т.е. 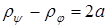, где 2а – это расстояние между его вершинами. Расстояние между фокусами гиперболоида 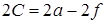. При этом эксцентриситет образующей гиперболы равен .

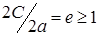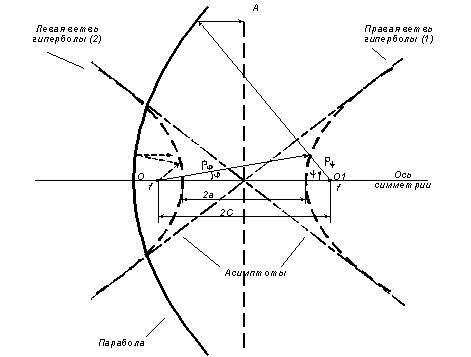
Рисунок 4.2 – графическое представление расстояний 2С и 2а

 

Теперь можно отыскать численные значения расстояний 2С и 2а. Для этого используем выражение:

 

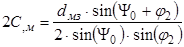; (4.13)

 

;

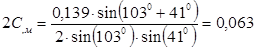
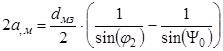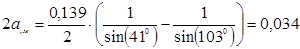
Выполним проверку на условие 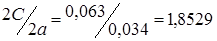, условие  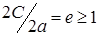удовлетворено, следовательно, расстояния найдены, верно.

Необходимо определить диаметр облучателя:

 

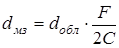; (4.14)

 

Таким образом, диаметр облучателя можно определить как:

;

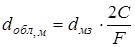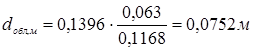
При этом условие 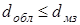выполняется.

 

Расчет питающей линии

 

В качестве облучателя используется конический рупор, питание таких рупоров осуществляется от круглого волновода или через плавный переход от прямоугольного.

Применим круглый волновод с основной волной 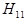. Волновод должен подводить к облучателю только волну  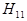и пропускать заданную мощность.

Соотношение радиуса волновода и критической длины волны 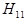 в волноводе:

 

 

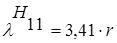
Отсюда r, учитывая, что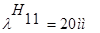

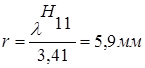
Нижняя граница работы волновода на основной частоте 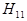 определим:

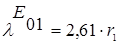
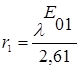=7,7 мм

Таким образом, радиус волновода надлежит выбирать из полученного неравенства:

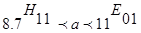
Выбираем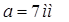

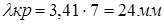
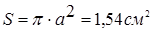
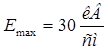 из-за возможных неоднородностей, качества поверхности внутренних стенок волновода, чистоты заполняющего волновод воздуха большее значение 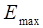брать не рекомендуется.

Определим максимальную мощность, которая может быть передана через волновод:

 

 

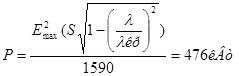
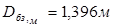
В четвертой главе произведена сравнительная характеристика антенн спутниковой связи. Наиболее актуальной для использования в проекте является двухзеркальная антенна по схеме Кассегрена. Произведен методический расчет:– диаметров большого и малого зеркал: 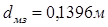– радиуса раскрыва;– фокусных расстояний зеркал и диаметра облучателя;– волноводной линии.

Следует отметить, что на судне приемно-передающая антенна устанавливается на гиростабилизирующую платформу, которая нейтрализует отклонение направления сигнала при качке, за счет специальной конструкции.