Для организации передачи данных по энергосетям передаваемая информация подвергается тем же преобразованиям, что и при передаче данных по телефонной сети общего пользования. То есть передаваемая информация на передающем конце подвергается кодированию, цифро-аналоговому преобразованию и модуляции, а на приемном конце – демодуляции, аналого-цифровому преобразованию и декодированию.
Поскольку каждый абонент системы передачи данных является как источником, так и получателем информации, то на каждом ПК необходимо организовать передающую и приемную части системы. Это удобно организовать, используя для передатчика и приемника один внутренний и внешний интерфейсы. Таким образом, обобщеная структурная схема системы передачи данных на одном ПК будет иметь следующий вид (рис. 3.1).
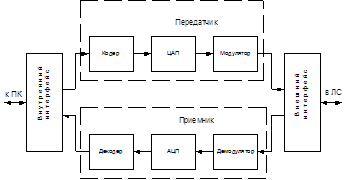
Рисунок 3.1 – Обобщеная схема системы передачи данных
Из рис. 3.1 видно, что передаваемые информация в цифровом виде поступает в устройство передачи данных через внутренний интерфейс. Внутренний интерфейс служит для выделения из всего потока данных, которые передаются по внутренней шине данных ПК, тех, которые предназначены для передачи в линию связи. Процесс выделения происходит в соответствии адресной информацией, передаваемой по шине адреса. Из этого следует, что внутренний интерфейс обеспечивает поступление в передающее устройство только тех данных, которые необходимо передать по линии связи. Таким же образом, принятые приемником данные, передаются через внутренний интерфейс в ПК для дальнейшей обработки.
Внешний интерфейс служит для согласования устройства передачи и приема данных с линией связи. Он выполняет функции разделения сигналов по направлениям, адаптацию сигналов к среде передачи, развязки по напряжению, согласования сопротивлений в линии и линейном тракте и выделения только полезного сигнала.
Процессы кодирования, декодирования, цифро-аналогового и аналого-цифрового преобразования, а так же модуляции и демодуляции выполняются микропроцессорной системой. Эта система имеет в своем составе постоянное запоминающее устройство (ПЗУ), которое содержит программное обеспечение, обеспечивающее выполнение определенных функций микропроцессорной системы. Так же в нее входят оперативное запоминающее устройство (ОЗУ) и перепрограммируемое постоянное запоминающее устройство (ППЗУ). ОЗУ используется для хранения промежуточных результатов вычислений, ключевых данных. В ППЗУ заносятся временные алгоритмы работы микропроцессорной системы. Все преобразования, которым подвергается сигнал, выполняются в самом микропроцессоре (МП). К используемому микропроцессору предъявляются особые требования. Так как при реализации алгоритмов кодирования и декодирования основной математической операцией является умножение с плавающей запятой, то при использовании классических МП резко возрастает сложность написания программ и время их выполнения. Сегодня в цифровой обработке сигналов широко применяются цифровые сигнальные процессоры, называемые еще – DSP-контроллерами. Основное достоинство этих DSP-контроллеров - возможность выполнения однотактных умножений, сложений, наличие специфических команд, таких как двоичная инверсия. Использование такого DSP-контроллера резко снижает требования к его быстродействию, что положительно сказывается на цене системы. Используя в микропроцессорной системе, наряду с обычным микропроцессором, DSP-контроллер, можно перераспределить выполняемые функции. Так МП занимается организацией обмена данными по шине данных с ПК, генерируя и получая адресную информацию по шине адреса, то есть выполняет функции внутреннего интерфейса. Так как быстродействие DSP-контроллера на много выше МП, то он выполняет функции кодирования, декодирования, цифро-аналогового и аналого-цифрового преобразования, а так же модуляции и демодуляции.
Внешний интерфейс организован несколькими устройствами, которые выполняют каждый свою функцию. Для адаптации сигнала к линии связи используется адаптивный эквалайзер. Эхокомпенсатор используется для разделения сигналов по направлениям. Устройство присоединения, выполняющее следующие функции: отсекает промчастоту и пропускает только полезный высокочастотный сигнал, служит заградительным устройством для высокого напряжения, служит согласующим элементом между высокочастотным кабелем и линейным трактом, так как волновое сопротивление кабеля не равно характеристическому сопротивлению линейного тракта.
Таким образом, общая структурная схема системы передачи данных по энергосети имеет следующий вид (рис. 3.2), где, УП – устройство присоединения, ША – шина адреса, ШД – шина данных.
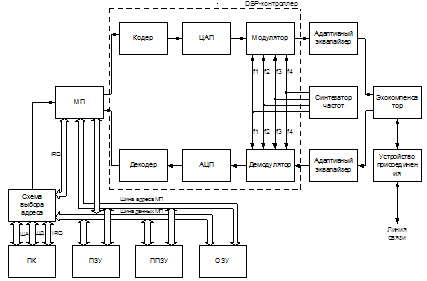
Рисунок 3.2 – Структурная схема системы передачи информации по энергосетям
Исходя из этой схемы, можно привести структурную схему передатчика (рис. 3.3).
Функционирование МП осуществляется по алгоритму, записанному в ПЗУ и ППЗУ. Данные, которые анализируются микропроцессором, заносятся в ОЗУ. После выполнения всех необходимых операций над данными, происходит очистка ОЗУ, для того чтобы принять другие данные. Принцип работы кодера зависит от способа кодирования, который выбирается из условия получения минимальной вероятности ошибки и максимальной помехозащищенности. Модуляция должна обеспечивать перенос спектра полезного сигнала в область частот, где он будет меньше всего подвержен воздействию помех. Так же от способа модуляции зависит скорость передачи данных и максимальная помехоустойчивость. Поэтому от выбора вида модуляции зависят основные параметры системы передачи данных в целом.
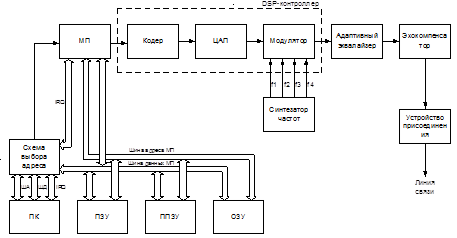
Рисунок 3.3 – Структурная схема передатчика
Поскольку передача данных осуществляется в четырех частотных диапазонах, которые расположены довольно близко друг от друга, то появляется необходимость ограничения спектров передаваемых сигналов в рамках частотного диапазона. Ограничение производится для того, чтобы сигналы, передаваемые в одном диапазоне, не влияли на сигналы, которые передаются в другом частотном диапазоне. Для ограничения спектров используются полосовые фильтры, настроенные каждый на свою резонансную частоту.
Управление процессами, происходящими в микропроцессоре и DSP-контроллере, происходит с помощью драйверов, которые поставляются вместе с микропроцессором и DSP-контроллером от фирмы-производителя.
АНАЛИЗ МЕТОДОВ КОДИРОВАНИЯ
Линейные методы кодирования
Данные пользователя, поступающие от DTE, уже являются цифровыми, представленными в униполярном или биполярном коде без возврата к нулю — NRZ. При передаче данных на большие расстояния в коде NRZ возникают следующие проблемы. С течением времени нарастает постоянный ток, блокируемый некоторыми электрическими устройствами цифрового тракта, например, трансформаторами, что приводит к искажению передаваемых импульсов. Передача длинных серий нулей или единиц приводит к нарушению правильной работы устройств синхронизации. Отсутствует возможность контроля возникающих ошибок на уровне физического канала.
Перечисленные проблемы решаются при помощи линейного кодирования. Параметры получаемого линейного сигнала должны быть согласованы с характеристикой, используемой линии, и отвечать ряду следующих требований. Энергетический спектр линейного сигнала должен быть как можно уже. В нем должна отсутствовать постоянная составляющая, что позволяет повысить верность либо дальность передачи. Структура линейного сигнала должна обеспечивать возможность выделения тактовой частоты на приемной стороне. Необходимо обеспечить возможность постоянного контроля за ошибками на уровне физической линии. Линейный код должен иметь достаточно простую техническую реализацию. Примеры линейных кодов приведены на рис. 4.1 [2].
Формирование требуемого энергетического спектра может быть осуществлено соответствующим изменением структуры импульсной последовательности и выбором нужной формы импульсов
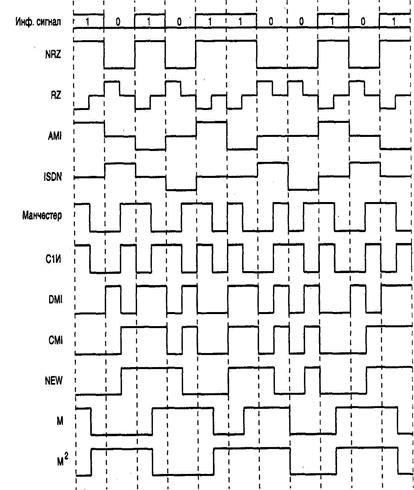
Рисунок 4.1 - Примеры кодирования линейными кодами
Например, даже сокращение длительности импульсов в два раза (биимпульсный код с возвратом к нулю, RZ) вдвое уменьшает уровень постоянной составляющей и увеличивает уровень тактовой составляющей в спектре такого сигнала.
Код Манчестер характеризуется однозначным соответствием последовательности чередования импульсов внутри тактового интервала. А именно, "1" исходного цифрового сигнала передается нулевым импульс в первом полутактовом интервале и единичным — во втором. Для символа "О" принимается обратный порядок чередования импульсов (биимпульс 10).
Относительное кодирование позволяет решить проблему неопределенности фазы биимпульса на приемной стороне.
Сверточные коды
Сверточный код создается прохождением передаваемой информационной последовательности через линейный сдвиговый регистр с конечным числом состояний. В общем виде, регистр сдвига состоит из К (k-битовых) ячеек и линейного преобразователя, состоящего из n функциональных генераторов и выполняющего алгебраические функции. Входные данные к кодеру, которые считаются двоичными, поступают вдоль регистра сдвига по k бит за раз. Число входных бит для каждой k-битовой последовательности равно n. Следовательно, кодовая скорость, определенная как RC=k/n, согласуется с определением скорости блокового кода [18]. Параметр К называется кодовым ограничением сверточного кода. Для пояснения принципа работы кодера рассмотрим сверточный кодер со скоростью кода 1/3, показанный на рис.4.2.
Считается, что первоначально все ячейки регистра сдвига находятся в нулевом состоянии. Допустим, что первый входной бит «1». Он без задержек появляется на выходе первой ячейки регистра и, соответственно, на всех трех входах выходного ключа (мультиплексора). Ключ поочередно выдает содержимое входов, и в результате выходная последовательность из трех бит будет – 111. Допустим, что второй входной бит «0». Он записывается в первую ячейку регистра, вытесняя предыдущий бит («1»), во вторую ячейку – и на входах мультиплексора появляются 001. Если третий входной бит 1, выходная последовательность 100 и т. д. Таким образом, в ответ на каждый входной бит (k=1) сверточный кодер откликается тремя битами, по числу функциональных генераторов (n=3).
Рисунок 4.2 – Сверточный кодер со скоростью кода 1/3
Имеются три альтернативных метода описания сверточного кода: древовидная диаграмма, решетчатая диаграмма и диаграмма состояний. Для приведенного выше кодера древовидная диаграмма показана на рис. 4.3.
Предположим, что кодер находится в нулевом состоянии (все нули). Диаграмма показывает, что, если первый вход 0 – выходная последовательность 000, а если первый вход 1 – выходная последовательность 111. Если в следующий момент первый вход 1, а второй 0, то второй набор выходных бит 001. Далее, если третий входной бит 0, то выходная последовательность 011, если же третий входной бит 1, то на выходе – 100.
Аналогичным способом можно описать более сложный код со скоростью 2/3, а так же недвоичные коды (если число символов в алфавите q³2k, k>1)
Рисунок 4.3 – Древовидная диаграмма для кода со скоростью 1/3
Сверточные коды относятся к помехоустойчивым кодам, поэтому они часто используются после относительных кодов, которые являются накопителями ошибок, а так же сверточное кодирование используется в системах с модуляцией, обладающей низкой помехоустойчивостью. Так, применение многопозиционной QAM в чистом виде сопряжено с проблемой недостаточной помехоустойчивости. Поэтому во всех современных высокоскоростных протоколах QAM используется совместно с решетчатым кодированием — специальным видом сверточного кодирования. В результате появился новый способ модуляции, называемый треллис-модуляцией (ТСМ). Выбранная определенным образом комбинация конкретной QAM помехоустойчивого кода в отечественной технической литературе носит название сигналъно-кодовой конструкции (СКК). СКК позволяют повысить помехозащищенность передачи информации наряду со снижением требований к отношению сигнал/шум в канале на 3—6 дБ. При этом число сигнальных точек увеличивается вдвое за счет добавления к информационным битам одного избыточного, образованного путем сверточного кодирования. Расширенный таким образом блок битов подвергается все той же QAM. В процессе демодуляции производится декодирование принятого сигнала по алгоритму Витерби [11]. Именно этот алгоритм за счет использования введенной избыточности и знания предыстории процесса приема позволяет по критерию максимального правдоподобия выбрать из сигнального пространства наиболее достоверную эталонную точку.
Выбор способов модуляции и кодирования сводится к поиску такого заполнения сигнального пространства, при котором обеспечивается высокая скорость и высокая помехоустойчивость. Комбинирование различных ансамблей многопозиционных сигналов и помехоустойчивых кодов порождает множество вариантов сигнальных конструкций. Согласованные определенным образом варианты, обеспечивающие улучшение энергетической и частотной эффективности, и являются сигнально-кодовыми конструкциями. Задача поиска наилучшей СКК является одной из наиболее сложных задач теории связи. Современные высокоскоростные протоколы модуляции (V.32, V.32bis, V.34 и др.) предполагают обязательное применение сигнально-кодовых конструкций.
Все применяемые сегодня СКК используют сверточное кодирование со скоростью n—1/n, т.е. при передаче одного сигнального элемента используется только один избыточный двоичный символ [2].
Таким образом, в системах с нестабильной помеховой обстановкой для обеспечения высокой помехоустойчивости целесообразно использовать сочетание относительного кодирования и сверточного кодирования, а в случаях применения QAM – треллис-модуляции.
ОБЗОР ВИДОВ МОДУЛЯЦИИ
Преобразование несущего гармонического колебания (одного или нескольких его параметров) в соответствии с законом изменения передаваемой информационной последовательности называется модуляцией. При передаче цифровых сигналов в аналоговом виде оперируют понятием – манипуляция.
Способ модуляции играет основную роль в достижении максимально возможной скорости передачи информации при заданной вероятности ошибочного приема. Предельные возможности системы передачи можно оценить с помощью известной формулы Шеннона, определяющей зависимость пропускной способности С непрерывного канала с белым гауссовским шумом от используемой полосы частот F и отношения мощностей сигнала и шума Pс/Pш .
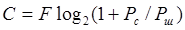, (5.1)
где PС — средняя мощность сигнала;
PШ — средняя мощность шума в полосе частот.
Пропускная способность определяется как верхняя граница реальной скорости передачи информации V. Приведенное выше выражение позволяет найти максимальное значение скорости передачи, которое может быть достигнуто в гауссовском канале с заданными значениями: ширины частотного диапазона, в котором осуществляется передача (DF) и отношения сигнал – шум (PС/РШ).
Вероятность ошибочного приема бита в конкретной системе передачи определяется отношением PС/РШ. Из формулы Шеннона следует, что возрастание удельной скорости передачи V/DF требует увеличения энергетических затрат (РС) на один бит. Зависимость удельной скорости передачи от отношения сигнал/шум показана на рис. 5.1.
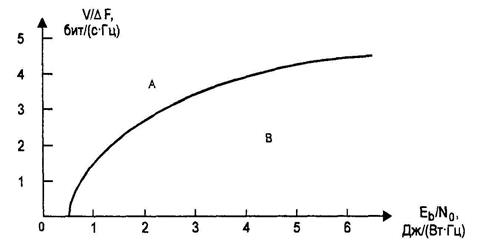
Рисунок 5.1 – Зависимость удельной скорости передачи от отношения сигнал/шум
Любая система передачи может быть описана точкой, лежащей ниже приведенной на рисунке кривой (область В). Эту кривую часто называют границей или пределом Шеннона. Для любой точки в области В можно создать такую систему связи, вероятность ошибочного приема у которой может быть настолько малой, насколько это требуется [2].
Современные системы передачи данных требуют, чтобы вероятность необнаруженной ошибки была не выше величины 10-4…10-7 [11].
В современной цифровой технике связи наиболее распространенными являются частотная модуляция (FSK), относительная фазовая модуляция (DPSK), квадратурная фазовая модуляция (QPSK), фазовая модуляция со сдвигом (смещением), обозначаемая как O-QPSK или SQPSK, квадратурная амплитудная модуляция (QAM).
При частотной модуляции значениям «0» и «1» информационной последовательности соответствуют определенные частоты аналогового сигнала при неизменной амплитуде. Частотная модуляция весьма помехоустойчива, однако при частотной модуляции неэкономно расходуется ресурс полосы частот канала связи. Поэтому этот вид модуляции применяется в низкоскоростных протоколах, позволяющих осуществлять связь по каналам с низким отношением сигнал/шум.
При относительной фазовой модуляции в зависимости от значения информационного элемента изменяется только фаза сигнала при неизменной амплитуде и частоте. Причем каждому информационному биту ставится в соответствие не абсолютное значение фазы, а ее изменение относительно предыдущего значения.
Чаще применяется четырехфазная DPSK, или двукратная DPSK, основанная на передаче четырех сигналов, каждый из которых несет информацию о двух битах (дибите) исходной двоичной последовательности. Обычно используется два набора фаз: в зависимости от значения дибита (00, 01, 10 или 11) фаза сигнала может измениться на 0°, 90°, 180°, 270° или 45°, 135°, 225°, 315° соответственно. При этом, если число кодируемых бит более трех (8 позиций поворота фазы), резко снижается помехоустойчивость DPSK. По этой причине для высокоскоростной передачи данных DPSK не используется.
Модемы с 4-позиционной или квадратурной фазовой модуляцией используются в системах, в которых теоретическая спектральная эффективность устройств передачи BPSK (1 бит/(с·Гц)) недостаточна при имеющейся в наличии полосе частот. Различные методы демодуляции, используемые в системах BPSK, применяются также и в системах QPSK. Кроме прямого распространения методов двоичной модуляции на случай QPSK используется также 4-позиционная модуляция со сдвигом (смещением). Некоторые разновидности QPSK и BPSK приведены в табл. 5.1 [8].
При квадратурной амплитудной модуляции изменяется как фаза, так и амплитуда сигнала, что позволяет увеличить количество кодируемых бит и при этом существенно повысить помехоустойчивость. В настоящее время используются способы модуляции, в которых число кодируемых на одном бодовом интервале информационных бит, может достигать 8…9, а число позиций сигнала в сигнальном пространстве – 256…512.
Таблица 5.1 – Разновидности QPSK и BPSK
| Двоичная PSK | Четырехпозиционная PSK | Краткое описание |
| BPSK | QPSK | Обычные когерентные BPSK и QPSK |
| DEBPSK | DEQPSK | Обычные когерентные BPSK и QPSK с относительным кодированием и СВН |
| DBSK | DQPSK | QPSK с автокорреляционной демодуляцией (нет СВН) |
| FBPSK | FQPSK O-QPSK DEOQPSK FOQPSK р/4-DEQPSK | BPSK или QPSK С запатентованным процессором Феера, пригодным для систем с нелинейным усилением QPSK со сдвигом (смещением) QPSK со сдвигом и относительным кодированием QPSK со сдвигом и запатентованным Феером процессорами QPSK с относительным кодированием и фазовым сдвигом на р/4 |
Квадратурное представление сигналов является удобным и достаточно универсальным средством их описания. Квадратурное представление заключается в выражении колебания линейной комбинацией двух ортогональных составляющих — синусоидальной и косинусоидальной:
S(t)=x(t)sin(wt+(j))+y(t)cos(wt+(j)), (5.2)
где x(t) и y(t) — биполярные дискретные величины.
Такая дискретная модуляция (манипуляция) осуществляется по двум каналам на несущих, сдвинутых на 90° друг относительно друга, т.е. находящихся в квадратуре (отсюда и название представления и метода формирования сигналов).
Поясним работу квадратурной схемы (рис. 5.2) на примере формирования сигналов QPSK.
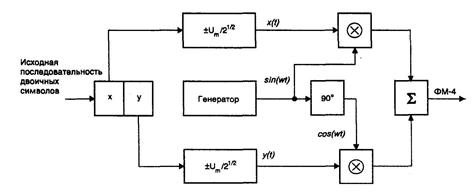
Рисунок 5.2 – Схема квадратурного модулятора
Исходная последовательность двоичных символов длительностью Т при помощи регистра сдвига разделяется на нечетные импульсы Y, которые подаются в квадратурный канал (coswt), и четные — X, поступающие в синфазный канал (sinwt). Обе последовательности импульсов поступают на входы соответствующих формирователей манипулирующих импульсов, на выходах которых образуются последовательности биполярных импульсов x(t) и y(t).
Манипулирующие импульсы имеют амплитуду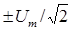 
и длительность 2T. Импульсы x(t) и y(t) поступают на входы канальных перемножителей, на выходах которых формируются двухфазные фазомодулированные колебания. После суммирования они образуют сигнал QPSK.
Для приведенного выше выражения для описания сигнала характерна взаимная независимость многоуровневых манипулирующих импульсов x(t), y(t) в каналах, т.е. единичному уровню в одном канале может соответствовать единичный или нулевой уровень в другом канале. В результате выходной сигнал квадратурной схемы изменяется не только по фазе, но и по амплитуде. Поскольку в каждом канале осуществляется амплитудная манипуляция, этот вид модуляции называют амплитудной квадратурной модуляцией.
Пользуясь геометрической трактовкой, каждый сигнал QAM можно изобразить вектором в сигнальном пространстве.
Отмечая только концы векторов, для сигналов QAM получаем изображение в виде сигнальной точки, координаты которой определяются значениями x(t) и y(t). Совокупность сигнальных точек образует так называемое сигнальное созвездие.
На рис. 5.3 показана структурная схема модулятора, а на рис. 5.4 – сигнальное созвездие для случая, когда x(t) и y(t) принимают значения ±1, ±3 (QAM-4).
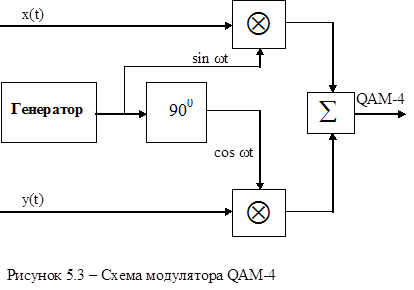
Рисунок 5.4 – Сигнальная диаграмма QAM-4
Величины ±1, ±3 определяют уровни модуляции и имеют относительный характер. Созвездие содержит 16 сигнальных точек, каждая из которых соответствует четырем передаваемым информационным битам.
Комбинация уровней ±1, ±3, ±5 может сформировать созвездие из 36 сигнальных точек. Однако из них в протоколах ITU-T используется только 16 равномерно распределенных в сигнальном пространстве точек.
Существует несколько способов практической реализации QAM-4, наиболее распространенным из которых является так называемый способ модуляции наложением (SPM). В схеме, реализующей данный способ, используются два одинаковых QPSK (рис. 5.5).
Используя эту же методику получения QAM, можно получить схему практической реализации QAM-32 (рис.5.6).
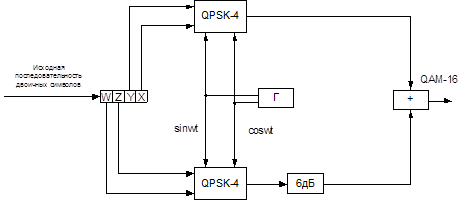
Рисунок 5.5 – Схема модулятора QAM-16
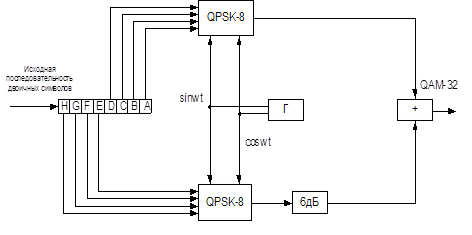
Рисунок 5.6 – Схема модулятора QAM-32
Получение QAM-64, QAM-128 и QAM-256 происходит таким же образом. Схемы получения этих модуляций не приводятся по причине их громоздкости.
Из теории связи известно, что при равном числе точек в сигнальном созвездии спектр помехоустойчивость систем QAM и QPSK различна. При большом числе точек сигналов спектр QAM идентичен спектру сигналов QPSK. Однако сигналы системы QAM имеют лучшие характеристики, чем системы QPSK. Основная причина этого состоит в том, что расстояние между сигнальными точками в системе QPSK меньше расстояния между сигнальными точками в системе QAM.
На рис. 5.7 представлены сигнальные созвездия систем QAM-16 и QPSK-16 при одинаковой мощности сигнала. Расстояние d между соседними точками сигнального созвездия в системе QAM с L уровнями модуляции определяется выражением:
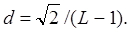(5.3)
Аналогично для QPSK:
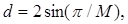(5.4)
где М – число фаз.
Из приведенных выражений следует, что при увеличении значения М и одном и том же уровне мощности системы QAM предпочтительнее систем QPSK. Например, при М=16 (L = 4) dQAM = 0.47 и dQPSK = 0.396, а при М=32 (L = 6) dQAM = 0.28, dQPSK = 0.174 [2].
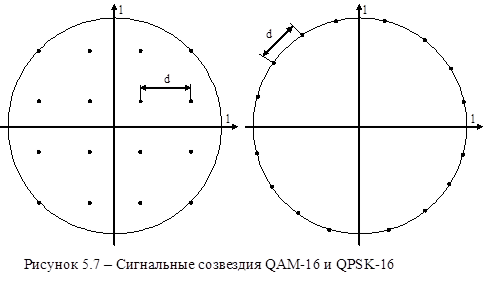
Таким образом, можно сказать, что QAM на много эффективнее по сравнению с QPSK, что позволяет использовать более многоуровневую модуляцию при одинаковом соотношении сигнал/шум. Поэтому можно сделать вывод, что характеристики QAM будут наиболее приближенными к границе Шеннона (рис.5.8) где: 1 – граница Шеннона, 2 – QAM, 3 – М-позиционная АРК, 4 – М-позиционная PSK [8].
Рисунок 5.8 - Зависимость спектральной эффективности различных модуляций от C/N
В общем случае М-позиционные системы QAM с линейным усилением, такие как 16-QAM, 64-QAM, 256-QAM, имеют спектральную эффективность выше, чем у QPSK с линейным усилением, имеющей теоретическую предельную эффективность 2 бит/(с∙Гц).
Одной из характерных особенностей QAM является малые значения внеполосной мощности (рис. 5.9) [8].
Рисунок 5.9 – Энергетический спектр QAM-64
Применение многопозиционной QAM в чистом виде сопряжено с проблемой недостаточной помехоустойчивости. Поэтому во всех современных высокоскоростных протоколах QAM используется совместно с решетчатым кодированием (ТСМ). Сигнальное созвездие ТСМ содержит больше сигнальных точек (позиций сигналов), чем требуется при модуляции без решетчатого кодирования. Например, 16-позиционная QAM преобразует в созвездие 32-QAM с решетчатым кодированием. Дополнительные точки созвездия обеспечивают сигнальную избыточность и могут быть использованы для обнаружения и исправления ошибок. Сверточное кодирование в сочетании с ТСМ вносит зависимость между последовательными сигнальными точками. В результате появился новый способ модуляции, называемый треллис-модуляцией. Выбранная определенным образом комбинация конкретной QAM помехоустойчивого кода носит название сигнально-кодовой конструкции (СКК). СКК позволяют повысить помехозащищенность передачи информации наряду со снижением требований к отношению сигнал/шум в канале на 3 – 6 дБ. В процессе демодуляции производится декодирование принятого сигнала по алгоритму Витерби. Именно этот алгоритм за счет использования введенной избыточности и знания предыстории процесса приема позволяет по критерию максимального правдоподобия выбрать из сигнального пространства наиболее достоверную эталонную точку.
Применение QAM-256 позволяет за 1 бод передавать 8 сигнальных состояний, то есть 8 бит. Это позволяет значительно увеличить скорость передачи данных. Так, при ширине диапазона передачи Df=45 кГц (как в нашем случае) за интервал времени 1/Df можно передать 1 бод, то есть 8 бит. Тогда максимальная скорость передачи по данному частотному диапазону составит
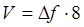, (5.5)
.
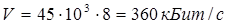Поскольку в данной системе передача производиться по двум частотным диапазонам с одинаковой шириной, то максимальная скорость передачи данной системы составит 720 кбит/с.
Так как передаваемый поток бит содержит не только информационные биты, а и служебные, то информационная скорость будет зависеть от структуры передаваемых кадров. Кадры применяемые в данной системе передачи данных формируются на основе протоколов Ethernet и V.42 и имеют максимальную длину К=1518 бит, из которых КС=64 – служебные. Тогда информационная скорость передачи будет зависеть от соотношения информационных бит и служебных 
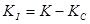, (5.6)
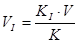, (5.7)
.
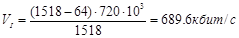Данная скорость превышает скорость, заданную в техническом задании. Поэтому можно сделать вывод, что выбранный способ модуляции удовлетворяет требованиям, поставленным в техническом задании.
Поскольку в данной системе передача осуществляется по двум частотным диапазонам одновременно, то требуется организация двух, параллельно работающих модуляторов. Но следует учитывать, что возможен переход работы системы с основных частотных диапазонов на резервные. Поэтому требуется генерация всех четырех несущих частот и управление ими. Синтезатор частот, предназначенный для генерации несущих частот, состоит из генератора опорного сигнала, делителей и высокодобротных фильтров. В качестве генератора опорных сигналов выступает кварцевый генератор прямоугольных импульсов (рис. 5.10).
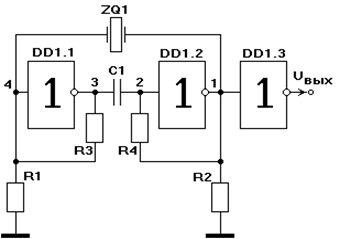
Рисунок 5.10 - Генератор с кварцевой стабилизацией
Делители частоты предназначены для преобразования частоты опорного генератора в несущие частоты путем ее деления. Высокодобротные полосовые фильтры служат для выделения из спектра полученных импульсов необходимую составляющую.
Дата: 2019-07-31, просмотров: 276.
