Для представления графа можно использовать матрицу смежности, матрицу инцидентности либо представить его списком дуг.

Основные способы представления (задания) графов:

1) перечисление множеств V (вершин) и E (ребер), задающих граф. G = (V, E);

2) матричные способы описания;

Пусть G = (V, E), |V| = p, а |E| = q, тогда:

a) матрица смежности – квадратная матрица 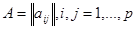, где

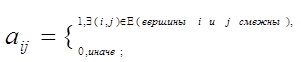
b) матрица инцидентности – прямоугольная матрица .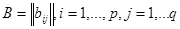

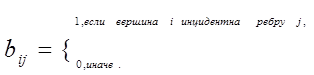
3) список дуг:

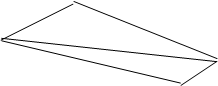
Пример: задан граф G = (V, E), где V = {v1, v2, v3, v4}, E = {v1v2, v2,v3, v1v3, v1v4, v3,v4} = {e1, e2, e3, e4, e5}. Рисунок 3.1.

 v2

 v1

v3

v4

Рисунок 3.1. – Пример построения графа

В данной программе граф представлен списком дуг, в котором каждая вершина содержит информацию о смежном ей ребре, а каждое ребро содержит информацию о тех вершинах, которые ей смежные. Этот способ более экономичен в плане использования памяти.

head: NULL

Рисунок 3.2. – Пример связности ребер графа

Операции над графами

При связанном хранении каждая вершина графа представляет собой структуру graf, состоящую из двух элементов: v1,v2 - предназначены для хранения вершин графа, next - для указателя на структуру, содержащую следующую вершину графа. На первые элементы графа указывает указатель head. Для всех операций над графом используется описание:

typedef struct graf

{ int v1,v2;

struct graf* next;

} Graf;

Graf *g, *head, *temp;

Для реализации операций могут использоваться следующие фрагменты программ:

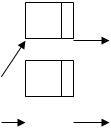
1) определить первый элемент в линейном списке (рисунок 3.1):

printf("v1=");

scanf("%d",&head->v1);

head->next=0;

 NULL

 head NULL

Рисунок 3.3– Создание первого элемента в графе

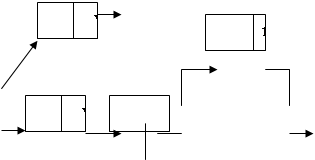
2) вставить дополнительный элемент после указанного узла (рисунок 3.2):

printf("v=");

scanf("%d",&g->v1);

g->next=head;

head=g;

 …. .

 head NULL

Рисунок 3.4– Вставка дополнительного элемента

3) печать всех элементов списка:

printf("Ребра графа: \n");

g=head;

i=0;

while(g! =NULL) {

i++;

printf("РЕБРО%d: v1=%d v2=%d\n", i,g->v1,g->v2);

g=g->next; }

4) удаление ребра:

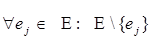
Удалить ребро означает разрушить связь между вершинами, которые являются для данного графа концевыми.

5) удаление вершины:

if((head->v1==i) ||(head->v2==i))

head=head->next;

else{

temp=head;

g=head->next;

while(g) {

if((g->v1==i) ||(g->v2==i)) {

temp->next=g->next;

free(g);

break; }

temp=g;

g=g->next; }}

Удалить вершину означает разрушить связь со смежными ей вершинами и создать новую связь уже без этой вершины. Схема удаления вершины графа, следующей за узлом, на который указывает р находится на рисунке 3.3.

Рисунок 3.5– Схема удаления вершины графа