Воздушные линии 35 и 110 кВ выполняются неизолированным проводом марки А, АС или самонесущими изолированными воздушными проводами (СИП).
Выбираем провод марки АС.
Производим выбор сечения провода по четырем условиям:
1) По длительно-допустимому нагреву максимальным расчётным током:
 |
Производим расчет тока, в А:
 |
 |
По таблицам ПУЭ из условия, что Iдл.доп. Iр.max находим сечение провода: S = 10 мм2 при I дл.доп .= 84 A
2) По экономической плотности тока, в мм2:
 |  |
где Iр.нор – ток в линии при нормальном режиме, в А
(в нашем случае: Iр.нор = Ip.max/2 Iр.нор = 37 А)
γЭК - экономическая плотность тока, в А/мм2, определяется по справочным таблицам в зависимости от типа проводника и числа часов использования максимальной активной нагрузки в год (Тм) [2]
Тм приводится в литературе [5,C.80]
При Тм = 3000 час/год γЭК = 2,5 А/ мм2
2-х сменная работа
Рассчитываем сечение:
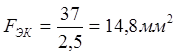
Увеличиваем сечение до 16 мм2
3) Проверяем сечение кабельной линии по условию допустимой потери напряжения:
Допустимые потери в линии согласно ПУЭ не должны превышать (ΔUдоп ) 5% , т.е. должно выполняться условие ΔUдоп ≥ ΔUрасч.
Расчетное значение потери напряжения в линии определяем по формуле, в В:
 | |
где Р р.цеха – активная максимальная расчетная нагрузка, в кВ;
Qр.цеха - реактивная максимальная расчетная нагрузка, в кВАР;
Uср ном – среднее номинальное напряжение в линии, в кВ;
R = ro · L – активное сопротивление в линии, в Ом
X = xo · L – индуктивное сопротивление в линии, в Ом
L -длина линии (расстояние от ГПП до районной ПС), в км (указана в задании), L = 4 км
r0 и х0 - - удельные активные и реактивные сопротивления провода марки АС из литературы [7, С. 40, Т. 2.65]
Из таблиц находим: r0 = 2,06 Ом/км, х0 = 0,43 Ом/км.
Рассчитаем активные и реактивные сопротивления лини:
R = ro · L=2,06 * 4 = 8,24
X = xo · L=0,43 * 4 = 1,72
Потеря напряжения в линии в В:
 |
Потеря напряжения в линии в %:
Оставляем сечение 16 мм2
 |
4) Допустимые потери на «корону», проверяются только для ВЛ 110кВ и выше, но практикой эксплуатации установлено и техническим расчетами подтверждено, что потери на корону не превышают допустимых значений, если сечение проводов не более 70 мм2.
В нашем случае напряжение воздушной линии 75 кВ и расчет потерь на «корону» не производим.
Расчет сборных шин ГПП
Сборные шины распределительных устройств, выбирают в зависимости от конструктивного исполнения, способа присоединения коммутационных аппаратов, ячеек КСО или КРУ и т.д.
В основном сборные шины выполняются из алюминиевых сплавов прямоугольного сечения, одно или многополюсными, или коробчатого сечения.
Выбираем материал шин – алюминий.
Расчет сборных шин РУ 10 кВ производим в следующем порядке:
1) Выбираем сечение шины из условий длительно допустимого нагрева максимально расчетным током.
Рассчитываем максимальный ток, в А:
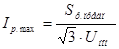(6.13)
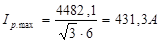
Из условия: Iдл.доп ≥ Iрmax из ПУЭ выбираем шины прямоугольного сечения:
S= 40Ч4 ммІ, Iдл.доп = 480 А
2) Проверяем сечение шин на термическую стойкость при сквозных коротких замыканиях, в мм2:
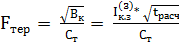(6.14)
Рассчитываем тепловой импульс при токах КЗ, в кА2·с
Вк =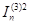 
·tприв , (6.15)
где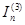 
- ток трехфазного КЗ в точке К1, в кА;
tприв – расчетное время термической стойкости, в с, которое больше расчетного времени кабельной линии на 0,5 с ( на ступень выше по сравнению с расчетом кабельной линии по условию селективности), т.е.
tпривед =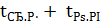 
(6.16)
Ст – термический коэффициент, учитывающий разницу нагрева в условиях нормального режима и в условиях КЗ с учетом допустимой температуры и материала проводника, выбираем из литературы [3, С.190], СТ = 95 Ас2/мм2
Рассчитываем: tпривед =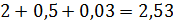 
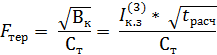
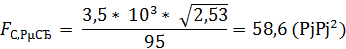
Оставляем сечение 160 мм2
4) Для проверки электродинамической стойкости жестких шин выполним механический расчет [5].
Установлено, что механический резонанс не возникает, если частота собственных колебаний шинных конструкций меньше 30 Гц или больше 200 Гц.
Для алюминиевых шин частота собственных колебаний, в Гц
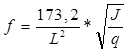(6.17)
где L- расстояние между изоляторами (длина пролета), м;
J - момент инерции поперечного сечения шины относительно оси перпендикулярно направлению изгибающей силы, см4;
q - площадь поперечного сечения шины, см2.
Определим расчетную длину пролета L, т.е. расстояние между точками крепления вдоль шины.
Если принять f о ≥200 Гц, то
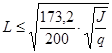(6.18)
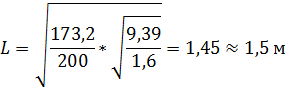
Расположим шины на изоляторах на ребро.
Момент инерции [5, C], в см4
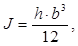
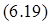
где h – ширина шины, в см;
b – толщина шины, в см.
Площадь поперечного сечения шины, в см2:
q = h · b (6.20)
Рассчитываем момент инерции:
 |
Проверяем шину на электродинамическую стойкость как статическую систему с нагрузкой равной наибольшей электродинамической силе.
Наибольшее удельное усилие, в Н/м
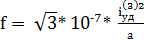(6.21)
где Iуд – ударный ток при КЗ на шинах в точке К2, в А;
а – расстояние между осями крепления, в м;
а = 130 + b (6.22)
130 – минимально допустимое расстояние в свету между токоведущими частями для РУ 10 кВ по ПУЭ, в мм.
а = 160 +40 = 200 мм ≈ 0.2 м
Рассчитываем наибольшее удельное усилие
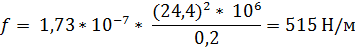
Изгибающий момент, создаваемый распределенной силой в пределах одного пролета, в Н·м:
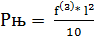(6.23)
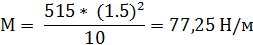
где L – длина пролета, м.
Расчетное напряжение в материале шины, в МПа:
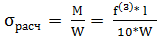(6.24)
где W – момент сопротивления поперечного сечения оси, перпендикулярной направлению изгиба, в см3.
Момент сопротивления шины, расположенной на ребро, в см3:
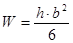(6.24)
Рассчитываем момент сопротивления шины
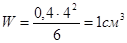
и напряжение в материале шины:
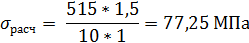
Шины считаются прочными, если расчетное напряжение меньше допустимого:
σдоп ≥ σрасч (6.25)
Допустимые напряжения в литературе [5].
Выбираем марку материала шины: алюминиевый сплав АД31Т1 с допустимым напряжением 200 МПа и σдоп = 90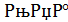 
.
Дата: 2019-07-30, просмотров: 261.
