2.1.1. Построение развернутой индикаторной диаграммы в координатах р-α.
Перестройку индикаторной диаграммы из p-V в развернутую диаграмму удельных давлений (в координатах р-α), действующих на поршень, проще выполнить графическим методом Брикса. Метод Брикса заключается в том, что на длине хода поршня построенной индикаторной диаграммы в координатах p-V описывают полуокружность с центром в точке О.
Для учета влияния длины шатуна откладывают от центра полуокружности (точки О) по направлению нижней мертвой точки бицентровую поправку Брикса в масштабе диаграммы:
a= ход поршня (мм)(по заданию) / ход поршня(мм) (по индикаторной диаграмме)=70/176=0,398
Тогда:
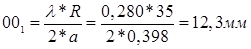 ,
,
где  - радиус кривошипа;
- радиус кривошипа;
 - отношение радиуса кривошипа к длине шатуна.
- отношение радиуса кривошипа к длине шатуна.
Из точки O1 проводим ряд лучей под углами  до пересечения с полуокружностью. Проекции концов этих лучей на линии процесса всасывания, сжатия, расширения и выпуска указывают, какие точки рабочего процесса соответствуют тем или иным углам поворота коленчатого вала.
до пересечения с полуокружностью. Проекции концов этих лучей на линии процесса всасывания, сжатия, расширения и выпуска указывают, какие точки рабочего процесса соответствуют тем или иным углам поворота коленчатого вала.
2.1.2. Рассчитываем избыточное давление газов над поршнем:
 ,
,
при α=370° 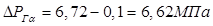
2.1.3. Определяем удельное значение силы инерции от возвратно-поступательного движения масс поршневой группы:
 ,
,
при α=370° 
Здесь 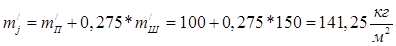 , где конструктивные массы:
, где конструктивные массы:
- поршневой группы 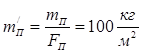 ( поршень из алюминиевого сплава),
( поршень из алюминиевого сплава),
- шатуна  ,
,
- неуравновешенные части одного колена вала без противовесов 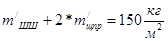 (чугунный литой вал с полыми шейками).
(чугунный литой вал с полыми шейками).
2.1.4. Рассчитываем удельную суммарную силу, действующую вдоль оси цилиндра: 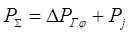 ,
,
при α=370° 
2.1.5. Рассчитываем удельную суммарную силу, действующую на стенку цилиндра:  ,
,
при α=370° 
2.1.6. Рассчитываем удельную суммарную силу, действующую вдоль шатуна:
 ,
,
при α=370° 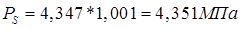
2.1.7. Определяем удельную силу, действующую вдоль кривошипа:
 ,
,
при α=370° 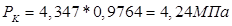
2.1.8. Рассчитываем удельную суммарную силу, действующую по касательной к кривошипу: 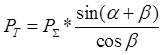 ,
,
при α=370° 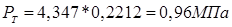
2.1.9. Определяем крутящий момент от одного цилиндра:  ,
,
где 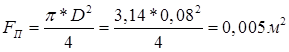 - площадь цилиндра,
- площадь цилиндра,
при α=30° 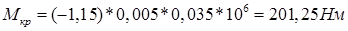
Результаты расчета суммарного крутящего момента (порядок работы цилиндров 1342)
| α, град | Цилиндры |
Нм | |||||||
| 1 | 2 | 3 | 4 | ||||||
| α° | М, Нм | α° | М, Нм | α° | М, Нм | α° | М, Нм | ||
| 0 | 0 | 0 | 540 | 0 | 180 | 0 | 360 | 0 | 0 |
| 30 | 30 | -201,25 | 570 | -91 | 210 | -85,75 | 390 | 320,3 | -57,75 |
| 60 | 60 | -117,3 | 600 | -159 | 240 | -154 | 420 | 126 | -304,5 |
| 90 | 90 | 85,75 | 630 | -99,75 | 270 | -106,8 | 450 | 211,75 | 91 |
| 120 | 120 | 148,75 | 660 | 103,25 | 300 | 68,25 | 480 | 206,5 | 526,75 |
| 150 | 150 | 85,75 | 690 | 192,5 | 330 | 119 | 510 | 112 | 509,25 |
| 180 | 180 | 0 | 720 | 0 | 360 | 0 | 540 | 0 | 0 |
2.1.10. Определяем средний индикаторный момент :
2.1.11. Рассчитываем удельную центробежную силу инерции от вращающейся массы шатуна, сосредоточенной на радиусе кривошипа:
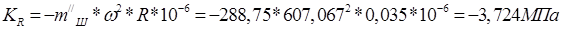 ,
,
где 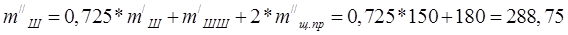
2.1.12. Рассчитываем силу, действующую на поверхность шатунной шейки:
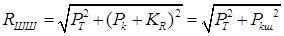
при α=370 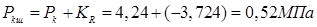 ,
, 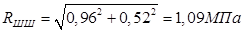
2.2. Построение полярной диаграммы сил, действующей на шатунную шейку 
2.3.1. Строим координатную систему 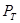 и
и 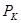 с центром в точке 0, в которой отрицательная ось
с центром в точке 0, в которой отрицательная ось 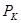 направлена вверх.
направлена вверх.
2.3.2. В таблице результатов динамического расчёта каждому значению α=0, 30°, 60°…70° соответствует точка с координатами 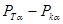 . Наносим на плоскость
. Наносим на плоскость 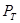 и
и 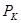 эти точки. Последовательно соединяя точки, получим полярную диаграмму. Вектор. соединяющий центр 0 с любой точкой диаграммы, указывает направление вектора
эти точки. Последовательно соединяя точки, получим полярную диаграмму. Вектор. соединяющий центр 0 с любой точкой диаграммы, указывает направление вектора 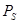 и его величину в соответствующем масштабе.
и его величину в соответствующем масштабе.
2.3.3. Строим новый центр 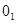 отстоящий от 0 по оси
отстоящий от 0 по оси 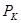 на величину удельной центробежной силы от вращающейся массы нижней части шатуна
на величину удельной центробежной силы от вращающейся массы нижней части шатуна  . В этом центре условно располагают шатунную шейку с диаметром
. В этом центре условно располагают шатунную шейку с диаметром  .
.
2.3.4. Вектор, соединяющий центр 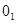 с любой точкой построенной диаграммы, указывает направление действия силы
с любой точкой построенной диаграммы, указывает направление действия силы 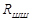 на поверхность шатунной шейки и ее величину в соответствующем масштабе.
на поверхность шатунной шейки и ее величину в соответствующем масштабе.
2.3.5. Касательные линии из центра 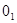 к верхней и нижней частям полярной диаграммы отсекают наиболее нагруженную от наименее нагруженной части поверхности шатунной шейки.
к верхней и нижней частям полярной диаграммы отсекают наиболее нагруженную от наименее нагруженной части поверхности шатунной шейки.
2.3.6. Масляное отверстие располагают в середине наименее нагруженной части поверхности шатунной шейки, для чего восстанавливают перпендикуляр к хорде, соединяющей точки пересечения касательных к верхней и нижней частям полярной диаграммы.
Дата: 2019-07-30, просмотров: 399.
 ,
,