Ребристая структура представляет собой периодически чередующиеся канавки шириной 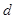 и глубиной
и глубиной 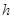 с ребрами толщиной
с ребрами толщиной 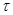 .(Рис .4 .)
.(Рис .4 .)
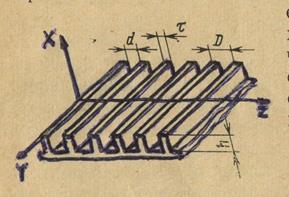
рис.4.
Из выражения:
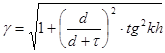 , где (1)
, где (1)
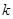 -
- 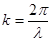
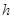 должен быть
должен быть 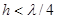 , поэтому возьмем
, поэтому возьмем 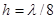 =0,0044м.
=0,0044м.
выразим отсюда отношение 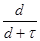 , где
, где 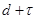 =D:
=D:
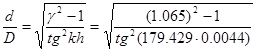 =0,36
=0,36
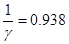
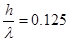
Из графика (рис.5.) находим что 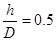 отсюда
отсюда 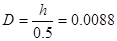 м. следовательно
м. следовательно
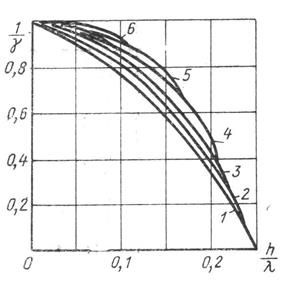
рис.5.
Зависимость замедления 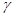 от глубины канавки ребристой структуры
от глубины канавки ребристой структуры 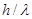 при различных значениях
при различных значениях 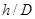 :
:
1) 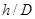 =
= 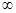 2)
2) 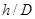 =4 3)
=4 3) 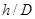 =2
=2
4) 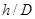 =1,5 5)
=1,5 5) 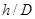 =0,5 6)
=0,5 6) 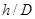 =0,2
=0,2
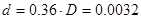 м.
м.
Выразив из выражения (1) 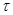 получим:
получим:
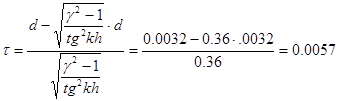 м.
м.
3.Расчет возбуждающего устройства:
В качестве возбуждающего устройства возьмем наиболее широко используемый – раскрыв рупора.
Выбор геометрических размеров рупора и волноводного излучателя:
Выбор размеров поперечного сечения прямоугольного волновода a и b производится из условия распространения в волноводе только основного типа волны 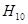 и длине волны.
и длине волны.
В нашем случае подойдет со следующими параметрами:
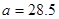 мм
мм 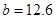 мм (при выборе руководствуемся длиной волны
мм (при выборе руководствуемся длиной волны 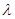 )
)
Длину отрезка волновода 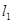 от возбуждающего штыря до закорачивающей стенки выбирается из условия согласования с питающим коаксиалом:
от возбуждающего штыря до закорачивающей стенки выбирается из условия согласования с питающим коаксиалом:
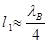 , где (2)
, где (2)
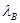 - длина волны в волноводе
- длина волны в волноводе
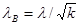

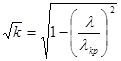
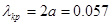 м.
м.
подставив все это в выражение (2) получим:
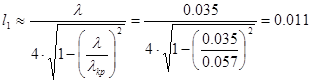 м.
м.
Длина волновода 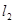 от возбуждающего устройства до горловины рупора выбирается из условия фильтрации высших типов волн и вычисляется по следующей формуле:
от возбуждающего устройства до горловины рупора выбирается из условия фильтрации высших типов волн и вычисляется по следующей формуле:
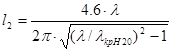 , где
, где
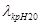 =
= 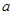 - критическая длина волны
- критическая длина волны 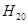 .
.
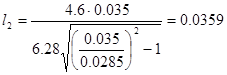 м.
м.
Условие согласования: 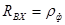
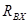 - активная составляющая входного сопротивления штыря
- активная составляющая входного сопротивления штыря
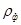 - волновое сопротивление фидера
- волновое сопротивление фидера
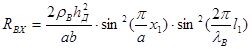 , где (3)
, где (3)
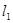 =
= 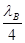 =0,011м.
=0,011м.
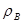 - волновое сопротивление волновода
- волновое сопротивление волновода
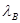 - длина волны в волноводе
- длина волны в волноводе
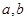 - размеры поперечного сечения волновода
- размеры поперечного сечения волновода
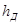 - действующая высота штыря
- действующая высота штыря
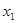 - положение штыря на широкой стенки волновода (
- положение штыря на широкой стенки волновода ( 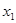
 =0,0143м.)
=0,0143м.)
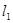 - расстояние от штыря до заворачивающей стенки волновода
- расстояние от штыря до заворачивающей стенки волновода
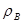 =
= 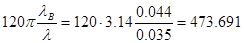 Ом.
Ом.
Действующая высота штыря в волноводе 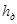 можно определить исходя из условия:
можно определить исходя из условия:
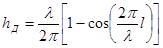 (4)
(4)
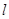 - геометрическая высота штыря
- геометрическая высота штыря
Задаваясь величинами 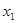 и
и 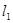 можно по формулам (3) и (4) найти высоту штыря
можно по формулам (3) и (4) найти высоту штыря 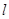 ,при которой получается требуемое
,при которой получается требуемое 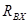 (
( 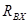 =50 Ом.)
=50 Ом.)
из формулы найдем 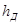 :
:
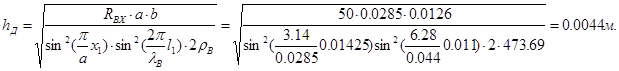
зная значение 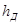 теперь можно найти высоту штыря
теперь можно найти высоту штыря 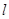 выразив ее из формулы :
выразив ее из формулы :
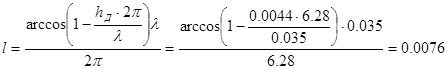 м.
м.
Выбор размеров рупора
Размеры раскрыва пирамидального или секториального рупора 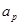 и
и 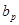 выбираются по требуемой ширине диаграммы направленности в соответствующей плоскости.
выбираются по требуемой ширине диаграммы направленности в соответствующей плоскости.
в плоскости вектора Е:
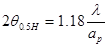 =
=
отсюда выражаем 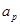 :
:
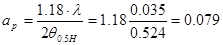 м.
м.
в плоскости вектора Н:
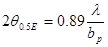
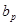 соответственно равняется:
соответственно равняется:
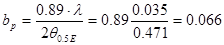 м.
м.
по найденным 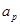 и
и 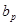 наедем
наедем 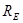 и
и 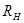 - расстояние от раскрыва до точки, в которой сходятся ребра пирамидального рупора в плоскостях Е и Н соответственно.
- расстояние от раскрыва до точки, в которой сходятся ребра пирамидального рупора в плоскостях Е и Н соответственно.

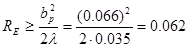 м.
м.
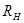 должно удовлетворять условию:
должно удовлетворять условию:
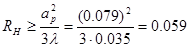 м.
м.
Из треугольников в плоскостях Е и Н следует:
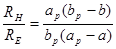
Выразив отсюда  получим:
получим:
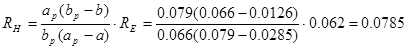 м.
м.
Дата: 2019-07-30, просмотров: 392.