Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Преобразуем схему (рис.1.0) в эквивалентную (рис.1.1):

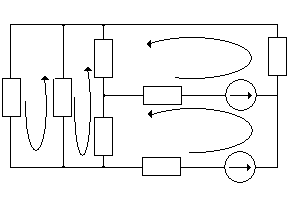
IK3   IK2

IK4                                   R2 R5 E2,r02              R7

R1                     R4

 

IK1

R3     R6

E1,r01

 

Рис.1.1

 

Составляем уравнения для 4-х. контуров:

I-й. Контур:

E2-E1=IK1(R6+r02+r01+R5+R3) +IK2(R5+r01) - IK3R3;

II-й. Контур:

E1= IK2(R5+r01+R7+R2) +IK3R2-IK1(R5+r01);

III-й. Контур:

0=IK3(R4+R3+R2) - IK2R2-IK1R3-IK4R4;

IV-й. Контур:

0=IK4(R1+R4) - IK3R4;

Решаем систему:

10=121IK1-46IK2-22IK2;

30=128IK2-27IK3-46IK1;

0=82IK3-27IK2-22IK1-33IK4;

0=49IK4-33IK3;

 

49IK4-33IK3 => 49IK4=33IK3 => IK4=0,67347IK3;

0=59,77549IK3-27IK2-22IK1;

10=121IK1-46IK2-22IK2;

30=128IK2-27IK3-46IK1;

0=59,77549IK3-27IK2-22IK1;

 

IK1=(128IK2-27IK3-30) /46;

10=121((128IK2-27IK3-30) /46) - 46IK2-22IK3 =>

IK2=(93,02174IK3+88,91304) /290,69566;

IK1=(13,95962IK3+9,15046) /46;

0=59,77549IK3-8,63992IK3-8,3583-6,67634IK3-4,37631

12,63461=44,45923IK3 =>

IK3=0,28418 A;

IK4=0, 19139 A;

IK2=0,39680 A;

IK1=0,28516 A;

Вычисляем истинные токи ветвей электрической цепи, выполняя алгебраическое сложение контурных токов, учитывая их направление:

I1=IK4=0, 19139 A.

I2=IK2-IK3=0,11262 A.

I3=IK1-IK3=0,00098 A.

I4=IK3-IK4=0,09279 A.

I5=IK2-IK1=0,11164 A.

I6=IK1=0,28516 A.

I7=IK2= 0,39680 A.

 

Определение токов во всех ветвях схемы на основе метода наложения

 

a) Нахождение частных токов при исключении источника питания Е2:

Преобразовываем схему (рис.1.0) в эквивалентные схемы на (рис.1.2), (рис.1.3) и (рис.1.4) без Е2, оставив лишь его внутреннее сопротивление r02:

                                 

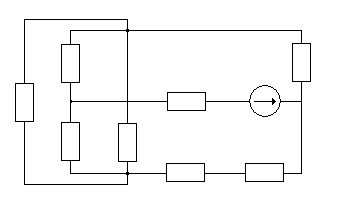
                                    R2                                                 R7          I/7       

                                                    I/2            I/5        E1,r01      

                                                                R5       

                             R1     I/1                                                               

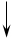                                                     R4                   

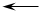                                       R3     I/3       I/4                      I/6

                                                                  R6      r02

Рис.1.2

                                            R2             R7                   

                                          

                                       R5                          

                                                                               R14

                                                               R3             R602

                                  

                                                                                   E1, r01

                                                                                 

Рис.1.3

 

R₁₄=(R₁R₄)/(R₁+R₄)=(16*33)/(16+33)=10,77551 Om;

R₆₀₂=R₆+r₀₂=51+2=53 Om;

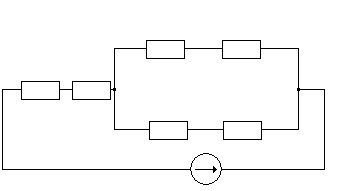
                                                                  R214        R7

                                                                                                    

                                      R5  R23

                                  

                                                                   R314      R602

                                                              

                                                                                      

                           

                                                                            E1,r01                  

Рис.1.4

R214=(R2R14) /(R2+R3+R14) =(27*10.7755) /(27+10.7755+22) =4,86719 Om;

R23=(R2R3) /(R2+R3+R14) =(27*22) /(27+22+10.7755) =9,93718 Om;

R314=(R3R14) /(R3+R14+R2) =(22*10.7755) /(22+10.7755+27) =3,96586 Om;

R2147=R214+R7= 4.8672+55=59,86719 Om;

R314602=R314+R602= 3.9659+53=56,96586 Om;

RЭКВ. =R5+R23+(R2147R314602) /(R2147+R314602) +r1= =43+9.9372+(59.8672*56.9659) /(59.8672+56.9659) +3=85,12743 Om;

I/=E1/RЭКВ. = 30/85.1275=0,35241 A.

I/5=I/=0,35241 A.

I/7=I/(R314+R602) /(R214+R7+R314+R602) = =0.35241*(3.96586+53) /(4.86719+55+3.96586+53) =0,17182 A.;

I/602=I/6=I/(R214+R7) /(R214+R7+R314+R602) = =0.35241*(9.93718+55) /(9.93718+55+3.96586+53) =0,18058 A.;

По II закону Кирхгофа находим частный ток (I/14):

I/14R14-I/602R602+I/7R7=0;

I/14=(I/602R602-I/7R7) /R14= (0.18058*53-0.17182*55) /10.77551=0,0111 A.;

U14=I/14R14= 0.0111*10.77551=0,11961 B.;

I/1=U14/R1= 0,11961/16=0,00748 A.;

I/4=U14/R4= 0.11961/33=0,00362 A.;

I/2=I/7-I/14= 0,17182-0,0111=0,16072 A.;

I/3=I/1+I/4+I/6= 0,00748+0,00362+0,18058=0, 19168 A.;

b) Нахождение частных токов при исключении источника питания Е1:

Преобразуем схему (рис.1.0) в эквивалентные схемы на (рис.1.5), (рис.1.6) и (рис.1.7) без Е1, оставив лишь его внутреннее сопротивление r01:

 

                                                    

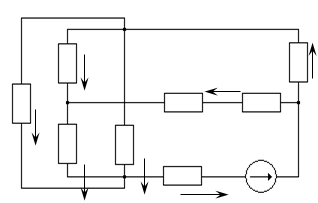
                                     R₂                  

                                                                    

                                                                   I^//₅              R₇           I^//₇

                                                                      R₅         r₀₁

                          R₁    I^//₁                      

                                                                                 

                                             R₃   I^//₃      I^//₄ I^//₆            

                                                  R₄                           

                                                                    R₆         E₂,r₀₂

Рис.1.5

 

                                                                             

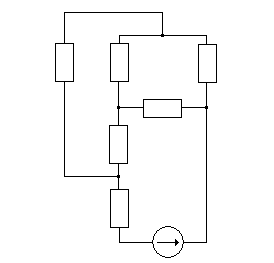
                                          R₁₄     R₂            R₇

             

                                                                        

                                                                    R₅₀₁

                                                        R₃

 

                                                         R₆           E₂,r₀₂

 

Рис.1.6

 

R₁₄=(R₁R₄)/(R₁+R₄)=(16*33)/(16+33)=10,7755 Om;

R₅₀₁=R₅+r₀₁=43+3=46 Om;

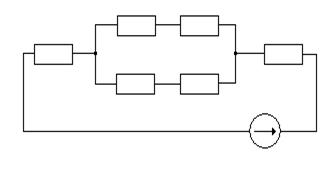                                                      R₁₄      R₂₇

 

                                                

                                                              R₃     R₂₅₀₁

                                          R₆                                      R₇₅₁

 

                                                                    E₂,r₀₂

Рис.1.7

 

R27=(R2R7)/(R2+R7+R501)=(27*55)/(27+55+46)=11,60156 Om;

R2501=(R2R501)/(R2+R7+R501)=(27*46)/(27+55+46)=9,70313 Om;

R7501=(R7R501)/(R2+R7+R501)=(55*46)/(27+55+46)=19,76563 Om;

R1427=R14+R27=10,7755+11,60156=22,37707 Om;

R32501=R3+R2501=22+9,70313=31,70313 Om;

RЭКВ=R6+R7501+(R1427R32501)/(R1427+R32501)+r02=51+19,76563+(22,37707*31,70313)/

/(22,37707+31,70313)+2=85,8836 Om;

I//=E2/RЭКВ=40/85,8836=0,46575 A.;

I//6=I//=0,46575 A.;

I//14=I//((R3+R2501)/(R14+R27+R3+R2501))=0,46575*((22+9,70313)/ /(10,7755+11,60156+22+9,70313))= 0,27303 A.;

I//3=I//*((R14+R27)/(R14+R27+R3+R2501))=0,46575*((10,7755+11,60156)/ /(10,7755+11,60156+22+9,70313))=0.19272 A.;

U14=I//14*R14=0,27303*10,77551=2,94204 B.;

I//1=U14/R1=2,94204/16=0,18388 A.;

I//4=U14/R4=2,94204/33=0,08915 A.;

По II закону Кирхгофа находим частный ток (I // 5):

E2=I // 6(R6+r02) +I // 5(R5+r01) +I // 3R3;

I // 5=(E2-I // 6(R6+r02) - I // 3R3) /(R5+r01) =(40-0,46575*(51+2) - 0, 19272*22) /(43*3) =

=0,24077 A.;

По I закону Кирхгофа находим частный ток (I // 7 и I // 2):

I // 7=I // 6-I // 5=0,46575-0,24077=0,22498 A.;

I // 2=I // 7-I // 1-I // 4=0,22498-0,18388-0,08915=-0,04805 A.;

Вычисляем токи, текущие в ветвях электрической цепи, выполняя алгебраическое сложение частных токов, учитывая их направление:

I1=I/1+I // 1=0,00748 +0,18388 =0,2151 A.;

I2=I/2-I // 2=0,16072-0,04805=0,11267 A.;

I3=I/3-I // 3=0, 19168-0, 19272=-0,00104 A.;

I4=I/4+I // 4=0,00362+0,08915=0,09277 A.;

I5=I/5-I // 5=0,3524-0,24077=0,11163 A.;

I6=I // 6-I/6=0,46575-0,1877=0,27805 A.;

I7=I/7+I // 7=0,1718+0,22498=0,39678 A.;

Составляем баланс мощностей для заданной схемы

 

E1I5+E2I6=I21R1+I22R2+I23R3+I24R4+I25(R5+r01) +I26(R6+r02) +I27R7;

3,88263+10,6064=1,124957+0, 20347+0,03994+0,059915+0,77049+3,726420+8,563179;

14,48903 Вт≈14,48837 Вт;

Представление результатов расчетов в виде таблицы и их сравнение

 

I	Метод контурных токов	Метод наложения	Погрешность
I1	0, 19139	0, 19136	0,003%
I2	0,11262	0,11267	-0,005%
I3	0,00098	0,00104	-0,006%
I4	0,09279	0,09277	0,002%
I5	0,11164	0,11164	0%
I6	0,28516	0,28517	-0,001%
I7	0,39680	0,3968	0%

 

Определение тока во второй ветви методом эквивалентного генератора

 

Удаляем резистор R2 и находим интересующие нас токи электрической цепи в режиме холостого хода (рис.1.8):

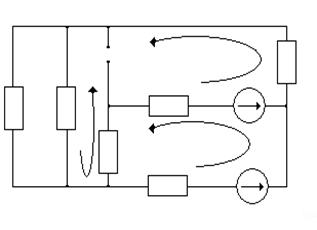
                                       I1    I4              IK2             R7  I7

                                                                     I5     

                                                                                     E1,r01

                            R1     R4                            

                                                               I3

                                                  IK3                    IK1

                                                             R3 I6              

                                             

                                                                      R6 E2,rO2   

Рис.1.8

Используем метод контурных токов:

Для I контура: E₂-E₁=I_K1(R₆+r₀₂+r₀₁+R₅+R₃)-I_K2(R₅+r₀₁)-I_K3R₃;

Для II контура: E₁=I_K2(R₇+R₅+r₀₁)-I_K1(R₅+r₀₁);

Для III контура: 0=I_k3(R₄+R₃)-I_K3R₃;

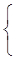10=121I_K1-46I_K2-22I_K3;

=101I_K2-46I_K1;

0=55I_K3-22I_K1;     => I_K1=55I_K3/22;

10=280,5I_K3-46I_K2; => I_K2=(280,5I_K3-10)/46;

30=615,88043I_K3-21,95652-115I_K3; => 

I_K3=0,10391 A.;

I_K2=0,41623 A.;

I_K1=0,25978 A.;

Истинные токи:

I ₅=I_k2-I₁=0,156455 A.;

I₇=I_K2=0,41623 A.;

I₃=I_K1-I_K3=0,155865 A.;

I ₄=I_K3=0,10391 A.;

Находим эквивалентное сопротивление данной электрической цепи:

R143=(R1R3R4) /(R1+R3+R4) =11616/71=163,60563 Om.;

R143602=R143+R6+r02=216,60563 Om.;

R143602501=(R143602(R5+r01))

/(R143602+R5+r01) =9963,85898/262,60563=37,94229 Om.;

RЭКВ. =R7+R1-6=92,94229 Om.;

Рассмотрим III контур (рис.1.9):

 

                         

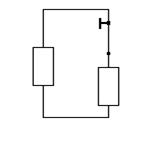
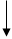                      a        φ_a=φ_b+I₃R₃+I₄R₄;

           I₄   b        φ_a-φ_b=I₃R₃+I₄R₄;

R₄                                                  U_ab= φ_a-φ_b=3,42903+3,42903=6,85806 B.;

               I₃       R₃         

                                     I₂=U_ab/R₂+R_ЭКВ=6,85806/119,94229=0,05718 A.;

Рис.1.9